Вища математика

x – x1	=	y – y1	(10)
x2 – x1		y2 – y1

ПРИКЛАД

Підприємство мало доходи в 2010 році — 2 млн. грн., в 2011 р.

— 2,4 млн. грн. Припускаючи, що розвиток підприємства додержується лінійного закону, спрогнозувати його дохід у 2012 р.

2.2.2. КУТ МІЖ ДВОМА ПРЯМИМИ

Нехай прямі задано рівняннями:

A1x + B1y + C1 = 0, A2x + B2y + C2 = 0.

Тоді кут ϕ між ними можна знайти з формули

cos ϕ =		A1A2 + B1 B2
									.
		2	2			2	2
		A	+ B			A	+ B
		1	1			2	2

Нехай тепер прямі задано рівняннями:

31

y = k1 x + b1, y = k2 x + b2.

Тоді кут ϕ між ними можна знаходиться з формули

tg ϕ = k2 – k1 . 1 + k1 k2

Запишемо умови паралельності та перпендикулярності двох прямих. Якщо прямі задано загальними рівняннями, то ці прямі паралельні при

A1 = B1,

A2 B2

і перпендикулярні при

A1 A2 + B1 B2 = 0.

Якщо ж прямі задано рівняннями з кутовими коефіцієнтами, то ці прямі паралельні при

k1 = k2,

і перпендикулярні при

k1 k2 = –1.

32

2.2.3. ВІДСТАНЬ ВІД ТОЧКИ ДО ПРЯМОЇ

Нехай пряму задано рівнянням

A x + B y + C = 0,

і маємо точку M(x0,y0). Тоді відстань від точки M до прямої дорівнює

d =		A x0	+ By0	+ C			.
			A2 + B2

2.2.4. ТОЧКА ПЕРЕТИНУ ДВОХ ПРЯМИХ

Точка M(x0,y0) перетину двох прямих має належати одночасно двом прямим, тобто:

A x			+ B y		+ C		= 0
	1	0	1	0		1
							= 0.
A x		0	+ B y	0	+ C	2
	2		2

Ця система двох алгебраїчних рівнянь відносно x0,y0 розв’язується одним з відомих способів.

33

2.3. КРИВІ ДРУГОГО ПОРЯДКУ

Визначення

Кривою другого порядку на площині x0y називається крива, задана рівнянням

a11 x2 + a22 y2 + 2a12 x y + a10 x + a20 y + a00 = 0,

де хоча б одне з чисел a11, a12, a22 відмінне від нуля.

Визначення

Еліпсом називається геометричне місто точок на площині, сума відстаней кожної з яких від двох заданих точок (фокусів, на мал.3 —

F1 та F2) є сталою величиною.

My

F1

F2

x

Мал. 3

Позначимо 2a і 2b відповідно довжину частин осей абсцис та ординат, які знаходяться в еліпсі. Тоді a і b називаються відповідно

великою та малою напівосями еліпса.

Канонічне рівняння еліпса має вигляд:

34

2	2
x2	+ y2 = 1.
a	b

Для характеристики еліпса вводять так званий ексцентриситет

ε, який характеризує степінь відхилення еліпса від кола, тобто степінь витягну тості еліпса:

2

ε = 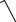1 – ba2 .

Для кола ε = 0, для еліпса 0 < ε < 1.

Визначення

Гіперболою називається геометричне місто точок на площині, модуль різниці відстаней кожної з яких до двох заданих точок (фокусів) є сталою величиною.

y

M

F1		F2	x

Мал. 4

35

Канонічне рівняння гіперболи має вигляд:

2	2
x2	– y2 = 1,
a	b

де a і b — відповідно дійсна та уявна півосі гіперболи. На малюнку Рис. 4: a — довжина відрізку, що з’єднає початок координат з точкою перетину гіперболи і осі абсцис.

Ексцентриситетом гіперболи називається ε		2	> 1 .
	= 1 + b2
		a

Прямі y = ± aε x називаються асимптотами гіперболи.

Визначення

Параболою називається геометричне місто точок площини, рівновіддалених від фіксованої точки F (фокуса) та фіксованої прямої d

(директриси), що не проходить через точку F.

y

y2 = 2px

B

M x

F

A

d

Мал. 5

36

Позначимо відстань між фокусом і директрисою через p. Тоді канонічне рівняння параболи має вигляд:

y2 = 2px.

2.4. АНАЛІТИЧНА ГЕОМЕТРІЯ У ПРОСТОРІ

2.4.1. ПЛОЩИНА У ПРОСТОРІ

Розглянемо спочатку загальне рівняння площини у просторі:

A x + B y + C z + D = 0,

де A, B, C, D — довільні числа, причому хоча б одне з перших трьох відмінне від нуля.

Сформулюємо умови паралельності та перпендикулярності двох площин.

Дві площини:

A1x + B1y + C1z + D1 = 0 і A2x + B2y + C2z + D2 = 0

перпендикулярні тоді й тільки тоді, коли

37

A1 A2 + B1 B2 + C1 C2 = 0.

Дві площини:

A1x + B1y + C1z + D1 = 0 і A2x + B2y + C2z + D2 = 0

паралельні тоді й тільки тоді, коли

A1 = B1 = C1,

A2 B2 C2

тобто у паралельних площин коефіцієнти при відповідних координатах пропорційні.

2.4.2. ПРЯМА У ПРОСТОРІ

Розглянемо дві непаралельні площини у просторі. Вони перетинаються по прямій лінії. Отже, загальне рівняння прямої у тривимірному просторі має вигляд:

A1x + B1y + C1z + D1 = 0

.

A2x + B2y + C2z + D2 = 0

Нехай тепер відомо, що пряма проходить через точку M0(x0,y0,z0) паралельно напрямному вектору s(m,n,p). Складемо рівняння прямої у цьому випадку. Візьмемо на прямій довільну точку M(x,y,z). Вектори s(m,n,p) і M0M = (x – x0, y – y0, z – z0) паралельні, тому:

38

x –mx0 = y –ny0 = z –pz0 .

Це рівняння називається канонічним рівнянням прямої у тривимір-

ному просторі.

39

3. МАТЕМАТИЧНИЙ АНАЛІЗ

Введемо поняття квантора. У математичному аналізі у твердженнях застосовуються два квантори: — „для всіх”, „для кожного”, — „існує”, „знайдеться хоча б одне”. Тепер, наприклад твердження „для кожного значення a < 0 знайдеться хоча б одне b > 0” можна записати таким чином: „a < 0 b > 0”.

3.1. ГРАНИЦІ ПОСЛІДОВНОСТІ ТА ФУНКЦІЇ

3.1.1. ГРАНИЦІ ПОСЛІДОВНОСТІ

Визначення

Якщо кожному натуральному числу за певним законом поставлена у відповідність деяка величина, то говорять, що множина останніх утворює послідовність і пишуть {xn} = x1,x2,…,xn,… Величини x1,x2,…,xn,… називають членами послідовності, а xn — загальним членом.

Приклади
Послідовності: 1) {xn}=	1,	2) {xn}=	(–1)n	, 3) xn+1=xn+d, 4) xn+1=xn q.
	n		n
40