Вища математика

Теорема про похідну складної функції

Якщо функція y = f(u) має похідну у точці u, а функція u = ϕ(x) — похідну у точці x, то складна функція y = f(ϕ(x)) має похідну у точці

x, причому y′ = y′u′.

x u x

Визначення

Похідною другого порядку y′′ функції y = f(x) називається похідна від першої похідної функції y = f(x).

Наприклад, (x2)′′ = (2x)′ = 2.

Східним чином можна визначити похідну функції y = f(x) будьякого натурального порядку, більшого за 2.

3.3. ДИФЕРЕНЦІАЛ ФУНКЦІЇ

Із визначення похідної функції випливає, що якщо функція є диференційованою на відрізку [a;b], то її приріст можна записати у вигляді:

y = f ′(x) x + α( x) x,

61

де α( x) є нескінченою малою при x → 0.

Визначення

Головна частина приросту функції y = f(x) при фіксованому x = x0

називається диференціалом функції y = f(x) і позначається dy = f ′(x) x.

Геометричний зміст диференціала dy легко усвідомити з малюнка 8:

Мал. 8
Оскільки y ≈ dy при малих x, то f(x0 +	x) ≈ f(x0) + f ′(x0)	x. Ця
формула дає змогу знаходити наближені	значення f(x0 + x)	при
малих x, коли відомі f(x0) і f ′(x0).
Приклад
62

Знайти наближене значення 0,98.

Розв’язок. Позначимо x = 0,98, f(x) = 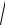x. Виберемо число x0 = 1 так, щоб, по-перше x = 0,98 – 1 = –0,02 було б достатньо малим, а, по-друге, легко можна було б підрахувати f(x0) і f ′(x0).

f(x0) = f(1) = 1. f ′(x) = 21x , f ′(x0) = f ′(1) = 12.

Тоді f(x0 + x) = 0,98 ≈ f(x0) + f ′(x0) x = 1 + 12 (–0,02) = 9,99.

3.4. ТЕОРЕМИ ПРО ДИФЕРЕНЦІЙОВАНІ ФУНКЦІЇ

Визначення

Функція y = f(x) називається зростаючою (спадаючою) в точці x = x0, якщо існує такий окіл точці x = x0, в якій f(x) > f(x0) при x > x0 (x < x0) і f(x) < f(x0) при x < x0 (x > x0).

Теорема (достатня умова монотонності в точці)

Якщо функція y = f(x) диференційована в точці x = x0 і f ′(x0) > 0 (f ′(x0) < 0), то функція зростає (спадає) в точці x = x0.

63

Визначення

Функція y = f(x) називається зростаючою (спадаючою) на проміжку <a;b>, якщо x1,x2 <a;b> із умови x2 > x1 випливає

f(x2) > f(x1) (f(x2) < f(x1)).

Теорема (достатня умова монотонності)

Якщо f ′(x) > 0 (f ′(x) < 0) x <a;b>, то функція зростає (спадає) на

<a;b>.

Визначення

Функція y = f(x) в точці x = a має максимум (мінімум), якщо існує такий окіл точці x = a, в якому f(x) < f(a) (f(x) > f(a)). Максимум і мінімум з’єднаються загальною назвою екстремум.

Теорема (необхідна умова екстремуму)

Якщо функція y = f(x) має в точці x = a екстремум, то f ′(x) = 0 або не існує.

64

Теорема (перша достатня умова екстремуму)

Нехай функція y = f(x) має похідну в точці x = a і деякому її околі. Тоді, якщо при проході через точку x = a похідна f ′(x) змінює знак з плюса на мінус (мінуса на плюс) то x = a — точка максимуму (мінімуму).

3.5. АСИМПТОТИ

Визначення

Пряма x = a називається вертикальною асимптотою графіка функції

y = f(x), якщо хоча б одна з границь lim f(x) або lim f(x) дорівнює ∞.

x→a–0 x→a+0

Визначення

Пряма y = k x + b називається похилою асимптотою графіка функції y = f(x) при x → +∞, якщо f(x) = k x + b + α, де α → 0 при x → +∞.

Теорема

Для того, щоб пряма y = k x + b була похилою асимптотою графіка функції y = f(x) при x → +∞, необхідно і достатньо, щоб існували

границі: lim f(x)	= k,	lim	f(x) – k x	)	= b.
x→+∞ x		x→+∞(

65

3.6. ПРАВИЛО ЛОПІТАЛЯ

Теорема

Якщо 1) f (x) і g (x) визначені і диференційовані в околі точки x = a;

2) lim f (x) = lim g (x) = 0;

x→a x→a

3) g′(x) ≠ 0 в околі точки x = a;

4) lim f ′′((x)),

x→a g x

то lim f (x)	= lim f ′(x) .
x→a g(x)	x→a g′(x)

Зауваження

Аналогічні теореми мають місце в умовах, коли

1) lim f (x) = lim g(x) = ∞;

x→a x→a

2) lim f (x) = lim g(x) = 0;

x→∞ x→∞

3) lim f (x) = lim g(x) = ∞.

x→∞ x→∞

3.7. СХЕМА ПОБУДОВИ ГРАФІКА ФУНКЦІЇ

66

3.7.1. СХЕМА

1. Потрібно знайти область визначення D(f) функції y = f(x) і значення цієї функції в точках розриву й граничних точок області визначення.

2. Якщо в точці х = с функція y = f(x) має розрив, причому lim f(x) = ∞,

x→c

то х = с — вертикальна асимптота графіка функції y = f(x).

Якщо функція визначена на півпрямій або на всій числовій прямій, то варто встановити, чи має графік функції похилі асимптоти.

3. Установити, чи є функція парною, непарною, періодичною.

Якщо функція періодична, то досить провести дослідження функції на будь-якому відрізку, довжина якого дорівнює періоду функції, а потім, побудувавши графік на цьому відрізку, поширити його на всю область визначення функції.

4. Знайти нулі функції, тобто вирішити рівняння f(х) = 0. Ці корені й точки розриву функції розбивають її область визначення на проміжки сталого знаку функції.

5. Знайти похідну y′ = f ′(x) і з її допомогою знайти екстремуми і проміжки зростання й спадання функції.

6. Знайти проміжки збереження напряму опуклості й точки перегину графіка функції.

7. Побудувати ескіз графіка.

67

3.7.2. ПРИКЛАД

Приклад

Побудувати графік функції y = arcsin 1 2+xx2 .

1. Функція визначена при тих значеннях х, для яких, як витікає з

визначення функції арксинуса, виконується нерівність		2x		≤ 1.
		1 + x2

Воно рівносильне нерівності (1 – |х|)2 ≥ 0. Остання нерівність є вірною

для будь-яких дійсних х. Отже, D(f) = R. Функція 1 2+xx2 неперервна в

будь-якій точці (як частка двох безперервних функцій). Тому функція

arcsin		2x	— також неперервна в будь-якій точці R.
	1	+ x2
2. Оскільки функція arcsin				2x	неперервна в будь-якій точці, то
				1 + x2

графік функції не має вертикальних асимптот. Для знаходження похилої асимптоти обчислимо наступні границі:

lim	f(х)	=	lim 1arcsin			2x			= 0 = k,
					1 + x			2
x→+∞ х			x→+∞ х
lim [ f(х) – k x] =			lim arcsin	2x			= arcsin 0 = 0 = b.
				1 + x		2
x→+∞			x→+∞

Звідси випливає, що пряма y = 0 є асимптотою графіка функції при x → +∞. Аналогічно можна встановити, що та ж пряма y = 0 є асимптотою графіка функції при x → –∞.

68

3.Очевидно, що функція — неперіодична і є непарною. Тому замість всієї області визначення D(f) досить розглянути півпряму [0, +∞).

4.Маємо y = 0 при x = 0. Інших нулів, а також точок розриву функція не має. На півпрямій (0, +∞) функція є додатною.

5.Знайдемо точки можливого екстремуму на півпрямій [0,+∞). Обчислимо похідну функції при х ≠ 1:

y′ =			1			2 (1 + x2) – 4x2		2 sign(1 – x2)
						(1 + x2)2	=	1 + x2	.
		1 –		4x2
				(1 + x2)2

Звідси видно, що похідна не дорівнює нулю у жодній точці. У точці х = 1 похідна не існує, тому що у′(1+0) = –1, у′(1–0) = 1. Знак похідної при переході через точку х = 1 змінюється із плюса на мінус. Тому в точці х = 1 функція має максимум, причому у(1) = arcsin 1 = π/2. Відзначимо, що в точці х = 1 функція неперервна, а її похідна має розрив першого роду. У такому випадку відповідна точка графіка [у даному прикладі — точка (1; π/2)] називається кутовою точкою. Проміжки монотонності функції визначаються знаком похідної: у′ > 0 при 0 < х < 1, у′ < 0 при х > 1.

6°. Оскільки друга похідна

у′′ =	–4x sign(1 – x2)	, х ≠ 1
	(1 + x2)2

69

дорівнює нулю лише при х = 0 і у′′ при переході через точку х = 0 міняє знак, то в точці (0; y(0)) = (0; 0) графік функції має перегин. Напрямок опуклості визначається знаком другої похідної: y′′ < 0 при 0 ≤ x < 1, y′′ > 0 при х > 1.

Дослідження функції закінчено.

Тепер будуємо графік функції на проміжку [0; +∞). На відрізку [0; 1]: а) функція зростає від значення y = 0 при x = 0 до значення y = π/2 при

х = 1; б) опуклість спрямована нагору. Далі, на півпрямій [1; +∞): а) функція спадає, залишаючись додатною; б) опуклість спрямована вниз; в) при x →+∞ графік наближається до асимптоти — осі 0х. Відзначимо, що при переході через точку х = 1 змінюється напрямок опуклості графіка, але точка (1; π/2) не є точкою перегину — це

кутова точка:

Нарешті, використовуючи непарність функції, добудовуємо її графік на всій області визначення:

70