4.5. Зависимости между моментами инерции при повороте осей. Главные оси и главные моменты инерции. Радиус инерции сечения

Вычислим моменты инерции фигуры произвольной формы относительно осей, повернутых относительно заданных осей ина угол(Рис.4.14)

Рис.4.14

Пусть моменты инерции относительно осей иизвестны. Выберем произвольную площадкуи выразим ее координаты в системе осейичерез координаты в прежних осяхи:

,. (4.27)

Найдем осевые и центробежный моменты инерции фигуры относительно повернутых осей и:

. (4.28)

Принимая во внимание, что

;и,

получим:

. (4.28)

Таким же образом установим:

. (4.29)

Центробежный момент инерции принимает вид:

или

. (4.30)

Выразим осевые моменты через синус и косинус двойного угла. Для этого введем следующие функции:

. (4.31)

Подставляя (4.31) в формулы (4.27) и (4.28), получим:

. (4.32)

. (4.33)

Если сложить выражения для осевых моментов инерции (4.32) и (4.33), то получим:

. (4.34)

Условие (4.34) представляет условие инвариантности суммы осевых моментов инерции относительно двух взаимно перпендикулярных осей, т.е. сумма осевых моментов инерции относительно двух взаимно перпендикулярных осей не зависит от величины угла поворота осей и является величиной постоянной.Ранее это условие было получено на том основании, что сумма осевых моментов инерции относительно двух взаимно перпендикулярных осей равнялась величине полярного момента инерции относительно точки пересечения этих осей.

Исследуем уравнение для момента инерции на экстремум и найдем такое значение угла, при котором момент инерции достигнет экстремальной величины. Для этого возьмем первую производную от момента инерциипо углу(выражение (4.32)) и результат приравняем нулю. При этом положим.

(4.35)

Выражение в скобках представляет собой центробежный момент инерции относительно осей, наклоненных к оси под углом. Относительно этих осей центробежный момент инерции равен нулю:

, (4.36)

а это означает, что новые оси являются главными осями.

Ранее было определено, что главными осями инерции являются оси, относительно которых центробежный момент инерции равен нулю. Сейчас это определение можно расширить – это оси, относительно которых осевые моменты инерции имеют экстремальные значения. Моменты инерции относительно этих осей называютсяглавными моментами инерции.

Найдем положение главных осей инерции. Из выражения (4.36) можно получить:

. (4.37)

Полученная формула дает для угла два значения:и.

Следовательно, существуют две взаимно перпендикулярные оси, относительно которых моменты инерции имеют экстремальные значения. Как уже отмечалось выше, такие оси называются главными осями инерции. Остается установить, относительно какой из осей момент инерции достигает максимального значения, а относительно какой – минимального значения. Решить эту задачу можно путем исследования второй производной от выражения (4.32) по углу . Подставив в выражение для второй производной значение углаилии исследуя знак второй производной, можно судить о том, какой из углов соответствует максимальному моменту инерции, какой – минимальному. Ниже будут приведены формулы, которые дадут однозначное значение угла.

Найдем экстремальные значения для моментов инерции. Для этого преобразуем выражение (4.32) , вынося за скобку :

. (4.38)

Используем известную из тригонометрии функцию и подставим в нее выражение (4.37), получим:

. (4.39)

Подставляя в формулу (4.38) выражение (4.39) и производя необходимые вычисления, получаем два выражения для экстремальных моментов инерции, которые не включают в себя угол наклона осей :

; (4.40)

. (4.41)

Из формул (4.40) и (4.41) видно, что величины главных моментов инерции определяются непосредственно через моменты инерции относительно осей и. Поэтому их можно определять, не зная положения самих главных осей.

Зная экстремальные значения моментов инерции иможно помимо формулы (4.37) определять положение главных осей инерции.

Приведем без вывода формулы, позволяющие находить углы имежду осьюи главными осями:

;(4.42)

Угол определяет положение оси, относительно которой момент инерции достигает максимальной величины (), уголопределяет положение оси, относительно которой момент инерции достигает минимальной величины ().

Введем еще одну геометрическую характеристику, которая называется радиусом инерции сечения. Обозначается эта характеристика буквой и может быть вычислена относительно осейиследующим образом:

;(4.43)

Радиус инерции находит широкое применение в задачах сопротивления материалов и его применение будет рассмотрено в следующих разделах курса.

Рассмотрим несколько примеров расчетов конструкций с учетом поворота осей и с использованием радиуса инерции сечения.

Пример 4.7. Моменты инерции сечения прямоугольной формы относительно главных осей равны соответственносм⁴,см⁴. При повороте на 45⁰моменты инерции относительно новых осей оказались одинаковыми. Чему равна их величина?

Решение:

Для решения задачи воспользуемся выражением (4.28) с учетом того, что центробежный момент инерции относительно главных осей равен нулю:

. (а)

Подставим в формулу (а) численные значения для моментов инерции и угла поворота осей:

см⁴.

Пример 4.8. У которой из фигур (Рис.4.15), имеющих одинаковую площадь, радиус инерции относительно оси , будет наибольшим? Определить наибольший радиус инерции сечения относительно оси .

Решение:

1. Найдем площадь каждой из фигур и размеры сечений. Площадь фигур равняется для третьей фигуры см².

Диаметр первого сечения найдем из выражения:

см.

Размер стороны квадрата:

см.

Основание треугольника:

см.

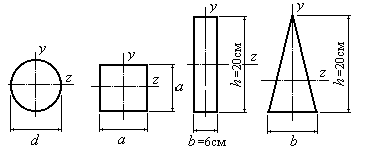
Рис.4.15

2. Находим моменты и радиусы инерции каждого из сечений относительно центральной оси .

Для сечения круглой формы:

см⁴;см.

Для сечения квадратной формы:

см⁴;см.

Для сечения прямоугольной формы:

;

Для сечения треугольной формы:

см⁴;см.

Наибольший радиус инерции оказался у сечения прямоугольной формы и равен он см.