
- •Тема 3 основи теорії напруженого і деформованого стану
- •3.2. Лінійний напружений стан в більшості випадків цей вид напруженого стану виникає в стержнях при розтяганні або стисканні.
- •3.3.Плоский напружений стан
- •3.3.1. Виведення формул для напружень на похилих площадках
- •3.3.2. Обчислення величин головних напружень і визначення положення головних площадок
- •3.3.3. Екстремальні дотичні напруження
- •3.3.4. Приклади дослідження плоского напруженого стану в точці
- •3.4. Об'ємний напружений стан
- •3.4.1. Поняття про тензор напружень. Екстремальні дотичні напруження
- •3.4.2. Напруження на довільно нахилених площадках
- •3.4.3. Октаедричні напруження. Поняття про інтенсивність напружень
- •3.5. Деформований стан у точці
- •3.5.1. Поняття про тензор і девіатор тензора деформацій. Головні лінійні деформації
- •3.5.2. Закон Гука при плоскому та об'ємному напружених станах
- •3.5.3.Об'ємна деформація. Об'ємний закон Гука
- •3.6. Тести до теми №3 “Основи теорії напруженого та деформованого стану” Таблиця 3.1
3.2. Лінійний напружений стан в більшості випадків цей вид напруженого стану виникає в стержнях при розтяганні або стисканні.
Розглянемо
стержень, який зазнає простого розтягання
(Рис.3.5,а). Обчислимо напруження, які
діють у будь-якому похилому перерізі.
Розсічемо стержень перерізом
![]() ,
що складає кут
,
що складає кут![]() з поперечним перерізом
з поперечним перерізом![]() ,
перепендикулярним до осі стержня. Цей
самий кут складають між собою і нормалі
до поперчного і похилого перерізів. За
додатний напрямок відліку кута
,
перепендикулярним до осі стержня. Цей
самий кут складають між собою і нормалі
до поперчного і похилого перерізів. За
додатний напрямок відліку кута![]() приймемо напрямок проти годинникової
стрілки. Нормаль ОА, спрямовану назовні
стосовно відсіченої частини стержня,
будемо називати зовнішньою нормаллю
приймемо напрямок проти годинникової
стрілки. Нормаль ОА, спрямовану назовні
стосовно відсіченої частини стержня,
будемо називати зовнішньою нормаллю![]() до перерізу
до перерізу![]() .
Площу перерізу
.
Площу перерізу![]() позначимо
позначимо![]() ,
площу перерізу
,
площу перерізу![]() позначимо
позначимо![]() .
.
Відкинемо
верхню частину стержня і замінимо дію
її на нижню частину напруженнями
![]() (Рис.3.5,б).
(Рис.3.5,б).

Рис.3.5
Приймаючи
гіпотезу плоских перерізів, будемо
вважати, що напруження
![]() рівномірно розподілені по площі
рівномірно розподілені по площі![]() :
:
![]() .
(3.1)
.
(3.1)
З
огляду на те, що
![]() і підставляючи
і підставляючи![]() в
(3.1), одержимо:
в
(3.1), одержимо:
![]() ,
(3.2)
,
(3.2)
де
![]()
нормальне напруження на площадці
нормальне напруження на площадці
![]() ,
перпендикулярній до розтягальної сили.
,
перпендикулярній до розтягальної сили.
Проектуючи
![]() на нормаль
на нормаль![]() і на площину перерізу, одержимо вираз
для нормальних і дотичних напружень на
похилій площадці:
і на площину перерізу, одержимо вираз
для нормальних і дотичних напружень на
похилій площадці:
![]() ;
;
![]()
або
![]() ,
(3.3)
,
(3.3)
![]() .
(3.4)
.
(3.4)
Як
видно з формул (3.3)(3.4),
при
![]()
![]() ,
,![]() ;
при
;
при![]() напруження
напруження![]() і
і![]()
![]() дорівнюють
нулю (Рис.3.6).
дорівнюють
нулю (Рис.3.6).

Рис.3.6
Таким чином, при простому розтяганні і стисканні у кожній точці стержня нормалі до головних площадок перпендикулярні та паралельні поздовжній осі стержня, а головні напруження в них відповідно дорівнюють:
![]() ;
;
![]()
при розтяганні,
при розтяганні,
![]() ;
;
![]()
при стисканні.
при стисканні.
Максимальні
дотичні напруження діють у площадках,
нахилених до головних площадок під
кутом
![]() .
При цьому
.
При цьому
![]() (3.5)
(3.5)
Приклад 3.1. Визначити нормальні і дотичні напруження на похилих площадках для елементів, наведених на рис.3.7.

Рис.3.7
Розв’язок:
Для елемента на рис.3.7,а:
 МПа;
МПа;
 ;
; .
.
Звідки:
![]() МПа;
МПа;![]() МПа.
МПа.
Для елемента на рис.3.7,б:
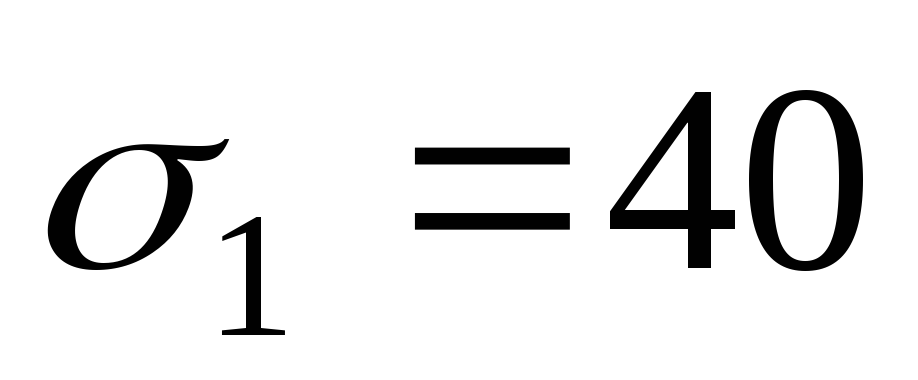 МПа;
МПа;
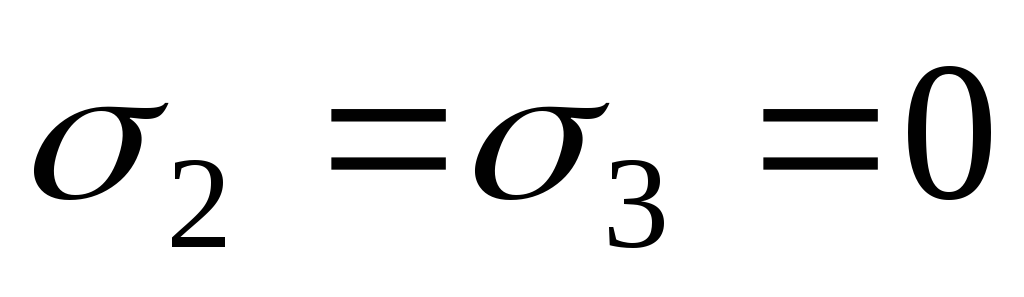 ;
; .
.
Звідки:
![]() МПа;
МПа;![]() МПа.
МПа.
3.
Для елемента на рис.3.7,в:
![]() ;
;
![]() МПа;
МПа;
![]() .
.
Звідки:
![]() МПа;
МПа;![]() МПа.
МПа.
3.3.Плоский напружений стан
Найбільш часто в задачах опору матеріалів зустрічається плоский напружений стан: при крученні, згинанні, згинанні з крученням та ін. Зупинимося на ньому докладніше.
3.3.1. Виведення формул для напружень на похилих площадках
Виділимо
з тіла паралелепіпед (Рис.3.8). Під дією
сил, прикладених до його граней,
паралелепіпед перебуває у рівновазі.
Довжини ребер паралелепіпеда вважаємо
нескінченно малими. Позначимо їх
![]() .
.
Розглянемо
похилі площадки, перпендикулярні
незавантаженим граням паралелепіпеда.
Розріжемо елементарний паралелепіпед,
зображений на рис. 3.8, похилим перерізом,
перпендикулярним площині
![]() ,
виділивши з нього елементарну трикутну
призму (Рис.3.9).
,
виділивши з нього елементарну трикутну
призму (Рис.3.9).

Рис.3.8
Нахил
площадки з шуканими напруженнями будемо
визначати кутом
![]() ,
що утворює зовнішня нормаль до цієї
площадки з віссю
,
що утворює зовнішня нормаль до цієї
площадки з віссю![]() .
З рис.3.9 випливає, що
.
З рис.3.9 випливає, що
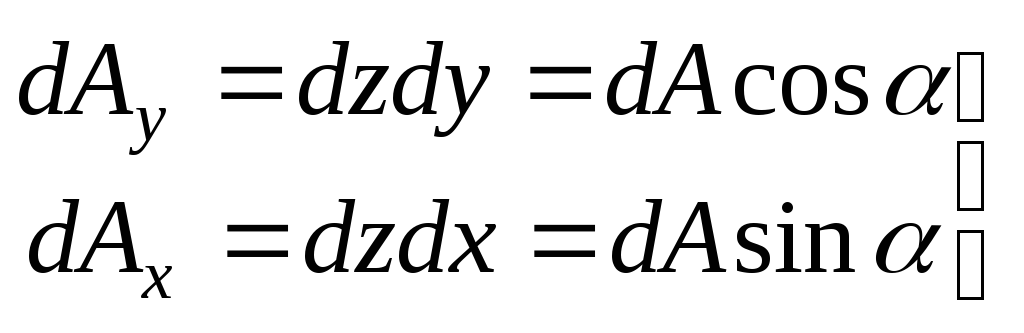
![]() (3.6)
(3.6)

Рис.3.9
Система сил, що наведена на рис.3.9, є плоскою довільною системою. Рівновага такої системи сил описується трьома незалежними рівняннями. Складемо ці рівняння.
![]() .
(3.7)
.
(3.7)
Звідки:
![]() .
(3.8)
.
(3.8)
Вираз (3.8) являє собою закон парності дотичних напружень: дотичні напруження, що діють на двох будь-яких взаємно перпендикулярних площадках, рівні за величиною і протилежні за знаком.
При плоскому напруженому стані можливі лише два варіанти дії дотичних напружень (Рис.3.10).

Рис.3.10
Для
визначення напружень на похилій площадці
спроектуємо сили, що діють на призму
(Рис.3.9), на осі
![]() і
і![]() .
Одержимо:
.
Одержимо:
![]() ;
(3.9)
;
(3.9)
![]() (3.10)
(3.10)
Підставляючи
в (3.9)(3.10)
замість
![]() і
і![]() з виразу (3.6), скоротимо всі доданки на
з виразу (3.6), скоротимо всі доданки на![]() .
Далі, з огляду на те, що згідно до (3.8)
.
Далі, з огляду на те, що згідно до (3.8)![]() ,
а
,
а![]() і
і![]() ,
знаходимо:
,
знаходимо:
![]() (3.11)
(3.11)
![]() (3.12)
(3.12)
Надамо формулу (3.9) у трохи іншому вигляді, використовуючи відомі з тригонометрії рівності:
 (3.13)
(3.13)
Підставляючи (3.13) у (3.11), одержимо:
![]() (3.14)
(3.14)
З'ясуємо зв'язок між нормальними
напруженнями
![]() і
і![]() ,
що діють у двох взаємно перпендикулярних
площадках (Рис.3.11).
,
що діють у двох взаємно перпендикулярних
площадках (Рис.3.11).

Рис.3.11
Напруження
![]() визначається за формулою (3.14). Напруження
визначається за формулою (3.14). Напруження![]() одержимо, якщо в цю формулу підставимо
одержимо, якщо в цю формулу підставимо![]() :
:
![]()
або
![]() .
(3.15)
.
(3.15)
Складаючи (3.14) і (3.15), маємо:
![]() (3.16)
(3.16)
Вираз (3.16) одержав назву умови інваріантості суми нормальних напружень, що діють на двох взаємно перпендикулярних площадках: у даній точці алгебраїчна сума нормальних напружень для будь-яких двох взаємно перпендикулярних площадок є величиною сталою. Цю умову використовують для перевірки правильності розв’язання задач при дослідженні напруженого стану у точці.
