
- •Министерство образования и науки Украины
- •С о д е р ж а н и е
- •В в е д е н и е
- •I. П о н я т и е и н т е г р а л а
- •1.1. Неопределенный интеграл.
- •Основные свойства неопределенного интеграла
- •Основные свойства неопределенного интеграла
- •Определенный интеграл. Формула Ньюбона-Лейбница. Основные свойства определенного интеграла
- •Формула Ньютона-Лейбница
- •Основные свойства определенного интеграла
- •II. М е т о д ы и н т е г р и р о в а н и я
- •2.1. Метод непосредственного интегрирования
- •2.2. Метод замены переменной
- •2.3. Интегрирование по частям
- •2.4. Интегрирование рациональных дробей
- •2.5. Интегрирование некоторых иррациональных функций
- •2.6. Интегрирование тригонометрических функций
- •Примеры.
- •6) Случай универсальной подстановки .
- •2.7. Несобственные интегралы
- •Ііі. Задания для индивидуального решения
- •3.1. Метод непосредственного интегрирования
- •3.2. Метод замены переменной
- •3.3. Метод интегрирования по частям
- •3.4. Интегрирование рациональных дробей
- •3.5. Интегрирование иррациональных функций
- •3.6. Интегрирование тригонометрических функций
- •Несобственные интегралы
2.5. Интегрирование некоторых иррациональных функций
Главная идея при интегрировании иррациональных функций заключается в том, чтобы различными преобразованиями свести данный интеграл к интегралу от известных рациональных функций.
Если подынтегральное выражение содержит линейную иррациональность типа
 ,
то целесообразна подстановка:
,
то целесообразна подстановка:
 .
.
Например.
 .
.
Подкоренное выражение заменяют переменной в такой степени, чтобы корень извлекался. Если имеется несколько корней с разными показателями и одинаковыми подкоренными выражениями, то вводится такая замена, чтобы все корни извлекались (общий знаменатель всех дробных показателей).
Например.
1.

![]() .
.
![]() 2.
2.

![]()
![]() .
.
Замечание.
Если функция содержит выражения
![]() ,
то, чтобы свести ее к рациональному
виду, вводят
,
то, чтобы свести ее к рациональному
виду, вводят
![]() .
.
Подынтегральное выражение имеет вид дифференциального бинома
 .
.
При вычислении таких интегралов руководствуются следующим:
а)
если![]() - целое, то раскладывают бином;
- целое, то раскладывают бином;
б)
если
![]() - целое, то делают замену
- целое, то делают замену
![]() ;
;
в)
если
![]() - целое, то делают замену
- целое, то делают замену
![]() .
.
![]() -
знаменатель дроби
-
знаменатель дроби
![]() .
.
Например.

![]()

![]()
 .
.
Интеграл от простейшей квадратичной иррациональности
 вычисляют путем выделения полного
квадрата в знаменателе и замены
переменной и приходят к табличным
интегралам:
вычисляют путем выделения полного
квадрата в знаменателе и замены
переменной и приходят к табличным
интегралам:
 и
и
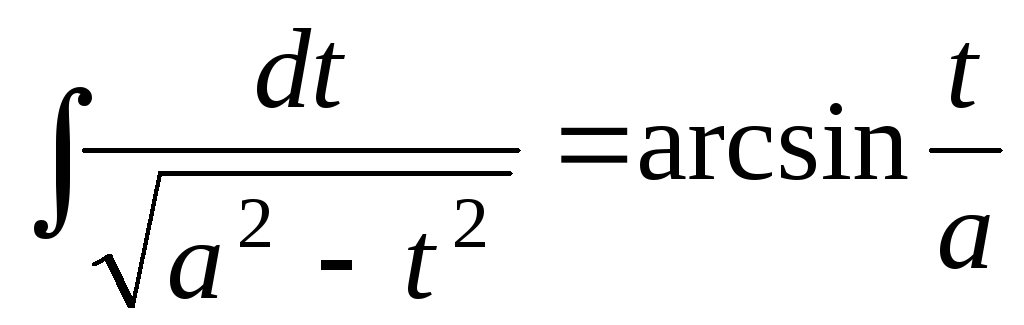 .
.

 .
.
Интеграл от более сложной квадратичной иррациональности
 вычисляют путем выделения под корнем
полного квадрата, замены переменной и
получения суммы двух интегралов: один
вида
вычисляют путем выделения под корнем
полного квадрата, замены переменной и
получения суммы двух интегралов: один
вида
 ,
а другой – вида 3.
,
а другой – вида 3.
Например.


![]() .
.
Если подынтегральная функция имеет вид
 ,
то следует сделать замену
,
то следует сделать замену
 .
.
Например,
![]() .
.
|
|
|
предварительно преобразуем подкоренное выражение:
![]()
![]()


![]()
![]() .
.
Если задан интеграл вида
 ,
то после выделения полного квадрата и
замены переменной используют формулу
интегрирования по частям.
,
то после выделения полного квадрата и
замены переменной используют формулу
интегрирования по частям.
Например,
а)


![]() .
.
Запишем начало и концовку:
![]() .
.
Приведем подобные элементы:
![]() ;
;
![]() .
.
Возвратимся к старым переменным и запишем результат интегрирования:
![]() .
.
б)
![]()

![]()
![]()
![]() .
.
В результате получаем равенство:
![]()
![]() .
.
![]() .
.
Замечание.
Интегралы вида
![]() можно вычислять с помощью подстановки
можно вычислять с помощью подстановки
![]() ,
однако, методом интегрирования по частям
результат достигается быстрее.
,
однако, методом интегрирования по частям
результат достигается быстрее.
Если встречается интеграл вида
 ,
то заменой
,
то заменой
 (или
(или
 )
его преобразуют к более простому виду.
)
его преобразуют к более простому виду.

![]()
 .
.
![]() .
.
2.6. Интегрирование тригонометрических функций
Случай перехода от произведения функций к сумме:
а)
![]() ;
;
б)
![]() ;
;
в)
![]() .
.
В результате применения указанных формул получают табличные интегралы.
Примеры.
а)
![]()
![]() .
.
б)
 .
.
2) Случай, когда имеется произведение степени одной функции на другую:
а)
![]() ,
проводят замену
,
проводят замену
![]() ;
;
б)
![]() ,
проводят замену
,
проводят замену
![]() .
.
Примеры.
а)
 .
.
б)
 .
.
3) Случай четной степени одной функции:
а)
![]() ,
используют формулу
,
используют формулу
![]() ,
,
![]() .
.
б)
![]() ,
используют формулу
,
используют формулу
![]() ,
,
![]() .
.
Указанные формулы позволяют понижать степень.
Примеры.
а)
![]()
![]()
![]()
![]() .
.
б)

 .
.
4) Случай нечетной степени одной функции.
а)
![]() - выделяют один
- выделяют один
![]() ,
остальную часть выражают через
,
остальную часть выражают через
![]() и проводят замену
и проводят замену
![]() .
.
б)
![]() - выделяют один
- выделяют один
![]() ,
остальную часть выражают через
,
остальную часть выражают через
![]() и проводят замену
и проводят замену
![]() .
.
Примеры.
а)
![]()

![]() .
.
б)

![]() .
.
5)
Случай произведения степеней двух
функций:
![]()
а)
![]() – четные – понижают степень (как в п.3);
– четные – понижают степень (как в п.3);
б) хотя бы одно нечетное, тогда решают как в п. 4.
Примеры.
а)

![]()
![]()
![]()

![]()
![]()
![]() .
.
б)



![]() .
.
в)
![]()

![]() .
.

