3. Алгебраїчні лінії першого порядку. Пряма на площині

Пряма на площині фіксується, якщо відомі:

1. точка на прямій і вектор, перпендикулярний до прямої;

2. точка на прямій і вектор, паралельний прямій;

3. точка на прямій і кутовий коефіцієнт прямої;

4. дві точки на прямій.

3.1. Рівняння прямої, що проходить через задану точку перпендикулярно до заданого вектора. Загальне рівняння прямої

Нехай пряма проходить через задану точку М₀(х₀;у₀) перпендикулярно до заданого вектора нормалі(рис. 13). Виберемо на прямій змінну точкуМ(х,у) і запишемо умову перпендикулярності векторіві:

. (13)

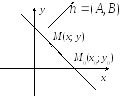
Рис. 13 Рис. 14

Скалярний добуток (13) у координатній формі має вигляд

А(хх₀) +B(yу₀) = 0. (14)

Рівняння (14) називається рівнянням прямої, що проходить через задану точку М₀(х₀;у₀) перпендикулярно до заданого вектора.

Окремі випадки рівняння (14):

1. при x₀=y₀= 0 маємо рівняння прямої, яка проходить через початок координат:

Ах +Ву = 0; (15)

2. при B = 0,A  0 одержуємо рівняннявертикальноїпрямої:х = х₀;

3. при A = 0,B  0 одержуємо рівняннягоризонтальноїпрямої:y = y₀.

З рівняння (14) одержимо загальне рівнянняпрямої

Ах + Ву + D= 0. (16)

З (16) і (11) випливає, що всяка пряма є алгебраїчною лінією першого порядку.

3.2. Рівняння прямої, що проходить через задану точку паралельно заданому вектору

Нехай пряма проходить через задану точку М₀(х_0;у₀) паралельно заданому вектору. Виберемо на прямій змінну точкуМ(х;у). Запишемо умову паралельності векторіві(рис. 14):

. (17)

Рівняння (17) називається рівнянням прямої, що проходить через задану точку М₀(х₀;у₀) паралельно заданому вектору.

3.3. Рівняння прямої, що проходить через дві задані точки

Нехай на прямій задані дві фіксовані точки М₁(х₁; у₁), M₂(х₂; у₂). Виберемо на прямій змінну точку М(х; у) і запишемо умову колінеарності векторів = (x  x_1; y  y₁) і = (x₂  x_1; y₂  y₁) (рис. 15):

(18)

• рівняння прямої, що проходить через дві задані точки М₁(х_1;у₁),M₂(х₂;у₂).

Рис. 15 Рис. 16

3.4. Рівняння прямої у відрізках на осях

Нехай пряма відтинає на координатних осях Ox, Oy відрізкиa,b, що не дорівнюють нулю (рис. 16). Підставляючи в рівняння (18) координати точок перетину прямої з осямиМ₁(a; 0),M₂(0;b), одержуємо рівняння прямої у відрізках на осях:

. (19)

3.5. Рівняння прямої з кутовим коефіцієнтом

Нехай пряма проходить через задану точку М₀(х₀;у₀) і складає з віссюОхкут/2 (рис. 17). Виберемо на прямій змінну точкуМ(х;у) і запишемо співвідношення:

. (20)

Число kназиваєтьсякутовим коефіцієнтом прямої.

Рис. 17

З формули (20) одержуємо рівняння прямої, що проходить через задану точку М₀(х_0;у₀) і має заданий кутовий коефіцієнтk:

(21)

З рівняння (21) при x₀= 0 одержимо рівняння прямої з кутовим коефіцієнтом:

(22)

де b=y₀– відрізок, що відтинається прямою на осіОу(рис. 17).

Зауваження. Загальне рівняння прямої (16), а також рівняння прямої з кутовим коефіцієнтом (22) є “стандартними” формами запису рівнянь прямої, в яких вона задається або до яких зводяться інші рівняння прямої у процесі розв’язання задач.

3.6. Кут між двома прямими

1. прямі задані загальними рівняннями

(23)

Косинус гострого кутаміж прямими:

(24)

2. прямі задані рівняннями з кутовим коефіцієнтом

(25)

Тангенс кута  між прямими (рис. 18):

(26)

Рис. 18

3.7. Умови паралельності й перпендикулярності двох прямих

Умови паралельності прямих, заданих рівняннями (23), (25):

. (27)

Умови перпендикулярності двох прямих:

. (28)

3.8. Нормальне рівняння прямої

Нехай p– відстань від початку координат до прямої. Уведемо одиничний вектор нормалі= (cosα; sin) і змінну точку прямоїМ(x;y). Тоді проекція векторана напрям вектора нормалідорівнює відстанір(рис. 19):

Рис. 19

З останньої рівності одержуємо нормальне рівняння прямої:

(29)

Ознаки нормального рівняння:

1. вільний член від’ємний або дорівнює нулю;

2. коефіцієнти при x,yпо абсолютній величині не перевищують 1;

3. сума квадратів коефіцієнтів при x,yдорівнює 1.

Зведення загального рівняння прямої до нормального вигляду

Зведемо до нормального вигляду загальне рівняння прямої

Ах+Ву+D= 0. (30)

Для цього помножимо його на нормуючий множник μ≠ 0, який підберемо з умов:

(31)

Знак μ вибираємо протилежним знаку вільного члена D:

(32)

Нормальне рівняння:

. (33)

3.9. Відстань від точки до прямої

Знайдемо відстань від точки K(x₁;y₁) до прямої (рис. 20). Для цього обчислимо різницю:

(34)

Рис. 20

Відхилення точки від прямої:

(35)

Якщо точка й початок координат знаходяться з одного боку від прямої, то d< 0, а якщо з різних – тоd> 0.

Відстань від точки K(x₁;y₁) до прямої:

• пряма задана нормальним рівнянням (29)

(36)

• пряма задана загальним рівнянням (16)

. (37)

Приклад 6.Знайти відхилення і відстань від точкиМ₀(1; 2) до прямої

2x3y5 = 0.

Розв’язання. Зведемо рівняння прямої до нормального вигляду. Для цього поділимо рівняння на:



Відхилення точки М₀(1; 2) від прямої:

Оскільки d< 0точкаМ₀(1; 2) і початок координат знаходяться з одного боку від прямої.

Відстань від точки М₀(1; 2) до прямої:

Приклад 7.Скласти рівняння прямої, що проходить через точкиM₁(2; 3) іM₂(3; 5).

Розв’язання.Скористаємося формулою (18):

,, 2(x2) =5(y3);

2x+ 5y19 = 0загальне рівняння прямої. Вектор нормалі= = (2; 5);

рівняння прямої у відрізках на осях(a= 19/2;b==19/5);

рівняння прямої з кутовим коефіцієнтом(k=2/5;b= 19/5).

Приклад 8.Скласти рівняння прямої, що проходить через точкуперпендикулярно до прямоїx+ 2y+ 3 = 0.

Розв’язання.1-й спосіб. Дану пряму представимо у вигляді:(). Рівняння шуканої прямої є:. З умови перпендикулярності прямих маємоk₁k₂=1k₂ = 2. Звідсиy+ 3 = 2(x2)2xy7 = 0.

2-й спосіб. Вектор нормалі до даної прямоїпаралельний шуканій прямій. Рівняння прямої, що проходить через точкупаралельно векторумає вигляд:

Приклад 9.Дані вершини трикутникаA(1; 0),B(5; 4),C(1; 3). Скласти рівняння сторін трикутника, медіани й висоти, проведених із вершиниA.

Розв’язання.

а) рівняння сторін знайдемо як рівняння прямих, що проходять через дві точки:

AB: , x1 =y,xy 1 = 0;

BC: ,x5 = 6(y4),x6y+19 = 0;

CA: ,3(x+ 1) = 2(y3), 3x+ 2y3 = 0;

б) медіану, опущену з вершиниAна сторонуBC, позначимоAM. ТочкаMподіляє сторонуBCнавпіл, тому її координати

,.

Рівняння медіани AM:; 7x2y7 = 0;

в) висоту, опущену з вершиниAна сторонуBC, позначимоAK. ПрямаAKпроходить через точкуA(1; 0) перпендикулярно прямійBC, тобто паралельно вектору. Отже, її рівняння:

Зробимо креслення.

Рис. 21

Приклад 10.Протилежні вершини квадрата лежать у точкахA(2; 3) іC(2; 5). Скласти рівняння сторін і діагоналей квадрата.

Розв’язання.

а) складеморівняння діагоналей. Одна з діагоналей проходить через точкиAіC.

AC:x 2y+ 8 = 0.

Діагональ BDквадрата перпендикулярна до діагоналіACі проходить через її серединуточкуKіз координатами

,

Кутовий коефіцієнт AC:k_AC= 1/2, отже, кутовий коефіцієнтBD:k_BD=k_AC=2. Рівняння діагоналіBD:

yy_K=k_BD(xx_K),y4 =2x, 2x+y4 = 0.

Зробимо креслення;

Рис. 22

б) знаходиморівняння сторін. Нехайk_ABкутовий коефіцієнт сторониAB. Кут DAC позначимо , він дорівнює 45. Оскільки tg = tg45 = 1,k_AC = 1/2, то

k_AD= 3.

Рівняння сторони AD:

,y3 = 3(x+ 2),y= 3x+ 9.

Сторона BC проходить через точку C паралельно AD (k_BC = k_AD =3), її рівняння

,y5 = 3(x2),y= 3x1.

З умови перпендикулярності сторін ABіBCзнаходимоk_AB= =1/k_BC=1/3. СторониDCіABпаралельні, їхні кутові коефіцієнти співпадають:k_DC=k_AB=1/3. Знаходимо рівняння сторінABіDC:

AB: ,x+ 3y7 = 0;

DC: ,x+ 3y17 = 0.