4.5. Гіпербола

Канонічне рівняння гіперболи в декартових координатах:

, (50)

де а – дійсна,

b – уявна півосі гіперболи.

При y= 0:х=а. Точки перетинання з віссюOx(a;0) і (a;0) називаютьсявершинами гіперболи. Прих= 0:у²=b²(гіпербола не перетинає вісьОу). Гіпербола має дві гілки, симетричні щодо осіOу.

Прямі , що проходять через діагоналі прямокутника 2а2b, називаютьсяасимптотами гіперболи.Властивість асимптот: при необмеженому видаленні від початку координат гілки гіперболи наближаються до асимптот, не перетинаючи їх.

Рис. 29. Гіпербола

Точки F₁(c; 0),F₂(c; 0), деназиваютьсяфокусамигіперболи, а відрізкиF₁M,F₂Mїїфокальними радіусами.

Величина ε = с/a називається ексцентриситетом гіперболи ( > 1).

Прямі називаютьсядиректрисами гіперболи.

Основна властивість гіперболи: різниця відстаней від довільної точкиМгіперболи до її фокусів є величина стала, що дорівнює2а.

Зауваження 1. Рівняння гіперболи в параметричній формі має вигляд:

(51)

Верхня половина правоїгілки гіперболи відповідає значенням параметра 0 t, нижня – значенням<t< 0.

Зауваження 2. Оптична властивістьгіперболи: промінь світла, що виходить із джерела світла, розміщеного в одному з фокусів гіперболи, після відбитка від гілки гіперболи рухається так, начебто він виходить з іншого фокуса.

Зауваження 3. Якщоа=b, то гіпербола називаєтьсярівнобічною. Її рівняння в канонічному вигляді

x²y²=a². (52)

Рис. 30. Рівнобічна гіпербола

Асимптоти y=xє бісектрисами координатних кутів.

Повернемо систему координат xOy на кут  = /4 (рис. 30) і запишемо рівняння гіперболи в системі координат хОу. Використовуючи формули перетворення координат при повороті осей (4), отримаємо:

(53)

Підставимо (53) у рівняння гіперболи (52):

(х + у)²(yx)²=2a², 4ху=2a,ху=k,у=k/x,k=a²/2.

У системі координат хОурівнобічна гіпербола описується рівнянням

у= (54)

Приклад 12.Звести до канонічного вигляду рівняння гіперболи

9x²16y²+ 64y54x– 127 = 0.

Розв’язання. Виділимо в рівнянні гіперболи повні квадрати. Маємо

9(x²6x+ 9)8116(y²4y+ 4) + 64127 = 0, 9(x 3)²16(y 2)²= 144,

де

Канонічне рівняння гіперболи отримане. Центр гіперболи точкаО’(3, 2). Півосі гіперболиa = 4, b = 3. Канонічна система координатОху(креслення зробіть самостійно).

4.6. Парабола

Канонічне рівняння параболи в декартовій формі:

. (55)

Точка F(p/2; 0)фокус параболи,x=p/2рівняння директриси

Рис. 31. Парабола

Основна властивість параболи: відстань від будь-якої точки параболи до фокуса дорівнює відстані від цієї точки до директриси. Доведемо цю властивість.

Зауваження 1. Оптична властивість параболи: усі промені, що виходять із фокуса параболи, після відбитка від параболи направлені паралельно її осі. Ця властивість параболи використовується в прожекторах, ліхтарях, локаторах.

Зауваження 2. Рівнянняy²=2px,x²= 2py,x²=2py(p> 0) також визначають параболи (рис. 32).

Рис. 32. Параболи (p > 0)

Приклад 13.Звести до канонічного вигляду рівняння параболи

x²4x8y+ 12 = 0.

Розв’язання. Запишемо рівняння параболи у вигляді:

(x²4x+4)8(y1) = 0; (x2)²= 8(y1),х²=8у,

де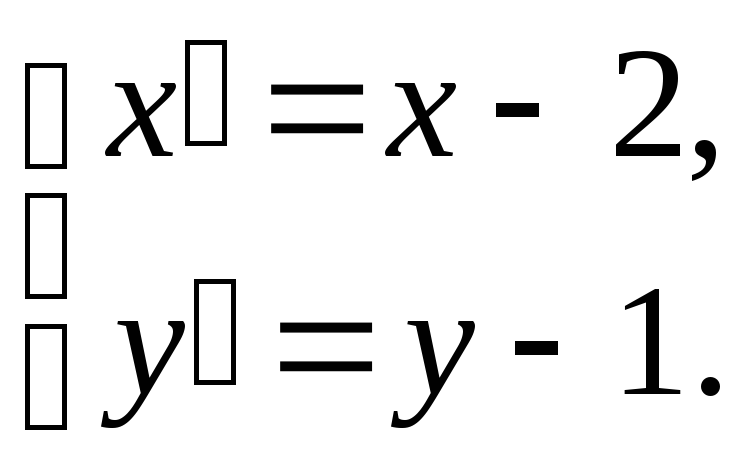

Вершина параболи точкаО(2, 1). Канонічна система координатхОу. Параметрр= 4 (креслення зробіть самостійно).