21(22) Диференциальные Уравнения движения твердого тела(поступательного, вращательного и плоскопараллельного движения твердого тела).

1 . поступательное

;

; ;

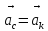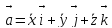
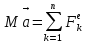
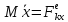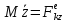
это диф. Уравнения поступательного движения в дек.координатах.

2. вращ. Движение

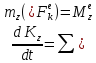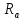в правой части нет и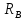, так как они пересекают ось вращения.

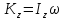
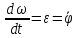
- диф. Уравнение вращ. Движения

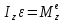- вращающий момент, 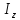- мера инертности тела при вращательном движении

3. плоско параллельное

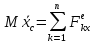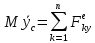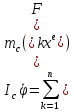; ;–диф. Уравнения плоско параллельного движения.

22(23). Кинетическая энергия материальной точки и механической системы. Определение кинетической энергии вращающегося тела. Теорема кенига.

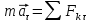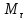–основной закон динамики спроецированный на касательную к траектории точкиM; ;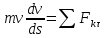– домножим наds и внесем m под дифференциал : 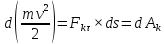; 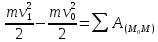- теорема об изменении кинетической енергии точки.

Кинетической энергией системы называется скалярная величина Т, равная сумме кинетических энергий всех точек системы. .

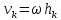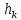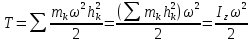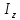Если тело вращается вокруг оси OZ то скорость любой точки , где- расстояние до оси. Тогда, где – момент инерции относительно оси вращения.

Теорема Кенига: кинетич. энергия мех. сист. = сумме кинетич. энергии центра масс системы, масса которого равна массе всей системы, и кинетич. энергии этой системы в ее относительном движении относительно центра масс.

(24). Определение кинетической энергии твердого тела при поступательном, вращательном и плоскопараллельном движениях.

Поступательное: все точки тела движутся с , тогда

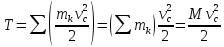
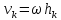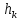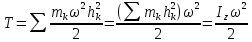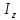Вращательное: Если тело вращается вокруг оси OZ то скорость любой точки , где- расстояние до оси. Тогда, где – момент инерции относительно оси вращения.

Плоско –параллельное: скорости всех точек распределены так, как если бы тело вращалось вокруг оси, перпендикулярной плоскости движения и проходящей через МЦС – Р. Тогда 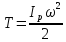,- переменная, так какP изменяется. Введем постоянную 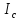относительно оси, проходящей через центр масс С. По т. Гюйгенса, гдеd=PC. Подставим, учитывая, что

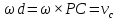
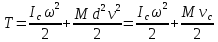
(25).Элементарная работа силы. Работа силы на конечном перемещении точки ее приложения. Мощность.

Элементраня работа силы F, приложенной в точке M это скалярная величина 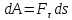, где - проекция силы на касательную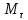к траектория точки М. так как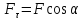, где- угол междуF и 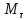, то. Работа силы на любом конечном перемещении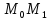, вычисляется как предел интегральной суммы соответствующих элементарных работ.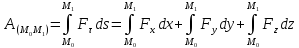

Мощность – работа в единицу времени, в общем случае .

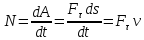26-27 Частные случаи вычисления работы сил.

1 работа силы тяжести: пусть точка М на которую действует сила тяжести Р перемещается из 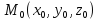в, тогда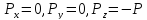, подставим в формулу работы:

2 работа 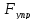:пусть 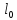- длина ненапряженной пружины, если оттянуть пружину грузом до велечины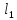, то удлинение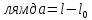и на груз действует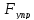. Работа, совершаемаяпри перемещинии груза из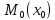в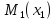состоит из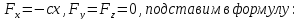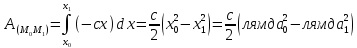3 работа 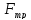:на точку движущуюся по поверхности действует 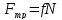. Она направелна противоположно движению 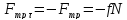и подставляя получим:.

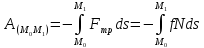(28). определение работы пары сил, приложенной к вращающемуся телу. Мощность.

Элементарная работа приложенной к телу силы F равна 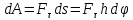, где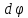- элементарный угол поворота, и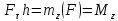- момент пары сил. Тогда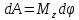, а при повороте на конечный угол , а при повороте на конечный угол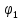работа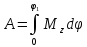, а при постоянном моменте.

Мощность – работа в единицу времени, в общем случае .

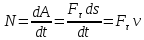29. 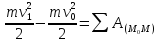- теорема об изменении кинетической енергии точки.

(30). Теорема об изменении кинетической энергии механической системы в дифференциальй и конечной форме. Теорема об изменении кинетической энергии точки.

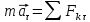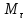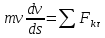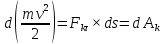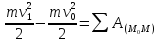–основной закон динамики спроецированный на касательную к траектории точкиM; ;– домножим наds и внесем m под дифференциал : -в дифференцмальной форме - теорема об изменении кинетической енергии точки в конечной форме.

Рассмотрим точку системы массой 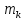и со скоростью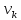, для этой точки. Составляя такие уравнения для каждой точки системы и складывая их почленно, найдем - в дифференциальной форме. Проинтегрируя при перемещении системы из положения где энергия равна в положение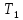получим 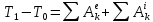– в конечном (интегральном виде).

31-32 Работа силы в потенциальном силовом поле. Потенциальная энергия.

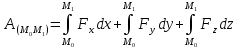. силовое поле задается уравнениями 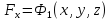,,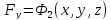. Для вычисления работы таких сил надо знать зависимости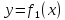,определяющие уравнение траектории точки М. однако если вывыражение под знаком интеграла будет полным дифференциалом функциито есть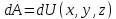или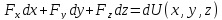то работу можно вычислить не зная траектории. ФункцияU называется силовой функцией, силовое поле для которого существует силовая функция называется потенциальным. Тогда работа сил .потенциальной энергией мат. Точки в полжении М называется скалярная величина П равная работе сил поля по перемещению точки из М в 0. 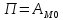или