TEP / lekcher_1

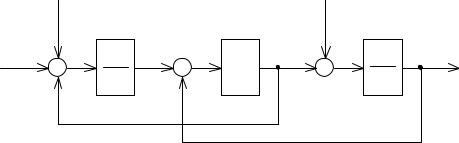
Составим структурную схему механической части согласно (13) и (14) :

M c1

M c 2

M c3

M (-)

1 ω1

C

M12 (-)

1 ω2

C

23

M 23

(-)

1 ω3

J1p

12

J2p

J3p

(-)

(-)

ω

p

(-)

(-)

ω

p

M12

2

M 23

3

В данной системе появятся автоколебания, т.к. есть перекрестные связи. ( ω1 - скорость двигателя).

Уравнения движения двухмассовой диссипативной системы ЭП.

β12

β12 учитывает внутреннее вязкое трение.

J1

J2

Согласно (10) запишем :

Mвнj

− Mпj − Mдj

= Mинj, j =1,2;

ω1

ω

момент

(16)

C12

2

диссипации

M

Mвн1

= M − Mc1

Mc1

M c 2

Mвн2

= −Mc2

(17)

Диссипативные моменты, т.е. обусловленные внутренним вязким трением элементов, определяются дифференцируя по функции Релея.

n−1	(ωj −ωj+1 )		2
Wд = ∑βвт j, j+1		2		(18)
j=1
Mдj = −βj−1, j (ωj−1		− ωj )+βj, j+1 (ωj −ωj+1 )		(19)
Mд1 =β12 (ω1 −ω2 )				(20)

Инерционные и потенциальные моменты определяются при J = const из (6) и

(8).

Mин1			= J1	dω1
				dt
				dω2
Mин2			= J2
					dt
M	п1	= C		∫	(ω −ω )dt
			12			1	2

Уравнения движения двухмассовой диссипативной системы :

					′		= J1	dω1
M − Mc1 − M12
′							dω2	dt
	− Mc2		= J2
M12							dt
′	= C12 ∫(ω1 − ω2 )dt +β12 (ω1 −ω2 )
M12
Преобразуем по Лапласу :
M(p)− M			c1	(p)− M′ (p)					= J pω	(p)
								12	1 1
′	(p)− Mc2 (p)= J2pω2 (p)
M12
		C12
′	(p)=					(ω1 −ω2 )+β12 (ω1 −ω2 )
M12
			p

(21)

(22)

(23)

(24)

(25)

Из (24) с учетом (25) составляем структурную схему двухмассовой диссипативной системы :

Mc1

M c 2

	(-)	1	ω	C		′	(-)	1	ω
M					+β	M12				2
			1	12
	(-)	J1p	(-)	p	12			J2p
		′		ω
		M12		2

Учет характера статических моментов при составлении структурных схем.

Рассмотрим 2-х массовую диссипативную систему (покажем как надо учитывать вид нагрузки).

1.Нагрузка – момент статический ( Mc ), приведенный к расчетной скорости;

2.Mc может быть потенциальным, активным или реактивным;

3.Mc зависит от вида механической характеристики рабочей машины

( Mc является функцией скорости при вентиляторной нагрузке). Реально в приводе имеют место всегда реактивные и в ряде случаев потенциальные нагрузки.

	′		= J1	dω1
M − Mc1 − M12				dt
			dω2
′	− Mc2 = J2
M12			dt
	= C12 ∫(ω1
′		− ω2 )dt +β12 (ω1 −ω2 )
M12

Пусть Mc создается реактивными и потенциальными нагрузками. Mc1 - эквивалент всех моментов приведенных к валу двигателя.

Mc1 = Mc1_ потенц +							Mc1_ реакт
						обусловленосухим
						трением
Mc2 = Mc2 _ потенц + Mc2 _ реакт + Mc2 _ вязк.трение
Mc1_ реакт =		Mc _ р1			sign (ω1 )			Знак	момента
								определяется	знаком
							sign (ω2 )
Mc2 _ реакт =			Mc _ р2					скорости.

После преобразований по Лапласу получаем структурную схему :

β12

(+)

Mc1

M c 2

(+)

(+)

Mc

ω

M

(-)

1 ω1

C12 +β

′

(-)

1

ω

M12

2

(-)

J1p

(-)

p

12

J2p

ω

′

2

M12

Mc1_ реакт

Mc

ω

В большинстве случаев к первой массе приложена только потенциальная

нагрузка. Ко второй массе – разные нагрузки (потенциальные, вязкое трение,

сухое трение и т.д.).

Учет зазора в передачах.

Рассмотрим на примере 2-х массовой диссипативной системы.

′

dω1

M − Mc1 − M12 = J1

dt

(27)

dω2

′

− Mc2 = J2

M12

dt

С12

Δϕз

ϕз - приведено к расчетной скорости

J1

J2

ω2 .

Mc1

M

Mc2

ω1

β12

ω2

n

m

Δϕз

= ∑Δϕз_ j ij + ∑( Si ρ )

(26)

j=1

i=1

i

Где

Δϕз_ j

−

Зазор каждого элемента;

ij

−

Передаточное отношение;

Si

−

Линейные элементы и их зазор.

В период выбора зазора механическая связь между массами J1 и J2 отсутствует (разрыв по силовому каналу), следовательно, уравнение движения (27) надо скорректировать.

Если

ϕ −ϕ

f

Δϕ

з

1

2

2

′

Δϕз

=β12 (ω1

−ω2 )+ C12

ϕ1 −ϕ2

±

M12

2

(28)

p Δϕз

Если

ϕ −ϕ

2

1

2

′

= 0

M12

Структурная схема в соответствии выражениям (27), (28) :

	Mc1
M (-)	1 ω1		1 ϕ1 − ϕ2			−	Δϕ	з
							2
(-)	J1p	(-)	p	(-)				+	Δϕз
	M′		ω2		Δϕкп				2
	12
								M c 2
					′		(-)		1	ω2
				C12 + β12 p	M12
									J2p

Δϕкп - погрешность в кинематической передаче.

Δϕкп = Δϕmax sin (Ωt)

Зазор в механической части – плохо, надо убирать. Для безударного пуска применяют ступени безударного пуска.

Механическая часть ЭП как объект управления. Исследование динамических свойств частотным методом.

Мы получили уравнения движения для одно, и много массовых систем, включая диссипативные и консервативные системы. Составили структурные схемы, которые позволяют анализировать динамические свойства системы.

При этом задающим воздействием является электромагнитный момент. Выходной, или регулируемой координатой является скорость 1-ой или 2-ой масс, путь, проходимый этими массами, ускорение и упругий момент 2-х

массовой системы. Возмущением являются моменты нагрузки Mc .

Одномассовая расчетная схема ( J = const ).

M − Mc

= J dω

M

Mи

1

ω

(-)

Jp

dt

Mc

Запишем передаточную функцию W(p) по входному воздействию :

Wω (p)=

ω(p)

=

1

(1)

M(p)

Jp

Запишем АФЧХ для этого звена :

π

1

1

1

Wω (p)

= Wω

(jω)=

= −j

=

e− j2

p=jω

jωJ

Jω

Jω

Wω (p)

= Wω

(jΩ)= −j

1

(2)

p=jΩ

JΩ

Wω (jΩ)= K(jΩ)

K – комплексный коэффициент передачи

K = A(Ω) ejϕ(Ω)

звена (системы).

a + jb =

a

2

+ b

2

e

j arctg(b a )

1+ j(ΩT)= 1+(ΩT)

2

e

j arctg(ΩT)

1

1

=

e− j arctg(ΩT)

1+ jΩT

1+

(ΩT)2

Wω (jΩ)=

1

e−j

π

2

Jω

Aω (Ω)

=

1

ϕ(Ω)

= − π = const

(3)

JΩ

2

	ЛАХ системы :	1
	L(ω)= 20lg				= 20lg(1)− 20lg(JΩ)=
		JΩ

= −20lg(JΩ)= 20lg	1		+ 20lg		1		=
	J				Ω

=20lg 1 − 20lg(Ω)

J

Ω- частота, условно подавляемая на входе системы. В ТАУ исследуют поведение системы при воздействии :

1.Ступенчатого сигнала, результат – частотная функция h(t);

2.Функции Дирака, результат – весовая функция.

Aω (Ω)
	АЧХ
		L		ЛАХ
		−20	дб
		1	дек
				ω		=	1
	20lg
		J			ср		J
		0.1	1	10			lg(ω)
	Ω
−	π
	2
ϕ(Ω)

Рис.1б	Рис.1в
Механическая часть при пренебрежении	упругими связями

представляет собой интегрирующее звено (интегратор), или фильтр низких частот (ПИ-регулятор – избирательный фильтр).

1.При Ω →0, то скорость (выходная координата) стремится к бесконечности (это свойство интегратора, т.е. если M = Mc (входное

dω	= 0
воздействие равно 0), то dt	, следовательно, имеет место

установившийся режим, т.е. заданная скорость при заданной нагрузке

ωc ).

2.При колебании входного воздействия (т.е. либо колебания момента

электромагнитного, либо колебания момента статического) с некоторой циклической частотой ω, амплитуда колебания скорости

ограничена моментом инерции, причем тем в большей степени, чем выше частота (это и есть проявление фильтра НЧ).

3.Если момент избыточный постоянен, следовательно скорость должна изменяться по линейному закону.

Двухмассовая консервативная система.
	M c1					Mc2
M (-)	1 ω1			C	M12 (-)	1	ω2
	J1p			12		J2p
(-)		(-)	ω	p	(-)
	M12			2
				Рис.2
Возмущающим воздействием являются Mc1 и Mc2 . Управляемые
координаты M12 , ω1 , ω2 . Проанализируем динамические свойства данной
системы для 2-х случаев :

1.При отработке задающего воздействия, принимая Mc1 = Mc2 = 0.

2.При отработке возмущающего воздействия (основная нагрузка чаще

всего приложена ко 2-ой массе), следовательно Mc2 - возмущающее воздействие, а M = Mc1 = 0.

ВТАУ исследовать систему по возмущению и по заданию можно отдельно при линейной системе. Далее можно применить к ней метод суперпозиции, т.е. решение дифференциальных уравнений есть сумма решений свободной и вынужденной составляющих. Если система не линейна, то такое разделение не даст нам исследование динамики, надо прибегать к описанию системы методом переменных состояния.

В нашем случае система линейна, т.к. принимаем допущения J = const, C12 = const . Исследуем систему по заданию и по возмущению отдельно. Запишем передаточную функцию механической части ЭП по задающему воздействию, считая выходной координатой скорость рабочего

	органа ω2 .	ω	(p)			Ω2
	Wω2 (p)=			= p(J1			+ Ω122 )	(4)
		M	(p)			+ J2 )(p2
		2				12

ωсреза

Ω =

C12 (J1 + J2 )

12

J1J2

− частота свободных

колебаний системы

(собственная частота).

Обозначим :

1

T =

J

= J

+ J

Ω

Σ

1

2

0

, подставляя в (4) получаем (5) :

12

Wω2 (p)=

1

(5)

JΣp(T02p2 +1)

Система содержит консервативное

M

1

1

ω2

(идеальное

колебательное) звено,

J

p

T2p2

+1

Σ

включенное

последовательно с

0

Рис.3

интегрирующим звеном.

Очевидно, что свободное движение системы будет определяться видом
корней характеристического уравнения.
JΣp(T02p2 +1)= 0
p	= ±j	1
		T		p		= 0	p1,2 = ±jΩ12
1,2					3
	0

Т.е. при отсутствии в системе диссипативных сил (или любых сил, зависящих от скорости) двухмассовая консервативная механическая система представляет собой идеальное колебательное звено, т.е. звеном без

затуханий, причем Ω12 является частотой свободных колебаний этой системы. Проанализируем частоту свободных колебаний :

1. Ω12 прямо пропорциональна C12 . Среднечастотная часть определяет динамику системы, причем среднечастотная часть находится в области

ωсреза. Частота среза определяет быстродействие системы (способность системы отрабатывать задающее воздействие за заданное время). Чем

больше системы, тем меньше время регулирования. Есть высокочастотная часть, которая находится правее первой частоты сопряжения, находится за частотой среза. Эти частоты отфильтровываются системой (не влияют на динамику работы привода). Колебания в системе нежелательны, для их подавления

необходимо увеличить C12 . Если C12 очень большая величина, то пренебрегаем упругими свойствами системы, т.к. колебания будут подавлены самой системой. Можно перейти к простой одномассовой расчетной схеме.

2.Частота свободных колебаний обратно пропорциональна J1 и J2 . В регулируемом ЭП чаще всего и легче всего контролировать скорость

ω1. Оценим изменение скорости ω1 по задающему воздействию.

W(p)=

ω

(p)

1

Mc1 = Mc2 = 0

M

(p)

p

2

+

J

Ω

2

(p)

1

ω1

12

Wω

(p)=

=

JΣ

(7)

M

(p)

J1p(p2 +Ω122 )

1

Обозначим (очень часто J1 соизмеримо со всеми приводимыми моментами инерции системы) :

γ =

JΣ

J

, получаем :

1

Wω1 (p)=

γT2p2

+1

0

(8)

JΣp(T02p2 +1)

M

1

γT2p2

+1

1

ω1

J

p

T2p2

+1

0

Σ

0

Рис.4 В отличие от (5) появилось форсирующее звено в числителе. Если полюса и

нули характеристического уравнения совпадают, то они компенсируют друг друга. Механическая часть как объект управления при входном воздействии

M , при выходной координате ω1 можно представить в виде 3-х последовательно включенных звеньев (интегрирующее, форсирующее, колебательное).

M

1

γT02p2 +1

ω1

1

ω2

J

p

T

2p2

+1

γT2p2

+1

Σ

0

0

Рис.5

Передаточная функция, устанавливающая связь между ω1 и ω2 :

W

(p)=

ω2

(p)

=

1

(9)

ω

(p)

γT2p2 +1

ω1 ,ω2

1

0

Проанализируем динамические свойства исследуемой системы частотным методом. АФЧХ для рис.4 по задающему воздействию :