TEP / lekcher_1

W	(jΩ)=	1− γT2Ω2	= A		(Ω)e	−jϕω (Ω)
		0				1	(10)
		(jJΣΩ)(1+ T02Ω2 )
ω1				ω1

Используем метод асимптотических ЛАЧХ. Представим систему, описанную выражением (8), в виде рис.4, т.е. последовательно включены интегрирующее и форсирующее 2-го порядка звенья с частотой сопряжения :

Ωc1 = Ω12γ

иидеального колебательного звена с частотой автоколебаний (вторая частота

сопряжения) :

Ωc2 = Ω12

Устремляем частоты исследуемых колебаний в 0, в ∞ и к частотам сопряжения.

1. При Ω → 0 выражение (10) вырождается в АФЧХ интегрирующего

	звана		( JΣ = J1 + J2 ).		Низкочастотная асимптота имеет наклон
	−20		Дб			1
		Дек		, а коэффициент передачи		JΣ	.

2.При Ω →∞ выражение (10) вырождается в АФЧХ интегрирующего звена, но коэффициент передачи больше в γ раз. В низкочастотной и в

высокочастотной части наклон −20							Дб			π
								, сдвинут по фазе на −
							Дек			2 .
				Ω	c1	= Ω12
						γ ЛАХ	стремится к −∞,
3. При	частоте								имеем нуль
передаточной функции (8), который находится из (11).
γ 2	2 +	1	=	0						(11)
T0 p

При этом скачком изменяется знак числителя (10) на противоположный. Что соответствует уменьшению фазового сдвига на

π. ЛАХ асимптотична и в −∞.

4.При частоте сопряжения Ωc2 = Ω12 имеется полюс. Передаточная функция (8) имеет разрыв, ЛАХ стремится к +∞. При этом скачком

изменяется знак знаменателя (10), что соответствует увеличению фазового сдвига на π. Амплитуда колебаний стремится к ∞, при данной частоте резонанс.

	Lω
	1
			частоты
			сопряжения
				Lω1
					L ω1
	Дб	20lg (γ)
	−20 Дек
20lg	1
	JΣ
	Lω1	1	Ω12	Ω12			Ω
			γ
	−π
	2				ϕω
					1
	ϕω	резонанс		резонанс
	1
				Рис.6			= Ω12
					Ω	c1
							γ
В реальном приводе нас интересует резонанс при								(близок к
ωсреза), т.к. это опасно для механической системы.
Исследуем частотные характеристики по задающему воздействию,
когда выходная координата ω2 . Подставим в (5)					p = jΩ, получим уравнение
АФЧХ :		1
Wω2 (p)= jJΣΩ(1− T02Ω2 )								(12)
Проанализируем (12) :

1.В низкочастотной части, т.е. когда Ω → 0 ЛАЧХ по ω2 ( Lω2 )

совпадает с Lω1 , т.е. имеет наклон −20 ДекДб . Если частота колебаний нулевая, то вторая масса в точности повторяет колебания первой.

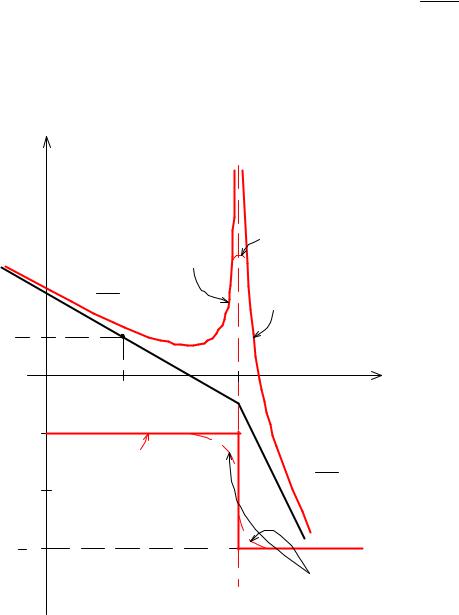
2.При частоте сопряжения Ω = Ω12 имеет место разрыв ЛАХ, т.е. ЛАХ стремится к +∞, а фазовый сдвиг увеличивается на π.

−60 Дб

3. При

Ω →∞

ЛАХ

стремится

к

асимптоте

Дек.

Если

задемпфировать колебания (вязкое трение, например), то резонанс

будет, но он реальный, т.е. происходит не бесконечное увеличение

амплитуды, а ограниченное. Энергия колебаний будет подавляться в

виде тепловой энергии в упругом элементе.

Lω

2

если в системе

Lω2

есть демпфирование

−20

Дб

Lω2

Дек

1

20lg

JΣ

1

Ω12

Ω

−

π

2

ϕω

Дб

2

−60

−π

Дек

−3

π

резонанс

2

если в системе

ϕω

есть демпфирование

2

Рис.7

Рассмотрим механическую часть как объект управления при входном

возмущающем воздействии

Mc2

(система линейная, следовательно можно

исследовать

отдельно

каждое

воздействие

исходя

из

принципа

суперпозиции).

M = 0, Mc

= 0

, имеется одно воздействие

Mc

2 ,

выходная

1

координата скорость ω2 . В соответствии с рисунком 2 передаточная

функция :

Wω′

(p)=

ω2 (p)

=

γ

T2p2 +1

2

0

2

Mc2

(p)

JΣp(T02p2 +1)

γ

2

=

JΣ

=

J1

γ

J2

J2

J

2

2

1

γT

p

+1

J2

0

Wω′

(p)=

(13)

2

JΣp

(T02p2 +1)

Аналогично из рисунка 2 можно записать передаточную функцию по

скорости ω1 при воздействии нагрузки Mc2 .

Wω′1 (p)=

ω1 (p)

=

1

= Wω2

(p)

(14)

Mc2 (p)

JΣp(T02p2 +1)

Если сравнить (13) и (8), то они подобны, аналогично видна идентичность (14) и (5). Это позволяет исследовать частотные свойства 2-х массовой консервативной системы по аналогии с ранее рассмотренными (по аналогии с (8)).

Врезультате выводы :

1.В низкочастотной области динамические свойства механической части

	−20	Дб
		Дек,
	определяются интегрирующим звеном (наклон

Kт = 20lg J1Σ ). Значит движение первой массы определяется при небольших частотах колебаний как управляющее воздействие, т.е. воздействие электромагнитного момента, возмущающего момента

Mc2 , суммарный момент инерции при этом JΣ = J1 + J2 . Другими словами, интегрирующее звено (рисунок 3, 4, 5) характеризует условие движение механической части в среднем, на которое накладываются колебания, обусловленные упругой связью (мы можем задать любой график движения, но на это движение будут накладываться высокочастотные колебания).

2.При приближении частоты колебаний электромагнитного момента M

или нагрузки Mc2 к резонансной частоте Ω12 (частота свободных колебаний) амплитуда колебаний скорости машины ω1 возрастает

Ωср жел

1

JΣp ),

схему.

(вплоть до бесконечности при ω = Ω12 , теоретически это так, но на практике нет).

Можно выявить условия, при которых влияние упругости будет незначительным, следовательно, можно перейти от 2-х массовой системы к одномассовой. Если одно из условий не выполняется, то такое преобразование делать нельзя.

а) Когда J1 J2 , следовательно γ →1 (основная масса – машина, вторая масса ничтожно мала, соединена с первой через упругую связь). Движение второй массы полностью определяется первой массой

1

(определяется интегрирующим звеном JΣp ), следовательно, можно применять одномассовую расчетную схему.

б) Когда C12 → ∞ (абсолютно жесткая связь) или J2 → 0, то Ω12 → ∞, следовательно, в области малых и средних частот движение первой массы является определяющим (определяется интегрирующим звеном

следовательно можно применять одномассовую расчетную

- частота среза ЛАХ разомкнутого контура регулирования (имеется ввиду скорректированная система). Обычно достаточно обеспечить это различие на порядок :

Ω12 f10Ωср жел

(15)

Если оценивать желаемое время регулирования (один из показателей качества), то из (15) следует выражение (пренебрегая упругими связями при расчете регуляторов системы) :

	tрег жел ≥ 40π		J1J2	(16)
		C12	(J1 + J2 )

Здесь учтено свойство линейной системы (желаемой) у которой наклон

	−20	Дб
		Дек.
	желаемой ЛАХ в области частоты среза имеет

Ωср жел = t 4π рег жел

3. В высокочастотной части ЛАХ Lω1 и Lω2 различны (наклон Lω2

−60 Дб

Дек, следовательно, колебательность массы 2 больше). Следовательно, при любых соотношениях параметров механической

части (т.е. при любых γ), в случае, когда частота задающего

воздействия больше собственной частоты колебаний ( Ω f Ω12 ) есть существенные резонансные колебания. В таких случаях при построении ЭП с требуемым качеством регулирования движения 2-ой массы, или при введении обратных связей по координатам 2-ой массы учет упругих свойств всегда обязателен (иначе система войдет в режим автоколебаний и станет неработоспособна).

4.Реально амплитуды резонансных колебаний несильно демпфируются диссипативными силами, присутствующими в реальной механической части ЭП (если есть внутреннее вязкое трение, следовательно имеется конечное значение амплитуды в области резонанса). Важна оценка, насколько реальное механическое вязкое трение в системе (силы диссипации) способны задемпфировать колебания (если полностью демпфируются, то при синтезе систем не будут учитываться эти резонансные явления; если это не так, то мы обязаны средствами ЭП подавлять эти колебания).

Исследуем структурную схему двухмассовой диссипативной

механической системы ЭП.

′

= C12

Δϕ + δ12

Δω

M12

Mc1

M c 2

(-)

1

ω

C

′

(-)

1

ω

M

M12

2

1

12 +β

(-)

J1p

(-)

p

12

J2p

′

ω

M12

2

Рис.8

Передаточная функция системы по возмущающему воздействию Mc2 , при

выходной координате ω1 :

+ C12

ω1

(p)

β

p

Wω′

(p)=

=

12

(17)

J J

p2

+(J

+ J

p

+ C

)

1

M

c2

(p)

2

)(β

1

2

1

12

12

				Ω12 =			C12JΣ		T =	1
							J J			Ω
Обозначим :									0
					1 2 ,					12
Коэффициент затухания (ослабления внутреннего вязкого трения) :
α	вт	=	β12 (J1 + J2 )
			2J1J2
После подстановки в (17) получаем :
Wω′1 (p)=					2αвтT0p +1					(18)
				JΣp(T02p2 + 2αвтT0p +1)

Оценим динамику, воспользовавшись характеристическим уравнением :

p	= −α	вт	± j	Ω2 −α2
1,2				12	вт
				14243
				Ωр −реальная собственная		p3 = 0
				частота системы	,

Сравнивая (19) и (6) видно, что учет внутреннего вязкого трения вводит в

систему демпфирование (собственная частота колебаний уменьшилась и 2-х массовая диссипативная механическая система приобретает свойства

реального колебательного звена с коэффициентом затухания αвт и частотой

Ω2	− α2
колебаний 12	вт ).

Оценим демпфирование. Исследование реальных систем для большинства случаев показывает, что внутренние силы вязкого трения малы (Если большой коэффициент внутреннего вязкого трения то при колебаниях

всистеме имеются потери энергии. Надо сообщать дополнительную энергию, но тогда передача обладает низким КПД. Механики стремятся устранять внутреннее вязкое трение). На практике есть специальные системы, например, пластично-деформирующие (ременная передача). Они вызывают естественное затухание колебаний под действием внутренних сил вязкого трения, но ничтожно малого. Логарифмический декремент затухания

вэтой системе :

λвт =	2πα вт =	2παвт			(20)
	Ωр	Ω2	−α2
		12	вт
Пределы этого значения в реальных системах :					0.1 ≤ λвт ≤ 0.3. Учет

естественного демпфирования существенно не сказывается на форме ЛАЧХ и ФЧХ, но ограничивает разностный пик некоторым конечным значением

(уже хорошо, система не развалится). Т.к. αвт	Ω12 , то реальная частота
близка частоте собственных колебаний.

Для определения коэффициента резонансного усиления можно исследовать АФЧХ нашей системы (для этого в (18) необходимо произвести

подстановку	p → jω	,	ω = Ω		,	Ω12	Ωреальн.				). В результате коэффициент
				12
резонансного усиления :
Kрезонансного усиления				π2	+ λ2			π
						вт					(21)
								λ
					λ2				вт
						вт

Очевидно, из (21) в зоне резонанса вынужденные колебания устанавливаются в (10 ÷ 30) раз больше. Однако, если сравнивать с механикой консервативной системы (где в момент резонанса имеют место бесконечные амплитуды, здесь свойства механической части существенно изменились). Необходимость учета естественного демпфирования обязательна, когда исследуются вынужденные колебания, а другие демпфирующие факторы в системе отсутствуют.

При математическом моделировании переходных процессов также следует учитывать демпфирование, т.к. в противном случае возникающие колебания затрудняют правильное представление о их характере.

При решении конкретных задач коэффициент внутреннего вязкого трения, как правило, не задается (но есть формула, которая позволяет его

определить из условия 0.1 ≤ λвт ≤ 0.3). Эмпирическая формула :

β12	(0.1÷0.3)	C12	J1J2		(22)
	π		J + J	2
		1

Если применяются люфты, то внутреннее вязкое трение больше, т.к. в люфах резина.

В настоящее время самое слабое звено в ЭП с точки зрения динамики – это электрическая машина. Самая лучшая машина – асинхронный двигатель с К.З. ротором (с точки зрения динамики).

Механические переходные процессы в одномассовой системе ЭП.

С точки зрения решения задачи – легко, т.к. требуется решить дифференциальное уравнение 1-го порядка. Переходный процесс – переход из одного установившегося состояния в другое, даже если второе состояние может быть и не достигнуто, тогда привод всегда работает в динамике (в квазистационарном режиме). Переходный процесс обусловлен тем, что имеет место инерционность.

Рассмотрим динамику, оценивая только механическую инерцию (для простоты рассуждений). J = const

Уравнение движения одномассовой системы :
M − Mc		= J dω					(1)
		dt
Оценим движение системы по суммарному воздействию M и Mc .
1. Mc = const ,			следовательно	Mизбыт	= const ,		движение
равноускоренное.						Mc , Mизбыт f 0
M,ω				Пусть задан
				во	время	переходного
M1			ω(t)	процесса. Конечное			значение
				скорости		определяется
ω				равенством		Mэм = Mc		,
кон			M (t )
				начальное значение			скорости
Mc				равно 0.
0		tп.п.	t
Найдем зависимость ω(t) (решим 1) :
M − Mc		dt = dω	M − Mc	=ε dω= εdt
J			J
Проинтегрируем :
ωкон		t
∫ dω=		∫εdt
ωнач		0
ω(t)= ωнач + εt							(2)
Если заранее известно конечное значение скорости ( ωконечн), то можно
получить время переходного процесса :
tп.п. = ωкон −ωнач			ε = Mизбыт
Окончательно :		ε	J
tп.п. =	J(ωкон −ωнач )
		M1 − Mc
Эта формула позволяет определить закон управления ускорением. Если
задано ускорение, то можно найти Mизбыт ,				обеспечивающий это ускорение,
если считать, что разгон привода равноускоренный.

2.

Влияние вида нагрузки на характер переходного процесса.

1.

Реверс привода при реактивном моменте на валу. Примем допущения

Mc = const ,

т.е. это

крановый

момент,

но

реактивный

Mc = Mc sign(ω) знак момента изменяется.

M,ω

При t = 0− :

M = Mc

ωнач.

ω = ωнач .

t = 0+

Mc

Очевидно,

при

происходит

реверс,

ω(t)

момент

машины

изменяется

скачком

до

tп.п.

−M

Происходит

0

tт

t

1.

торможение

привода.

Если

−ωконечн.

M (t )

M1 = Mc = const ,

то

происходит

−M1

равнозамедленное

ω= ω − M1 + Mc t

движение.

нач

J

Машина создает тормозной момент, работает в режиме противовключения.

При торможении привода ω= 0. Момент времени торможения :

tт = J

ωнач

M1 + Mc

Далее, при

t f tт

скорость машины изменяет знак,

происходит разгон в

противоположную сторону. Момент статический изменяет знак в силу того,

что нагрузка реактивная и момент M = Mc

sign(ω),

разгон происходит с

меньшим ускорением. При этом :

ω= − M1 − Mc t

ε = M1 − Mc

J

J

Когда

Mэ = Mc,

то

момент

электромагнитный

изменяется

скачком,

устанавливается режим

Mэ = −Mc , ω = −ωконечн. .

Переходный

процесс

состоит из 2-х участков, причем при реактивной нагрузке ускорение пуска и

ускорение торможения различны.