Математичні моделі в економіці Ден. Маг. 2015 Чупилко

Для наочного уявлення взаємозамінюваності факторів можна побудувати ізокванту – геометричне місце точок факторів L, K , для яких показник обсягу виробництва продукції X залишається сталим. Щоб побудувати ізокванту, виразимо один із факторів виробничої регресії через інший фактор і стале значення показника регресії Y0:

K

( X 0 / A)1/

1 / L 2 /

1 .

(29)

Якщо сталу

( X 0 / A)1/ 1 позначити

через b, то отримаємо

таку

залежність:

K

b / L 2 / 1 .

Частинні похідні випуску за чинниками називають граничними

продуктами або граничними (маржинальними) ефективностями чинників.

Легко помітити, що SK SL

1.

Для мультиплікативної виробничої функції норма заміщення праці

фондами пропорційна фондоозброєності:

S

2 K

2

k ,

k

K

,

(30)

K

1L

L

1

що є логічним, адже брак обсягів праці можна компенсувати кращою фондоозброєністю.

За допомогою ВФ можна описати ефективність та масштаб виробництва. Перейдемо до відносних (безрозмірних) показників у ВФ:

Х

K

1

L

2

, де X0

, K0, L0 – значення обсягів випуску і витрат фондів та

Х 0

K0

L0

праці в базовому році.

Приведемо безрозмірну форму до початкового вигляду виробничої

функції:

X

X 0

K 1 L 2 .

(31)

K

0

1 L 2

0

Отже, коефіцієнт А зіставляє ресурси з випуском.

У відносних (безрозмірних) одиницях ВФ можна записати таким

~

~

~

(32)

X

K 1 L 2 ,

~

X

~

K

~

L

де

X

,

K

,

L

.

(33)

X 0

K0

L0

Ефективність – це відношення результату до витрат. У нашому випадку є

~

~

два часткових показника ефективності:

X

- фондовіддача;

X

- продуктивність

~

~

K

L

праці. Коефіцієнт ефективності можна записати у такій формі:

~

~

1

Е

X

X

,

(34)

~

~

K

L

роль вагових коефіцієнтів тут відіграють відносні еластичності за фондами і працею:

21

	1	,		1		2	,		(35)
1		2			1		2

тобто часткові ефективності входять до загальної ефективності з такими самими пріоритетами, з якими входять у ВФ відповідні ресурси.

За допомогою коефіцієнта економічної ефективності ВФ можна подати у

формі, яка зовнішньо збігається з функцією Кобба-Дугласа:
	~	~ ~1	(36)
	X	EK L .
Масштаб виробництва визначається як середнє геометричне темпів
зростання використаних ресурсів:		~ ~1
	M		(37)
		K L .
Отже, випуск є добутком економічної ефективності та масштабу
виробництва:	~
		EM .	(38)
	X
Математична теорія фірми, зокрема, оптимізаційні задачі в різних
сферах людської діяльності пов’язані		із поняттям похідної.	Розв’язування

таких задач засновано на дослідженні функцій методами диференціального числення.

Розглянемо задачу максимізації прибутку фірми, яка випускає продукцію одного виду. Розрізняють випадки досконалої ринкової конкуренції і монополії щодо ціни на продукцію. Докладно – в рекомендованій літературі [2].

Розглянемо випадок сталої ціни. Якщо підприємство виробило продукції

y одиниць (кг, тон і т.ін.), то при її реалізації за ціною	p дохід складе:
R( y) py .	(39)

Функція витрат визначається розподілом вихідних даних. Якщо розподіл витрат, наприклад, можна описати квадратичною функцією, то відповідна регресія має вигляд:

С( у)	а	0	а у	а	2	у2 .	(40)
			1
Це рівняння треба звести до	лінійного			заміною змінних			і визначити

параметри економетричними методами, використовуючи вихідні дані. (див. навчально-методичний посібник «Економіко-математичні методи та моделі. Частина 2», тема 3 [4]).

Прибуток визначиться таким чином:

F ( y)	py	a	0		a y a		2	y2 .	(41)
					1
Для визначення максимуму прибутку треба задовольнити необхідну
умову екстремуму функції однієї змінної:
F ( y)	p		a1		2a2 y			0 .	(42)
З цього рівняння отримаємо значення					у , за якого функція прибутку має
екстремум:
	у			p	a1	.			(43)
				2a2

22

З огляду на те, що функція прибутку квадратична, опукла вгору, то маємо максимум. У цьому можна переконатися, якщо знайти другу похідну функції прибутку, і, таким чином, задовольнити достатню умову існування екстремуму.

Щоб знайти максимальний прибуток, треба визначене значення у підставити у функцію прибутку.

В оптимальному розв’язку маржинальний дохід та маржинальні витрати мають однакові значення.

Питання для самоконтролю

1.В чому полягає граничний аналіз в економіці? Наведіть приклади для задач, пов’язаних з фінансовою діяльністю підприємства.

2.Наведіть основні виробничі функції, що використовуються для опису економічних процесів.

3.Мультиплікативна виробнича функція та її особливості.

4.Застосування методів диференціального числення для розв’язування задач фірми.

5.Бар’єрні показники у фінансовому аналізі.

Завдання до самостійної роботи

Завдання 1

Є дані про металургійний сектор в Україні:

	Обсяг продукції,	Витрати праці, млн.	Витрати капіталу,
Рік	млн. у.о.	днів	млн. у.о.
	У	Х1	Х2
1992	12767	375	131427
1993	16347	402	134267
1994	19542	478	139038
1995	21075	553	146450
1996	23052	616	153714
1997	26128	695	164783
1998	29563	790	176864
1999	33376	816	188146
2000	38354	848	205841
2001	46868	873	221748
2002	54308	999	239715

Побудувати функцію типа Кобба-Дугласа, яка описує залежність між випуском продукції металургійної галузі, затратами праці та витратами

капіталу:

Y=a0X1a1X2a2.

23

Розрахувати її параметри МНК, знайти коефіцієнт детермінації та оцінений коефіцієнт детермінації, стандартні квадратичні відхилення для параметрів регресії.

З надійністю Р=0.95 встановити адекватність прийнятої математичної моделі статистичним даним.

Якщо модель адекватна статистичним даним, то знайти частинні коефіцієнти еластичності, значення прогнозу і його надійний інтервал при Х1=1000, Х2=250000, дати економічну інтерпретацію результатам.

Побудувати ізокванту для випуску Y=55000млн. у.о. Оцінити масштаб і ефективність виробництва. Використовуючи розрахунки, зробити висновки.

Завдання 2

В таблиці наведені витрати С та кількість виробленої підприємством продукції У. Визначити, який максимальний прибуток отримає підприємство, якщо реалізуватиме цю продукцію за ціною Р=10 у.о.

Насамперед, побудувати функцію витрат, використовуючи економетричні методи та прийнявши квадратичний закон залежності між У та С.

У	25	37	40	42	48	62	53	47	69	63	73	49
С	195	215	235	245	287	375	334	285	450	420	690	450

Задачу розв’язати такими способами:

1.За допомогою методів диференціального числення.

2.Графічно, побудувавши графіки функцій витрат і прибутку.

Рекомендована література

[1, 3, 4]

Тема 3. Моделювання діяльності підприємства із застосуванням методів математичного програмування

План вивчення теми

1.Виробнича задача лінійного програмування: пряма та двоїста задачі. Виробнича програма підприємства.

2.Аналіз рентабельності продукції та дефіцитності ресурсів, коефіцієнтів цільової функції. Аналіз двоїстих оцінок.

3.Нелінійне програмування. Методи розв’язування задач нелінійного програмування. Оптимізаційні розв’язки.

4.Моделювання сфери попиту. Задача оптимізації споживчого вибору.

24

5.Моделювання сфери виробництва. Комбінація ресурсів, що максимізує об’єм випуску при обмеженнях на витрати. Комбінація ресурсів, що мінімізує витрати при фіксованому об’ємі випуску.

6.Моделі та задачі транспортного та розподільчого типів.

7.Використання процедури «Поиск решения» в EXCEL для оптимізаційного розв’язку економічних задач.

Навчальні цілі

Ознайомити студентів із застосовуванням методів математичного програмування та процедури «Поиск решения» в EXCEL для оптимізаційного розв’язку задач економіки та фінансів.

Завдання та методичні рекомендації до вивчення теми

Постановка задач лінійного програмування (пряма і двоїста), а також методи розв’язування докладно розглядалися в дисципліні «Економікоматематичні методи та моделі. Частина 1» [3]. Можна також звернутися до літератури, що вказана до даної теми.

До задач, що використовують оптимізаційні методи, можна віднести задачі складання оптимального плану виробництва продукції, оптимального складу портфеля цінних паперів, раціонального розподілу робітників на виробництві і т.ін.

Часто на практиці використовуються сполуки моделей, наприклад, економетричних для побудови залежності між показником та факторами, і далі оптимізаційних, для яких використовуються методи лінійного або нелінійного математичного програмування.

Для прикладу розглянемо спочатку задачу оптимізації споживчого вибору [1]. Споживач завжди прагне максимізувати свою корисність, але його стримує обмежений дохід, тобто задачею вибору споживача (задача раціональної поведінки споживача на ринку) є вибір такого споживацького набору, який максимізує його функцію корисності при заданому бюджетному обмеженні.

Формально, цю задачу можна записати у вигляді:

U (x1 , x2 ,...,xn ) max		(44)
при обмеженнях:
n
pi xi	M
i 1	,	(45)

xi 0

де М – доход, який споживач має намір повністю витратити на придбання споживацького набору для досягнення максимальної корисності, рі – ціна і-го блага.

25

Рис. 1 Геометричний розв’язок задачі споживача

Перше обмеження – бюджетне – встановлює максимальну вартість споживацького набору, друге обмеження витікає з умови, що такі економічні змінні, як кількість благ, не можуть бути від’ємними. У випадку двох благ бюджетне обмеження має вигляд трикутника. Оптимальний розв’язок співпадає з точкою дотику лінії обмеження і лінії байдужості.

Отже, треба знайти такий невід’ємний набор благ X * (x1* , x2* ,...,xn* ) , який принесе споживачу максимум корисності при існуючому бюджетному

обмеженні.

Математично, це є задача

на

умовний екстремум з обмеженнями, яку

можна звести до задачі на

безумовний екстремум функції Лагранжа, яка має

вигляд :

n

L(x1 , x2 ,...,xn ,

)

U (x1 , x2 ,...,xn )

pi xi

M .

(46)

i

1

Необхідні умови існування безумовного екстремуму:

L

0, i

1, n

xi

(47)

L

0.

U (x* , x* ,...,x* )

* p

1

2

n

, i

1, n

xi

i

звідки :

(48)

n

pi xi*

M

0.

i 1

Знайдений із цієї системи розв’язок X * (x* , x*

,...,x* )

і є розв’язком

задачі

1

2

n

раціональної поведінки споживача на ринку.

Із перших n рівнянь останньої системи витікає:

26

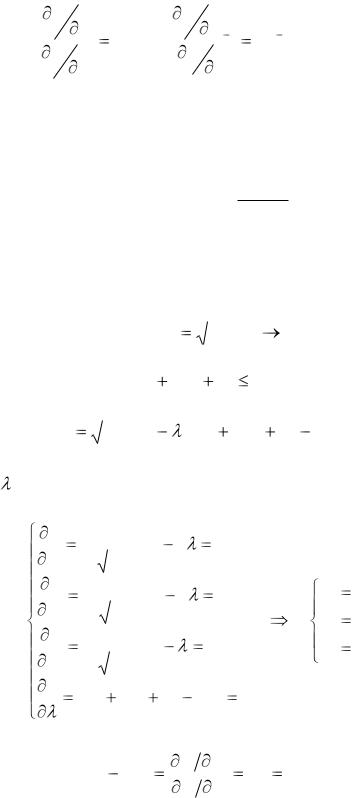
U x1

p1

, ...,

U

xn 1

pn 1

.

(49)

U

U

p2

xn

pn

x2

Тобто

споживач за

фіксованого

доходу обирає

такий набір

благ

X * (x* , x* ,...,x* ) , що в цій точці відношення граничних

корисностей

благ

1 2

n

дорівнює відношенню їх цін.

Приклад . Визначити, який набір товарів обере споживач, який має дохід у 300 гр.од., якщо його функція корисності має вигляд

U(x1 , x2 , x3 ) x1 x2 x3 ,

аціни товарів відповідно дорівнюють: р1 = 2 гр.од.; р2 = 4 гр.од.; р3 = 1 гр.од. за одну одиницю. Знайти граничну норму заміни другого товару першим.

Розв’язування.

Математична постановка задачі: Знайти кількість товарів x1 , x2 , x3 таку,

щоб	U (x1 , x2 , x3 )				x1 x2 x3			max
при бюджетному обмеженні:
		2x1		4x2	x3	300
Запишемо функцію Лагранжа
	L	x1x2 x3		(2x1		4x2		x3 300)
Розв’язування	вихідної	задачі		зводиться до				визначення такого набору

значень x1* , x2* , x3* , * , за якого функція Лагранжа буде мати максимум. Із необхідних умов екстремуму функції Лагранжа маємо:

L				1						x2 x3		2			0
x1		2
										x1 x2 x3
L		1								x1 x3						*
														4	0	x1	50
x2		2
										x1 x2 x3
																*	25
L		1								x1 x2						x2
															0	x*	100
x3		2								x1 x2 x3						3
L			2x1							4x1 x3					300	0

Гранична норма заміни другого товару першим:

dx			U	x	2		x*
	1					1		2	,
dx	2		U	x			x*
					1	2

тобто, для заміни одиниці другого товару необхідно 2 одиниці першого.

Тепер розглянемо задачу у сфері виробництва [1]. Виробник розв’язує основну задачу максимізації прибутку, тобто максимального випуску за визначених витрат, а також мінімізацію витрат за визначеного об’єму випуску.

Нехай виробнича фірма випускає один продукт.

27

Річний випуск позначимо через У. Можливі витрати різних видів ресурсів

		x1
	позначимо через вектор-стовпчик X	x2	.
		...

xn

Тоді технологія фірми визначається її виробничою функцією: y F(X )

Нехай W w1 , w2 ,...,wn - вектор-рядок цін ресурсів, р – ціна продукції. Тоді кожному вектору витрат Х відповідає прибуток:

П( Х ) рF( X ) WX ,

(50)

де pF(X ) py R – річний дохід фірми,

WX c –витрати виробництва за рік.

Якщо не вводити ніяких обмежень, окрім невід’ємності витрат, то задача на максимум прибутку виглядає так:

max pF ( X ) WX .	(51)
X 0
Це задача математичного програмування з n умовами: xi	0 i 1, n .

Необхідними умовами її розв’язування є умови Куна-Таккера:

	П		p	F		W		0
	Х			X						.	(52)
	П					F
		X		p				W X 0,	X	0
	Х					X
Якщо використовуються всі ресурси, тобто X *									0 ,	то ці	умови мають

вигляд:

	F X *			F X	*
p		W	p			w , i 1, n			(53)
	X			xi		i
Таким чином, в оптимальній точці коштовність граничного продукту
даного ресурсу дорівнює його ціні.
Аналогічний за формою розв’язок має задача на максимум випуску за
заданих витрат:
		max F ( X ),
		WX	c,						(34)
		X	0
За допомогою функції Лагранжа
L(X , )		F(X ) (c		WX )					(55)

ця задача зводиться до задачі визначення максимуму, для якої умови КунаТаккера мають вигляд:

28

L

F

W

0

Х

X

,

(56)

L

F

X

W X 0, X 0

Х

X

звідки

F X *

F X *

W

wi , i 1, n .

(57)

X

xi

Розглянемо задачу максимізації обсягу продукції, що випускається, при обмеженні витрат на придбання ресурсів (факторів) у випадку двох ресурсів:

		f (x1, x2 )	max		(58)
за умови, що	p1x1	p2 x2 C ,	x1 0, x2	0 .	(59)
Розв’язування цієї задачі математичного програмування допускає наочну
геометричну інтерпретацію. Обмеженням відповідає трикутник					під прямою,
яка має рівняння p1x1	p2 x2	C , яке є ізокостою.		При максимізації функції

ізокванти пересуваються у "північно-східному" напрямку, поки вони мають загальні точки із зазначеним трикутником обмежень.

Геометричний розв’язок задачі очевидний: ізокванта та ізокоста, що відповідає фіксованим витратам виробництва С, будуть мати лише одну спільну точку B0 .

Координати x10 (C), x20 (C) точки B0 і дають розв’язок задачі.

Точка дотику залежить від значення витрат виробництва С. Безліч точок (x10 (C), x20 (C)) , що відповідають різним значенням витрат, утворять лінію L, що називається довгостроковою лінією розвитку фірми. Точка (x10 , x20 ) локальної ринкової рівноваги фірми обов'язково належить цій лінії.

29

x2

L

x0	(C)
2		B0
				Y Y3
				Y Y2
			Y	Y1
	0	(C)	p1x1 p2 x2 C	x
	x			1
	1

Рис. 2 Геометричний розв’язок задачі виробника

Таким чином, математично маємо задачу на умовний екстремум функції

f (x1, x2 )

max

за наявності обмежень:

p1x1

p2 x2

C ,

(60)

x1

0, x2

0 .

Поставлену задачу можна звести до задачі на безумовний екстремум

функції Лагранжа:

L(x1 , x2 ,

) f (x1 , x2 )

(C

p1 x1

p2 x2 ) .

(61)

Для функції

Лагранжа

запишемо

систему рівнянь (необхідні умови

існування безумовного екстремуму фунції кількох змінних)

L(x1 , x2 , )

0,

L(x1 , x2

, )

0,

L(x1 , x2

, )

0

x1

x2

або

f (x1, x2 )

p1,

f (x1, x2 )

p1,

C

p1x1

p2 x2 0 .

(62)

x1

x2

Розв'язавши

рівняння

щодо

шуканих змінних,

визначаємо

точку

(x10 (C), x20 (C)) , що є розв’язком оптимізаційної задачі. Підставляючи знайдені

значення факторів виробництва у виробничу функцію, отримаємо значення максимального випуску за заданих обмежень на витрати.

Приклад. Випуск фірми, що виробляє один продукт, задається виробничою функцією Кобба-Дугласа:

2 1

y F (K , L) 3K 3 L3 .

30