
- •Дифференциальное
- •Содержание
- •Вариант 1
- •Вариант 2
- •Вариант 3
- •Вариант 4
- •Вариант 5
- •Вариант 6
- •Вариант 7
- •Вариант 8
- •Вариант 9
- •Вариант 10
- •Вариант 11
- •Вариант 12
- •Вариант 13
- •Вариант 14
- •Вариант 15
- •Вариант 16
- •Вариант 17
- •Вариант 18
- •Вариант 19
- •Вариант 20
- •Вариант 21
- •Вариант 22
- •Вариант 23
- •Вариант 24
- •Вариант 25
- •Вариант 27
- •Вариант 28
- •Вариант 29
- •Вариант 30
- •2. Решение типового варианта по дифференциальному исчислению.
- •3. Варианты контрольных заданий по интегральному исчислению. Вариант 1
- •Вариант 2
- •Вариант 3
- •Вариант 4
- •Вариант 5
- •Вариант 6
- •Вариант 7
- •Вариант 8
- •Вариант 9
- •Вариант 10
- •Вариант 11
- •Вариант 12
- •Вариант 13
- •Вариант 14
- •Вариант 15
- •Вариант 16
- •Вариант 17
- •Вариант 18
- •Вариант 19
- •Вариант 20
- •Вариант 21
- •Вариант 22
- •Вариант 23
- •Вариант 24
- •Вариант 25
- •Вариант 26
- •Вариант 27
- •Вариант 28
- •Вариант 29
- •Вариант 30
- •4. Решение типового варианта
2. Решение типового варианта по дифференциальному исчислению.
1. Вычислить пределы с помощью правила Лопиталя:


Это есть
неопределённость вида
![]() Обозначив выражение под знаком пре-
Обозначив выражение под знаком пре-
дела через
![]() рассмотрим
рассмотрим

Значит,
![]() .
.
2. Провести
исследование и настроить график функции:
![]()
Область
определения:
![]() функция является нечетной; она непрерывна
функция является нечетной; она непрерывна
для всех
![]() ,
поэтому её график вертикальных асимптот
не имеет; наклонные и
,
поэтому её график вертикальных асимптот
не имеет; наклонные и
горизонтальные асимптоты:

т.е. при
![]() асимптотой является прямая
асимптотой является прямая![]() а при
а при![]()
асимптотой
является прямая
![]()

Далее имеем:
 знаки
знаки
![]()
![]()
![]()
![]()
т.е. функция
возрастает на интервалах
![]() и
и![]() и убывает на интер-
и убывает на интер-
вале
![]()
![]() является точкой максимума, а
является точкой максимума, а![]() является
точкой мини-
является
точкой мини-
мума:

 знаки
знаки
![]()
![]() т.е. график функции будет выпуклым
на
т.е. график функции будет выпуклым
на
![]()
интервале
![]() ,
и вогнутым на интервале
,
и вогнутым на интервале![]() точка
точка![]() будет точкой
будет точкой
перегиба графика;
![]() График функции будет иметь вид:
График функции будет иметь вид:

![]()
![]()
![]()
![]()
![]()
![]()
3. Построить график
функции в полярной системе координат:
![]()
График строится
“по точкам” с учетом того, что
![]() возрастает при
возрастает при
![]() то есть при
то есть при
![]() и убывает при
и убывает при![]() то есть при
то есть при
![]()


![]() и так далее. В
итоге, график будет иметь вид:
и так далее. В
итоге, график будет иметь вид:

4. Найти радиус основания и высоту конуса наименьшего объема, описан-
ного около сферы
единичного радиуса.
![]() .
.
Из
подобия треугольников
![]()
![]()

![]() т.к.
т.к.![]() то отсюда
то отсюда
![]()
![]()

О
Теперь
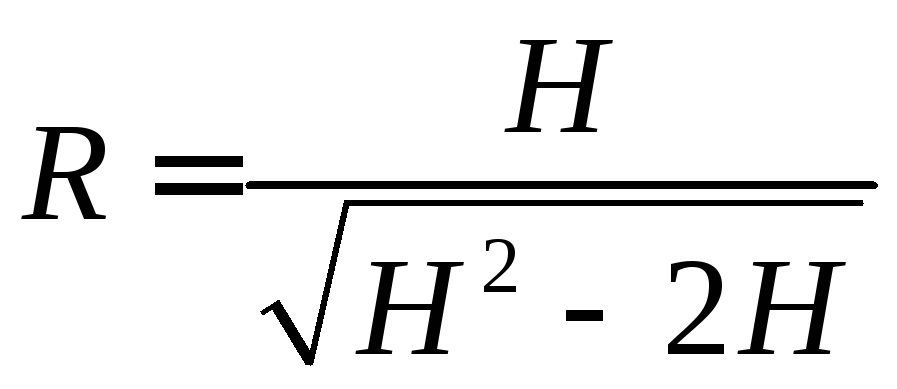
![]()
![]()
![]()
и
 где
где![]()
Найдем, при каком
![]() эта функция будет наименьшей:
эта функция будет наименьшей:
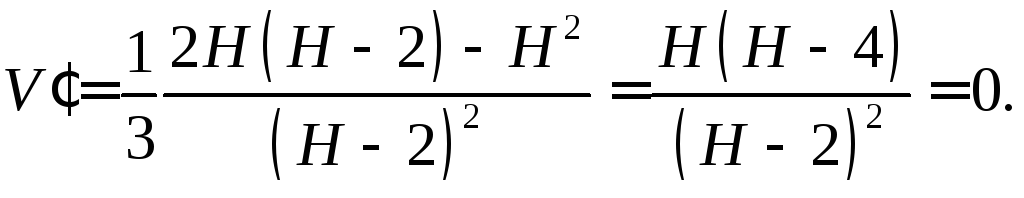 т.к.
т.к.
![]() то отсюда
то отсюда![]()
 Знаки
Знаки
![]()
![]()
![]()
![]()
Значит,
![]() убывает на
убывает на![]() и возрастает на
и возрастает на![]() и функция будет
и функция будет
наименьшей при
![]() Тогда
Тогда![]()
![]()
 Таким
Таким
образом,
![]()
5. Вычислить
![]() функции
функции .
Разделим числитель на знаменатель
.
Разделим числитель на знаменатель
и разложим оставшуюся правильную дробь на простые:

при
![]() отсюда
отсюда![]() при
при![]() отсюда
отсюда![]()
Таким образом,
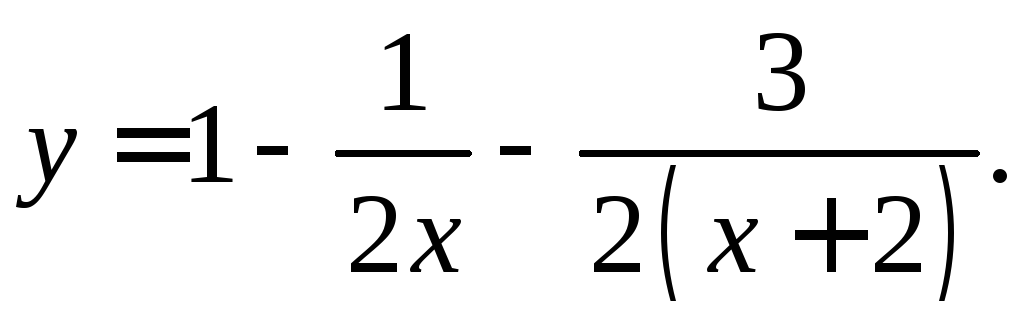 Теперь легко найти искомую произ-
Теперь легко найти искомую произ-
водную:

Теперь вычислим
![]() функции
функции![]() .
.
Используя
формулу Лейбница при
![]() имеем:
имеем:
![]() (все остальные
члены будут равны
(все остальные
члены будут равны
![]() );
);
![]()
6. Используя
формулу Тейлора 2-ого порядка, вычислить
приближенно
![]() и
и
доказать, что
при этим погрешность
![]() допускает оценку
допускает оценку![]()

Далее используем
формулу

в которой
![]()

![]() между
между
![]() и
и![]() Отбрасывая остаточный член
Отбрасывая остаточный член![]() имеем приближенно
имеем приближенно

Погрешность
этих вычислений допускает оценку
 т.к.
т.к.
наибольшее значение этой дроби будет при наименьшем её знаменателе,
т.е. при
![]() .
.
7. Составить
уравнения касательной и нормали к кривой

в точке
![]() и вычислить
и вычислить![]()

Уравнение
касательной имеет вид

Уравнение
нормали имеет вид

Далее имеет:

 .
.
8. Вычислить
производную 2-го порядка от неявной
функции:
![]() ,
т.е.
,
т.е.
![]() дифференцируем
это равенство по
дифференцируем
это равенство по
![]()
откуда

Дифференцируем
это равенство по
![]() еще раз:
еще раз:
 .
.
9. Вычислить предел
с помощью формулы Тейлора:

Это есть
неопределённость вида
![]()
Обозначим
![]() тогда наш предел будет равен
тогда наш предел будет равен
 что в силу 1-ого
что в силу 1-ого
замечательного
предела
![]() приводит к
приводит к Далее используем готовые
Далее используем готовые
разложения
 и
и подставляя в
подставляя в
них вместо
![]() соответственно, получим
соответственно, получим

Теперь исходный предел будет равен

поскольку последний предел, согласно определению бесконечно малой
более высокого
порядка, равен
![]() то получаем ответ:
то получаем ответ:![]()
10. Написать формулу
Лагранжа для функции
 и найти
и найти
соответствующую
точку
![]()
Формула
Лагранжа имеет вид
 для нашей
для нашей
функции будем
иметь
 т.е.
т.е.![]() и
и![]()
11. По графику функции построить график её первой производной. Под
графиком функции будем строить график её производной, учитывая что:
- на интервалах
возрастания функции
![]() и
и![]() её производная
её производная
положительна,
а на интервале убывания
![]() это производная отрица-
это производная отрица-
тельна;
-точки
![]() и
и![]() являются точками экстремума функции,
значит производная
являются точками экстремума функции,
значит производная
функции в этих
точках равна
![]() или не существует:
или не существует:![]() не
не
существуют, т.к. в этой график функции имеет вертикальную касательную,
а в силу того, что производная – это угловой коэффициент касательной,
![]()
- аналогично, т.к. график функции имеет вертикальную касательную и в
точке
![]() ,
то в этой точке производная также имеет
бесконечный разрыв;
,
то в этой точке производная также имеет
бесконечный разрыв;
- т.к. при
![]() график функции имеет асимптоту
(предположительно
график функции имеет асимптоту
(предположительно
![]() ),
то график её производной будет иметь
горизонтальную асимптоту
),
то график её производной будет иметь
горизонтальную асимптоту
![]() т.е.
т.е.
![]()

Рис. 1.

Рис. 2.
