2.3.7. Гармонический осциллятор

Гармонические колебания можно представить несколькими способами. Рассмотрим эти способы.

•Аналитический:

x = A sin ( ω t + φ0 ); υx = υm cos ( ω t + φ0 ); ax = –am sin ( ω t + φ0 ).

•Графический.

•Геометрический, с помощью вектора амплитуды (метод векторных диаграмм):

Рассмотрим подробнее последний способ.

Пусть гармоническое колебание описывается уравнением x = A cos ( ω t + φ0 ).

Проведем прямую Оx (опорную) и построим вектор , направленный из точки О под углом φ0 к опорной линии.

Обозначим через x0 проекцию вектора	на опорную линию в момент времени
t = 0:
x0 = A cos ( φ0 ).

Вращение происходит против часовой стрелки, т.е. ω > 0. За промежуток времени t вектор амплитуды повернется на угол ωt и займет новое положение. Его проекция на опорную линию равна x = A cos ( ω t + φ0 ).

За время, равное периоду колебаний Т, вектор амплитуды повернется на угол 2φ , и проекция вектора совершит полное колебание около положения равновесия (точка О). Следовательно, вращающийся вектор амплитуды полностью характеризует гармоническое колебание.

Проекция кругового движения на ось у также совершает гармоническое колебание y = A sin ( ω t + φ ).

Таким образом, равномерное движение по окружности можно рассматривать как два колебательных гармонических движения, совершаемых одновременно в двух взаимно перпендикулярных направлениях. Этим представлением широко пользуются при сложении колебаний.

156

2.3.8. Сложение гармонических колебаний одного направления и одинаковой частоты. Биения

Пусть точка одновременно участвует в двух гармонических колебаниях одинакового периода, направленных вдоль одной прямой.

Сложение колебаний будем проводить методом векторных диаграмм (рис. 2.3.8). Пусть колебания заданы уравнениями

и

(2.3.21)

Рис. 2.3.8 Сложение колебаний методом векторных диаграмм

Отложим из точки О вектор под углом φ1 к опорной линии и вектор 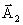под углом φ2. Оба вектора вращаются против часовой стрелки с одинаковой угловой скоростью ω,

поэтому их разность фаз не зависит от времени (	). Такие колебания
называют когерентными.

Нам известно, что суммарная проекция вектора равна сумме проекций на эту же ось. Поэтому результирующее колебание может быть изображено вектором амплитуды , вращающимся вокруг точки О с той же угловой скоростью ω, что и , и

. Результирующее колебание должно быть также гармоническим с частотой ω:

.

По правилу сложения векторов найдем суммарную амплитуду:

157

Результирующую амплитуду найдем по формуле

. (2.3.22)

Начальная фаза определяется из соотношения

(2.3.23)

.

Таким образом, тело, участвуя в двух гармонических колебаниях одного направления и одинаковой частоты, совершает также гармоническое колебание в том же направлении и с той же частотой, что и складываемые колебания.

Из (2.3.22) следует, что амплитуда А результирующего колебания зависит от разности начальных фаз . Возможные значения А лежат в диапазоне

(амплитуда не может быть отрицательной).

Рассмотрим несколько простых случаев.

1.Разность фаз равна нулю или четному числу π, то есть , где

. Тогда и

,	(2.3.24)
так как	, т.е. амплитуда результирующего

колебания А равна сумме амплитуд складываемых колебаний (колебания синфазны) (рис.

2.3.9).

158

Рис. 2.3.9

2. Разность фаз равна нечетному числу π, то есть , где

. Тогда . Отсюда

. (2.3.25)

На рис. 2.3.10 изображена амплитуда результирующего колебания А, равная разности амплитуд складываемых колебаний (колебания в противофазе).

Рис. 2.3.10

3. Разность фаз изменяется во времени произвольным образом:

(2.3.26)

Из уравнения (2.3.26) следует, что и будет изменяться в соответствии с

величиной

. Поэтому при сложении некогерентных колебаний не имеет

смысла говорить о сложении амплитуд, но в некоторых случаях наблюдаются вполне определенные закономерности. Для практики особый интерес представляет случай, когда два складываемых колебания одинакового направления мало отличаются по частоте. В результате сложения этих колебаний получаются колебания с периодически изменяющейся амплитудой.

Периодические изменения амплитуды колебания, возникающие при сложении двух гармонических колебаний с близкими частотами, называются биениями. Строго говоря,

это уже не гармонические колебания.

Пусть амплитуды складываемых колебаний равны А, а частоты равны ω и		,
причем	. Начало отсчета выбираем так, чтобы начальные фазы обоих колебаний
были равны нулю:

159

Сложим эти выражения, пренебрегая	, так как
	.

(2.3.27)

.

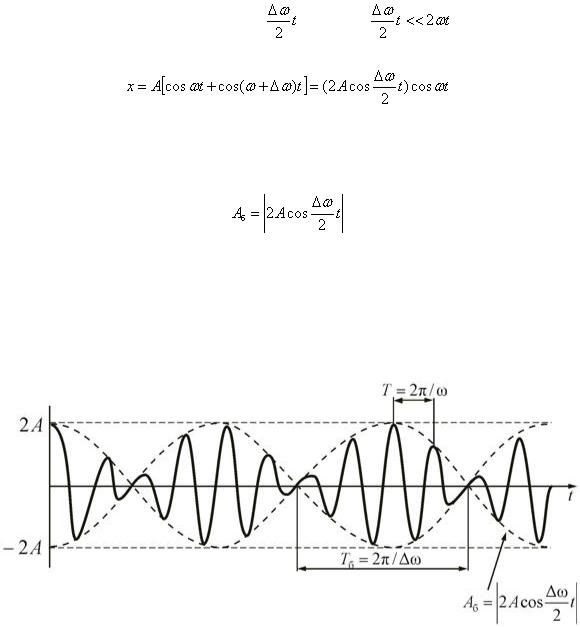
Результирующее колебание (2.3.27) можно рассматривать как гармоническое с частотой ω и амплитудой Аб, которая изменяется по следующему периодическому закону:

(2.3.28)

;

.

Характер зависимости (2.3.28) показан на рис. 2.3.11, где сплошные жирные линии дают график результирующего колебания, а огибающие их – график медленно меняющейся по уравнению (2.3.27) амплитуды.

Рис. 2.3.11

Определение частоты тона (звука определенной высоты) биений между эталонным и измеряемым колебаниями – наиболее широко применяемый на практике метод сравнения измеряемой величины с эталонной. Метод биений используется для настройки музыкальных инструментов, анализа слуха и т.д.

Вообще, колебания вида называются модулированными.

Частные случаи: амплитудная модуляция и модулирование по фазе или частоте. Биение – простейший вид модулированных колебаний.

Любые сложные периодические колебания можно представить в виде

суперпозиции одновременно совершающихся гармонических колебаний с различными амплитудами, начальными фазами, а также частотами, кратными циклической частоте ω:

160

.

Представление периодической функции в таком виде связывают с понятием

гармонического анализа сложного периодического колебания, или разложения Фурье (то есть представление сложных модулированных колебаний в виде ряда (суммы) простых гармонических колебаний). Слагаемые ряда Фурье, определяющие гармонические колебания с частотами ω, 2ω, 3ω, ..., называются первой (или основной), второй, третьей

и т.д. гармониками сложного периодического колебания.

161