ЛЕКЦИЯ 21

2.3.9. Сложение взаимно перпендикулярных колебаний

Пусть некоторое тело колеблется и вдоль оси x, и вдоль оси y, т.е. участвует в двух

взаимноперпендикулярных колебаниях:
;	.	(2.3.29)
Найдем уравнение результирующего колебания. Для простоты примем			.
Разность фаз между обоими колебаниями равна:		.
Чтобы получить уравнение траектории, надо исключить из этих уравнений время t.
Упростим выражения, выбрав начало отсчета так, чтобы		, т.е.
;		.

или

.

Распишем второе уравнение через косинус суммы:

	.
Отсюда	.
Возведем обе части в квадрат:

;

.

162

Окончательное уравнение:

(2.3.30)

.

В результате мы получили уравнение эллипса, оси которого ориентированы относительно x и y произвольно (рис. 2.6).

Рис. 2.3.12

2.3.10. Фигуры Лиссажу

Рассмотрим некоторые частные случаи решений уравнения (2.3.30).

1. Начальные фазы колебаний одинаковы:

т.е.

Тогда уравнение (2.3.30) примет вид:

или ;

отсюда получим уравнение результирующего колебания:

(2.3.31)

Это уравнение прямой, проходящей через начало координат (рис. 2.3.13, а).

Следовательно, в результате сложения двух взаимно перпендикулярных колебаний с одинаковыми начальными фазами будут происходить колебания вдоль прямой, проходящей через начало координат.

163

а

б

в

Рис. 2.3.13

Такие колебания называются линейно поляризованными.

2. Начальная разность фаз равна π. Тогда , следовательно

;

.

Уравнение колебания в этом случае

(2.3.32)

То есть точка тоже будет колебаться вдоль прямой, проходящей через начало координат, но прямая лежит в других четвертях по сравнению с первым случаем (рис.

2.3.13, б).

Амплитуда результирующего колебания в обоих случаях равна:

. (2.3.33)

3. Начальная разность фаз равна π/2. Проанализируем уравнение (2.3.30), учитывая,

что

.

(2.3.34)

.

164

Это уравнение эллипса с полуосями А1 и А2 (рис. 2.3.13, в). Случай эллиптически

поляризованных колебаний.

При	получим уравнение окружности (циркулярно-поляризованные

колебания).

4. Все остальные разности фаз дают эллипсы с различным углом наклона относительно осей координат.

Необходимо отметить, что все рассматриваемые случаи, все	кривые – это эллипсы
(даже прямая – частный случай эллипса).

Фигуры, получаемые при сложении взаимно перпендикулярных колебаний разных частот, называются фигурами Лиссажу (Ж. Лиссажу (1822–1880) – французский физик). В простейших случаях можно сравнить частоты по виду фигур.

В приведенных выше примерах рассматривались простейшие случаи, когда Если , то в результате будут получаться уже не эллипсы, а более

сложные фигуры Лиссажу.

2.3.11. Свободные затухающие механические колебания

Все реальные колебания являются затухающими. Энергия механических колебаний постепенно расходуется на работу против сил трения и амплитуда колебаний постепенно уменьшается (затухает).

Во многих случаях в первом приближении можно считать, что при небольших скоростях силы, вызывающие затухание колебаний, пропорциональны величине скорости (например маятник). Тогда сила трения (или сопротивления)

,

где r – коэффициент сопротивления, – скорость движения.

Запишем второй закон Ньютона для затухающих прямолинейных колебаний вдоль оси

x:

,

где kx – возвращающая сила, rυx – сила трения. Это уравнение можно переписать:

, отсюда следует:

.

Введем обозначения: ; .

Тогда однородное дифференциальное уравнение второго порядка, описывающее затухающее колебательное движение, запишем так:

165

(2.3.35)

.

Решение уравнения (2.3.35) имеет вид (при ):

. (2.3.36)

Здесь А0 и φ0 определяются из краевых условий задачи (начальных и граничных), а β и ω – из самого уравнения.

Найдем круговую частоту ω. Здесь она уже не равна .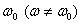

Для этого найдем первую и вторую производные от x:

,

Подставим эти значения в (3.1.1) и сократим на :

.

Сократим на и выразим ω:

,

,

где ω0 – круговая частота собственных колебаний (без затухания); ω – круговая частота свободных затухающих колебаний. Из этого выражения ясно, почему решение

(2.3.35) будет только при .

Для колебаний под действием различных сил (квазиупругих) значения ω, β, ω0 будут различными. Например, для колебаний под действием упругой силы

; ;

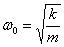166