ЛЕКЦИЯ 4

2.1.13. Связь между напряженностью и потенциалом

Разные пробные заряды q',q'',… будут обладать в одной и той же точке поля разными

энергиями W', W'' и так далее. Однако отношение

будет для всех зарядов одним и

тем же. Поэтому можно вести скалярную величину, являющуюся энергетической характеристикой собственно поля – потенциал:

(2.1.48)

Из этого выражения следует, что потенциал численно равен потенциальной энергии, которой обладает в данной точке поля единичный положительный заряд.

Подставив в (2.1.48) значение потенциальной энергии (2.1.46), получим для потенциала точечного заряда следующее выражение:

(2.1.49)

Потенциал, как и потенциальная энергия, определяют с точностью до постоянной интегрирования. Поскольку физический смысл имеет не потенциал, а разность потенциалов, поэтому договорились считать, что потенциал точки, удаленной в бесконечность, равен нулю. Когда говорят «потенциал такой-то точки» – имеют в виду

разность потенциалов между этой точкой и точкой, удаленной в бесконечность. Другое определение потенциала:

,

т.е. потенциал численно равен работе, которую совершают силы поля над единичным положительным зарядом при удалении его из данной точки в бесконечность (или наоборот – такую же работу нужно совершить, чтобы переместить единичный

положительный заряд из бесконечности в данную точку поля). При этом	, если q >
0.

Если поле создается системой зарядов, то, используя принцип суперпозиции, получаем:

(2.1.50)

Тогда и для потенциала 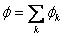или

,

(2.1.51)

36

т.е. потенциал поля, создаваемый системой зарядов, равен алгебраической сумме потенциалов, создаваемых каждым из зарядов в отдельности. А вот напряженности складываются при наложении полей – векторно. По этой причине потенциалы полей считать проще, чем напряженности.

Вернемся к работе сил электростатического поля над зарядом q. Выразим работу через разность потенциалов между начальной и конечной точками:

(2.1.52)

Таким образом, работа над зарядом q равна произведению заряда на убыль потенциала. То есть

(2.1.53)

где U – напряжение.

(Здесь видна хорошая аналогия с гравитационным полем:

,

здесь gh – имеет смысл потенциала, а m – заряда гравитационного поля).

Итак, потенциал – скалярная величина, поэтому пользоваться и вычислять φ проще, чем E . Приборы для измерения разности потенциалов широко распространены.

Формулу

можно использовать для установления единиц потенциала: за

единицу φ принимают потенциал в такой точке поля, для перемещения в которую из бесконечности единичного положительного заряда необходимо совершить работу равную единице.

ВСИ – единица потенциала .

Вфизике часто используется единица энергии и работы, называемая электрон - вольт

(эВ) – это работа, совершенная силами поля над зарядом, равным заряду электрона при прохождении им разности потенциалов 1 В, то есть:

Итак, электростатическое поле можно описать либо с помощью векторной величины E , либо с помощью скалярной величины φ. Очевидно, что между этими величинами должна существовать определенная связь. Найдем ее:

Изобразим перемещение заряда q по произвольному пути l (Рис. 2.1.28) в электростатическом поле E .

37

Работу, совершенную силами электростатического поля на бесконечно малом отрезке dl, можно найти так:

(2.1.54)

где El – проекция E на ; dl– произвольное направление перемещения заряда.

С другой стороны, как мы показали, эта работа, если она совершена электростатическим полем, равна убыли потенциальной энергии заряда, перемещенного на расстоянии dl:

,

отсюда

(2.1.55)

Для ориентации dl (направление перемещения) в пространстве, надо знать проекции E на оси координат:

(2.1.56)

По определению градиента сумма первых производных от какой-либо функции по координатам есть градиент этой функции, то есть

– вектор, показывающий направление наибыстрейшего увеличения

функции.

Тогда коротко связь между E и φ записывается так:

(2.1.57)

или так:

,

(2.1.58

где (набла) означает символический вектор, называемый оператором Гамильтона.

38

Знак минус говорит о том, что вектор E направлен в сторону уменьшения потенциала электрического поля.

2.1.14. Безвихревой характер электростатического поля

Из условия	следует одно важное соотношение, а именно, величина, векторного
произведения	для стационарных электрических полей всегда равна нулю.

Действительно, по определению, имеем

,

поскольку определитель содержит две одинаковые строки.

Величина , называется ротором или вихрем и обозначается, как rot E.

Мы получаем важнейшее уравнение электростатики:

rot E.

(2.1.59)

Таким образом кулоновское электростатическое поле – безвихревое.

Согласно теореме Стокса, присутствует следующая связь между контурным и поверхностным интегралами:

,

где контур L ограничивает поверхность S, ориентация которой определяется направлением вектора положительной нормали n:

.

Поэтому работа при перемещении заряда по любому замкнутому пути в электростатическом поле равна нулю.

Это условие выполняется для любой радиальной силы независимо от показателя степени n.

2.1.15. Силовые линии и эквипотенциальные поверхности

39

Направление силовой линии (линии напряженности) в каждой точке совпадает с

направлением E . Отсюда следует, что напряженность E равна разности потенциалов U на единицу длины силовой линии.

Именно вдоль силовой линии происходит максимальное изменение потенциала.

Поэтому всегда можно определитьE между двумя точками, измеряя U между ними, причем тем точнее, чем ближе точки. В однородном электрическом поле силовые линии –

прямые. Поэтому здесь определить E наиболее просто:

(2.1.60)

.

Теперь дадим определение эквипотенциальной поверхности. Воображаемая

поверхность, все точки которой имеют одинаковый потенциал, называется эквипотенциальной поверхностью. Уравнение этой поверхности

(2.1.61)

Графическое изображение силовых линий и эквипотенциальных поверхностей показано на рисунке 2.1.30.

Рис. 2.1.30. Графическое изображение силовых линий и эквипотенциальных поверхностей

При перемещении по этой поверхности на dl потенциал не изменится:

Отсюда следует, что проекция вектора E на dl равна нулю, то есть

Следовательно, E в каждой точке направлена по нормали к эквипотенциальной поверхности.

Эквипотенциальных поверхностей можно провести сколько угодно много. По густоте эквипотенциальных поверхностей можно судить о величине E , это будет при условии,

40