
- •Предисловие
- •Список использованных сокращений
- •Часть 1.
- •Глава 1. Математические основы формализации и методов описания
- •Часть 2.
- •Глава 2. Методы представления знаний с использованием
- •Часть 3.
- •Глава 3. Интеллектуальные технологии создания информационных систем. Способы получения информации и ее реализации для оценивания состояния агрегатов
- •Часть 4.
- •Глава 4. Источники информации и причины возникновения ее неопределенности
- •4.1. Переработка и использование информации в реальных условиях функционирования агрегатов
- •Часть 5.
- •Список использованных сокращений и обозначений
- •Введение:
- •Часть 1.
- •Глава 1. Математические основы формализации и методов описания
- •Формализация объекта и парадигмы
- •1.3. Множества и перечень базовых операций над множествами
- •Перечень базовых операций над множествами
- •Области определения функций
- •Обратная функция
- •Теорема
- •Мера и нечеткая мера
- •Задача построения нечетких мер
- •Нечеткие множества: определение и формы записи в операциях и
- •1.7.Функции доверия и правило Демпстера а.Р.,[23]
- •1.8. Нормировка функций в теории нечётких множеств
- •1.9. Нечёткие отношения: прямая и обратная задачи
- •Глава 2. Методы представления знаний с использованием приближенных и нечетких множеств
- •2.1.Нечеткие вычислительные технологии
- •2.2.Семантика объекта: определение и типизация
- •2.3.Создание Базы знаний: постановка, семантика, прагматика
- •2.4. Сопоставление объектов: постановка, семантика, прагматика
- •2.5.Распознавание объектов: постановка, семантика, прагматика
- •2.6. Управление процессом представления знаний
- •Нечёткие множества: субъективность и неточность
- •2.8.Нечеткая алгебра
- •2.9.Нечеткие иерархические отношения
- •2.10.Естественность операций max и min
- •2.11.Нечеткая статистика
- •2.12. Совместимость и нечеткое ожидание
- •Глава 3. Нечеткие технологии создания информационных систем. Способы получения информации и ее реализации для оценивания состояния агрегатов
- •3.2. Обработка нечетких данных как неопределенных чисел
- •Методология представления агрегата в виде комплексного механизма
- •3.2.2. Описание исходной информации на языке размытых множеств
- •Размытость интервалов, ограничений, критериев и целей управления в эксплуатации и диагностике
- •3.3.3. Размытые ограничения, цели и оптимизация работы агрегата в условиях нечеткой информации о состоянии
- •Анализ информации для диагностики и оценивания состояния механизмов
- •3.5. Оценки погрешностей измерений и наблюдений за состоянием агрегатов
- •Влияние погрешностей исходных данных на погрешности диагноза
- •Глава 4. Источники информации и причины возникновения ее неопределенности
- •4. 2. Управление и идентификация на объекте в условиях неопределенности информации на основе знаний, получаемых при функциональной диагностике
- •Тогда множество диагностических признаков g также будет нечетким
- •4.3.Представление и использование чётких и «размытых» знаний в математических моделях оценивания состояния агрегатов, на основе функциональной диагностики
- •4.3.1.Формализация решения задачи оценивания состояния
- •4.3.2. Особенности решения задач контроля и функционирования агрегата
- •Глава 5. Введение в генетическое программирование
- •5.1. Введение в генетические и эволюционные алгоритмы
- •5.2. Сравнительный анализ эволюционных алгоритмов
- •5.3. Генетическое программирование
- •5.4. Перспективные направления развития гп
- •Глава 6. Введение в нейронные сети
- •6.1. Алгоритмы их обучение и эластичные нейро-нечеткие системы
- •6.2. Имитация нервных клеток
- •6.3. Математическая модель нейрона
- •6.4. Обучение нейронных сетей
- •6.5. Метод обратного распространения ошибки
- •6.6. Алгоритм настройки нейронной сети
- •Глава 7. Другие методы нечетких технологий для построения
- •7.1. Введение в теорию возможностей и смысла
- •7.1.1. Неопределенность и неточность
- •7.1.2. Традиционные модели неточности и неопределенности
- •7.1.3. Меры неопределенности
- •7.1.4. Меры возможности и необходимости
- •7.1.5. Возможность и вероятность
- •7.2. Языки и технологии логического программирования prolog, lisp
- •Глава 8. Послесловие
- •8.1. Эволюция искусственного интеллекта для развития интеллектуальных
- •8.2.Экспертные системы нового уровня
- •8.3. Роботика
- •8.4. Преобразование речи искусственного языка
- •8.5. Интеллект муравьёв и его использование
- •8.6. Искусственная жизнь, мозг, познание, разум, память и мышление
- •8.7. Боты
- •Optimizator подсистемы диагностики состояния энергоустановок, skais, для решения задач технического обслуживания
- •Заключение
- •Заключение
- •Литература
1.3. Множества и перечень базовых операций над множествами
Множества
по Г. Кантору есть совокупность однородных
сущностей, называемых элементами.
Например, если множество A
состоит из элементов ,
в котором
,
в котором
 А,
А,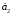
 А,
А,
 А,
то А =
А,
то А = .
.
Число
элементов множества
 называется мощностью или кардинальным
числом и обозначается#А.
Например,
если А =
называется мощностью или кардинальным
числом и обозначается#А.
Например,
если А =
 ,
то#А
= 3,
т.е. обладающих совокупностью однородных
сущностей (мощность множества, или любой
объект в предметной области).
,
то#А
= 3,
т.е. обладающих совокупностью однородных
сущностей (мощность множества, или любой
объект в предметной области).
Подмножества
множества
 -
любое множество, каждый элемент которого
принадлежит
-
любое множество, каждый элемент которого
принадлежит .
Например, если А =
.
Например, если А =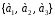 ,
то подмножествамиА
являются
,
то подмножествамиА
являются
{ },
{
},
{ },
{
},
{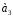 },
{
},
{ },
{
},
{ },
{
},
{ }
и
}
и .
Каждое
из них вложено в множество А,
например,
{
.
Каждое
из них вложено в множество А,
например,
{ }
вложено в А,
или {
}
вложено в А,
или { }
} .
.
Аксиома 1: пустое множество, обозначаемое { } или Ø, имеет свойства:
{ }
 А ≠ Ø (пустое множество есть подмножество
всякого не пустого множества);
А ≠ Ø (пустое множество есть подмножество
всякого не пустого множества);{Ø} ≠ Ø, (множество, состоящее хотя бы из одного элемента Ø, не является пустым).
Пространство – это множество всех элементов, которые могут встретиться в нашем исследовании.
Универсальное
множество
(полное пространство) будем записывать
следующим образом:
 гдеi
- есть подмножество элементов,
гдеi
- есть подмножество элементов,
 .
.
Множество
действительных чисел будем обозначать
как
 .
.
Характеристическая функция множества А:
 (1.2)
(1.2)
Степенное множество: 2X, есть множество всех подмножеств универсального множества X. Например, если X = {x1, x2, x3}, то
2X= {{x1}, {x2}, {x3}, {x1,x2}, {x1, x3}, {x2,x3}, {x1,x2,x3}}.
Множества типизированы как счетные и несчетные, конечные и бесконечные.
Аксиома
2: множество натуральных чисел
 является
счетным и называется аксиоматическим
эталоном.
является
счетным и называется аксиоматическим
эталоном.
Счетность некоторого множества определяется путем установления его взаимного и однозначного соответствия с эталоном, а при нарушении этого соответствия – множество будет несчетным.
Конечность некоторого множества определяется по его конечной мощности. Установление бесконечности требует привлечения теории Г. Кантора [1].
Перечень базовых операций над множествами
Дополнение ¬А. Если X={x1, x2, x3} и A={x1, x2}, то ¬А={x3};
Разность А\В. Если A={x1, x2} и B={x2, x3}, то А\В = {x1};
Пересечение (произведение)
 если
если
 и
и ,
то
,
то ;
;Объединение (сумма)
 если
если
 и
и ,
то
,
то .
.
На
универсальном множестве X=
{ }
любое множествоА
можно записать так:
}
любое множествоА
можно записать так:
 ,
(1.3)
,
(1.3)
где
 принимает все значения из подмножества
принимает все значения из подмножества множества натуральных чисел
множества натуральных чисел или
или -
множество номеров элементов
-
множество номеров элементов .
.
Например:
X
= { },
приi
от 1
до 10
и А
= {x1,
x4,
x6},
можно записать:
},
приi
от 1
до 10
и А
= {x1,
x4,
x6},
можно записать: ,
где
,
где принимает значения 1, 4, 6.
принимает значения 1, 4, 6.
Пусть задано универсальное множество, а в нем определено некоторое пространство, в котором имеется класс множеств.
Аксиома 3: класс множества пространства называется аддитивным, если:
всё пространство принадлежит классу;
все последовательности вложенных множеств из этого класса, их сумма и произведение принадлежат классу;
для множества и его подмножества из этого класса, и их разность - принадлежат классу.
Таким ообразом, признак аддитивности класса: счетное число операций сложения, умножения и вычитания над элементами этого класса, дают результат в том же классе. Например, если пространство равно {x1,x2}, то класс всех его возможных подмножеств есть множество подмножеств {{x1}, {x2}, {x1,x2}} или степенное множество в данном пространстве.
Проверим аддитивность этого класса. В соответствии с аксиомой 3, проверяем условия:
в классе множества {{x1}, {x2}, {x1, x2}}имеется элемент {x1, x2} равный пространству {x1,x2}, поэтому оно принадлежит классу {{x1}, {x2}, {x1, x2}};
б)
в классе {{x1},
{x2},
{x1,
x2}}
имеются две последовательности вложенных
множеств: {x1} {x1,
x2},
{x2}
{x1,
x2},
{x2} {x1,
x2},
в каждой из них сумма и произведение
множеств дают результат в том же классе;
{x1,
x2},
в каждой из них сумма и произведение
множеств дают результат в том же классе;
в)
в классе {{x1},
{x2},
{x1,
x2}}
имеются пары: множество и его подмножество
из того же класса -{x1,
x2} {x1},
{x1,
x2}
{x1},
{x1,
x2} {x2};
в каждой паре разность множества и
подмножества дают результат в том же
классе.
{x2};
в каждой паре разность множества и
подмножества дают результат в том же
классе.
Таким образом, условия а), б) и в) справедливы и класс {{x1}, {x2}, {x1, x2}} является аддитивным.
На
множестве действительных чисел R
определим интервалы как подмножество
 ,
гдеri
и
rj
– точная и неточная границы интервала
соответственно:
,
гдеri
и
rj
– точная и неточная границы интервала
соответственно:




ri rj
R
rj
R
Класс
всех интервалов
 на
множестве
на
множестве не является аддитивным, т.к. для вложенной
последовательности множеств, либо
множества и его подмножества, результат
суммы, либо разности, не будут принадлежать
исходному классу (не выполняется условие
б) или в) аксиомы 3.
не является аддитивным, т.к. для вложенной
последовательности множеств, либо
множества и его подмножества, результат
суммы, либо разности, не будут принадлежать
исходному классу (не выполняется условие
б) или в) аксиомы 3.
Например,
класс I1,
I2,
I3
является аддитивным, так как его элементы
не образуют вложенной последовательности
R
множеств, сумма которых даст результат
в том же классе { }:
}:






I1
I2
I3

не
является аддитивным, так как его элементы
не образуют вложенной последовательности
множеств, сумма которых даст результат
в том же классе
 .
.
Выполним
процедуру расширения класса интервалов
путём счётного повторения операций
сложения, вычитания и умножения над
элементами класса до тех пор, пока
расширенный класс не будет удовлетворять
условиям аддитивности, в соответствии
с аксиомой 3. Тогда вся совокупность,
полученных при расширении множеств,
называется классом борелевских множеств
[18]. Такой класс ещё называется борелевским
полем множеств, множествами, измеримыми
по Борелю или минимальной
 алгеброй
множеств. Будем обозначать этот класс
алгеброй
множеств. Будем обозначать этот класс .
.
Рассмотрим,
на примере, получение борелевского
класса. Пусть на множестве R
задан исходный класс интервалов { }:
}:




I1 I2 I3 R
Выполним
процедуру расширения класса { }
в класс {R1,
R2,
R3,
R4,
R5,
R6,
R7}
следующим образом:
}
в класс {R1,
R2,
R3,
R4,
R5,
R6,
R7}
следующим образом:

R1
= I1


R2
= I2

 R3
= I3
R3
= I3


R4
=



R5
=




R6
=



R7
=


Теперь проверим аддитивность полученного класса.
По аксиоме 3 условия аддитивности следующие:
в классе {R1÷R7} элементы R1, R2 и R3 равны элементам пространства I1, I2, I3 соответственно. Поэтому всё пространство
 принадлежит
классу
принадлежит
классу
{R1 R7};
R7};
в классе {R1÷R7} имеются шесть последовательностей вложенных множеств, каждое из которых сумма и произведение множеств дают результат в том же классе:
R1 R6
R6 R7;
R3
R7;
R3 R6
R6 R7;
R7;
R1 R4
R4 R7;
R2
R7;
R2 R4
R4 R7;
R7;
R3 R5
R5
 R7;
R2
R7;
R2 R5
R5 R7.
R7.
Например,
R1 R6
=
R6.
R6
=
R6.
в классе {R1÷R7} имеются пары: множество и его подмножество из того же класса, в каждой паре разность между множеством и подмножеством дает результат в том же классе: R4
 R1;
R4
R1;
R4 R2;
R5
R2;
R5 R2;
R5
R2;
R5 R3;
R6
R3;
R6 R3;
R7
R3;
R7 R6;
R7
R6;
R7 R4;
R7
R4;
R7 R5;
R7
R5;
R7 R1;
R7
R1;
R7 R2;
R7
R2;
R7 R3.
Например, R4
\ R1
=
R2.
R3.
Например, R4
\ R1
=
R2.
Таким образом, условия аддитивности выполняются и полученный класс – борелевский: В = {R1÷R7}.
