Численные методы решения обыкновенных дифференциальных уравнений Задача Коши для обыкновенного дифференциального уравнения

Постановка задачи. Пусть дано дифференциальное уравнение первого порядка

(1)

Требуется найти решение уравнения (1), удовлетворяющее начальным условиям

(2)

где ‑ заданные числа.

Задача Коши имеет единственное решение, удовлетворяющее условию (2), если функция непрерывна в некоторой окрестности точки и если в этой окрестности существует ограниченная частная производная .

Геометрически общее решение дифференциального уравнения (1) изображается в виде семейства интегральных кривых, лежащих в некоторой области на плоскости.

При выполнении выше сформулированных условий через точку плоскости будет проходить единственная интегральная кривая, которая и является решением задачи Коши.

Приближенные методы решения дифференциальных уравнений.

Большинство дифференциальных уравнений, с которыми приходится иметь дело на практике, может быть решено только с помощью приближенных методов, которые можно разбить на три вида:

а) аналитические, позволяющие получить приближенное решение в виде аналитического выражения;

б) графические, дающие возможность приближенного построения интегральной кривой;

в) численные, в результате применения которых, получается приближенное решение в виде таблицы значений искомой функции.

Рассмотрим лишь некоторые численные методы.

Численные методы решения дифференциальных уравнений

Метод Эйлера. Этот метод применяется в основном при проведении ориентировочных расчетов. Однако идеи, положенные в его основу, являются исходными при разработке многих других методов.

Пусть дано дифференциальное уравнение (1) и заданы начальные условия (2),

Требуется найти решение у= у(х) уравнения (1) на отрезке , удовлетворяющее условию (2).

Будем предполагать, что на отрезке [a; b], где ищется решение, выполнены все условия, обеспечивающие существование и единственность решения задачи Коши.

Разобьем отрезок [a; b] точками , где ‑ шаг интегрирования), на n равных отрезков.

Проинтегрируем уравнение (1) по отрезку

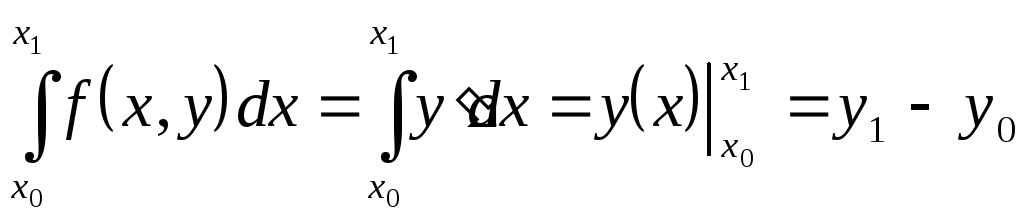
и получим:

.

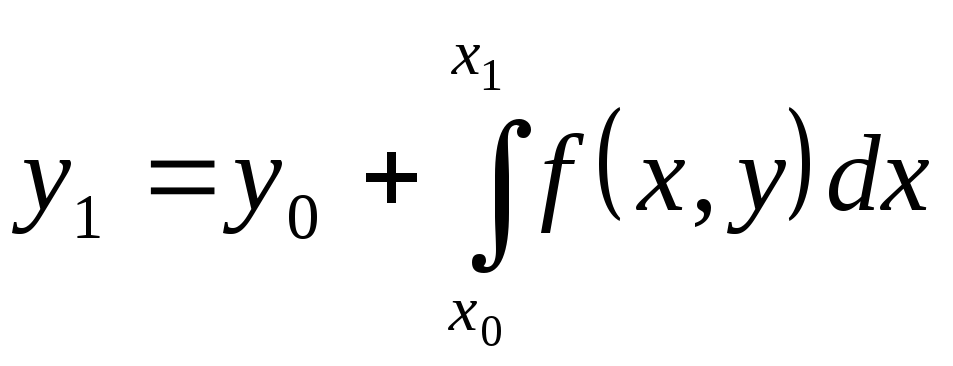Если шаг h достаточно мал, то можно считать, что

и тогда:

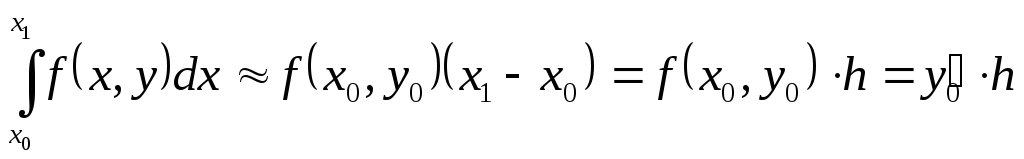
или ,

где

.

Точно так же, интегрируя по отрезку , получим:

, где .

Вообще:

,

где .

обозначим , тогда:

(3)

Реализация метода Эйлера сводится к последовательному вычислению разностей искомой функции и нахождению приближенных значений

в точках .

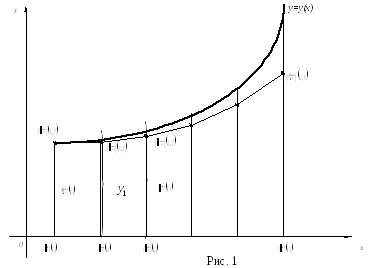
Геометрический смысл метода состоит в том, что интегральная кривая

заменяется приближенно ломаной , звенья которой имеют постоянную проекцию, равную h.

Первое звено будет касаться интегральной кривой в точке , остальные ‑ “соседних” интегральных кривых, проходящих через точки (рис. 1).

При вычислении последовательных значений

будет происходить накопление погрешностей, для приближенной оценки которых применяют двойной пересчет с шагом h и .

Если ‑ приближенное значение решения, полученное при расчете с шагом h

‑ улучшенное значение, полученное при шаге

и ‑ точное значение решения,

то абсолютную погрешность определяют из приближенного равенства

. (4)

Пример. Пусть дано уравнение

(5)

и заданы начальные условия .

Выберем шаг интегрирования h=0,2.

Результаты вычислений будем заносить в таблицу.

В первой строке (k=0) записываются начальные значения .

По ним вычисляют , а затем .

Тогда по формуле (3) при k=0, получим

.

Значения и записывают во второй сроке k=1.

Затем вычисляют:

и

.

По формуле (3) при k=1 получим:

.

Дальнейшие вычисления выполняются аналогично.

Таблица A

k						Точное решение
0	0,0	1,0000	0	1,0000	0,2000	1,0000
1	0,2	1,2000	0,3333	0,8667	0,1733	1,1832
2	0,4	1,3733	0,5928	0,7805	0,1561	1,3416
3	0,6	1,5315	0,7846	0,7458	0,1492	1,4832
4	0,8	1,6811	0,9532	0,7254	0,1451	1,6124
5	1,0	1,8269				1,7320

В последнем столбце таблицы приведены значения точного решения . Сравнивая результаты, замечаем, что погрешности вычисляемых значений решения возрастают. Абсолютная погрешность последнего значения составляет 0,0917, относительная погрешность равна примерно 5%.