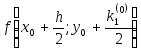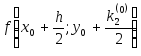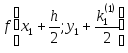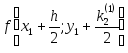Усовершенствованный метод Эйлера.
Пусть дано дифференциальное уравнение
(1) и заданы начальные условия (2). Требуется
найти решение уравнения (1) на отрезке
![]() .
Разобьем отрезок
.
Разобьем отрезок
![]() на n равных частей
точками
на n равных частей
точками
![]() ,
,
где
![]() ‑ шаг интегрирования.
‑ шаг интегрирования.
Суть усовершенствованного метода Эйлера состоит в следующем.
Найдем вспомогательное значение искомой функции
![]()
в промежуточной точке
![]() при помощи формулы
при помощи формулы
![]() . (6)
. (6)
Затем вычислим значение
![]() и, наконец, получим:
и, наконец, получим:
![]() . (7)
. (7)
Геометрический смысл решения иллюстрируется рисунком 2.


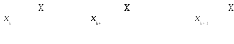
Пример. При помощи усовершенствованного метода Эйлера найдем решение уравнения
![]()
на отрезке
![]() ,
если известно, что
,
если известно, что
![]() а
а
![]() .
.
Результаты вычислений будем записывать в таблицу 2.
В первой строке таблицы
![]() записываем х0
=0, у0 = 1. Вычисляем: для
записываем х0
=0, у0 = 1. Вычисляем: для
![]() по формуле (6) находим
по формуле (6) находим
![]()
![]() .
.
Затем вычисляем
![]() и по формуле (7) имеем:
и по формуле (7) имеем:
![]() .
.
Во вторую строку таблицы
![]() записываем
записываем
![]() .
Дальнейшие вычисления проводятся
аналогично.
.
Дальнейшие вычисления проводятся
аналогично.
Таблица B
|
k |
|
|
|
|
|
|
Точное решение
|
|
0 |
0 |
1 |
0,1 |
0,1 |
1,1 |
0,1836 |
1,00 |
|
1 |
0,2 |
1,1836 |
0,0846 |
0,3 |
1,2682 |
0,1590 |
1,1832 |
|
2 |
0,4 |
1,3426 |
0,0747 |
0,5 |
1,4173 |
0,1424 |
1,3416 |
|
3 |
0,6 |
1,4850 |
0,0677 |
0,7 |
1,5527 |
0,1302 |
1,4832 |
|
4 |
0,8 |
1,6152 |
0,0625 |
0,9 |
1,6777 |
0,1210 |
1,6124 |
|
5 |
1,0 |
1,7362 |
|
|
|
|
1,7320 |
Абсолютная погрешность значения
![]() равна 0,0042, относительная погрешность
менее 0,3%.
равна 0,0042, относительная погрешность
менее 0,3%.
Для получения оценки погрешности часто
выполняют двойной пересчет: с шагом h
получают
![]() и с шагом
и с шагом
![]() получают
получают
![]() .
.
Если
![]() - точное значение решения в точке
- точное значение решения в точке
![]() ,
то погрешность для
,
то погрешность для
![]() оценивается при помощи равенства
оценивается при помощи равенства
![]() . (8)
. (8)
Метод Рунге–Кутта. Пусть дано дифференциальное уравнение (1) с начальными условиями (2).
Если
![]() ‑ приближенное значение решения
уравнения в точке
‑ приближенное значение решения
уравнения в точке
![]() ,
то значение
,
то значение
![]() в точке хi+1
=хi + h
будет равно:
в точке хi+1
=хi + h
будет равно:
![]() . (9)
. (9)
Для определения
![]() разложим функцию
разложим функцию
![]() в ряд Тейлора:
в ряд Тейлора:
![]()
Производные
![]() ,
... могут быть найдены последовательным
дифференцированием уравнения (1). Можно
показать, что с точностью до членов
четвертого порядка значение
,
... могут быть найдены последовательным
дифференцированием уравнения (1). Можно
показать, что с точностью до членов
четвертого порядка значение
![]() определится по формуле
определится по формуле
![]() , (10)
, (10)
где
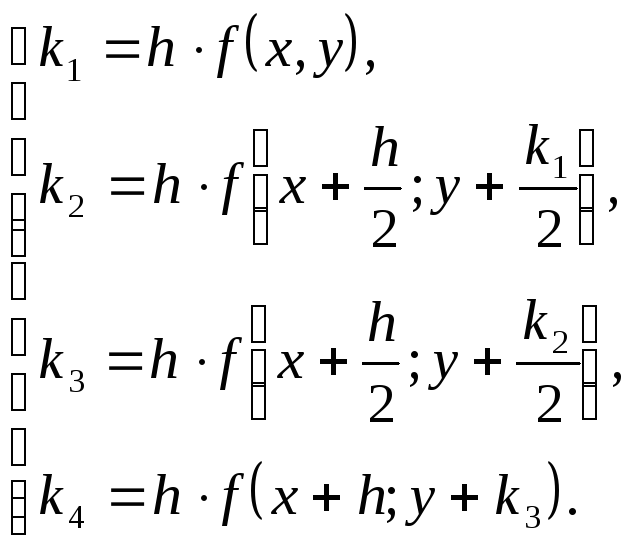 (11)
(11)
Таким образом, применение метода Рунге–Кутта сводится к последовательному вычислению значений:
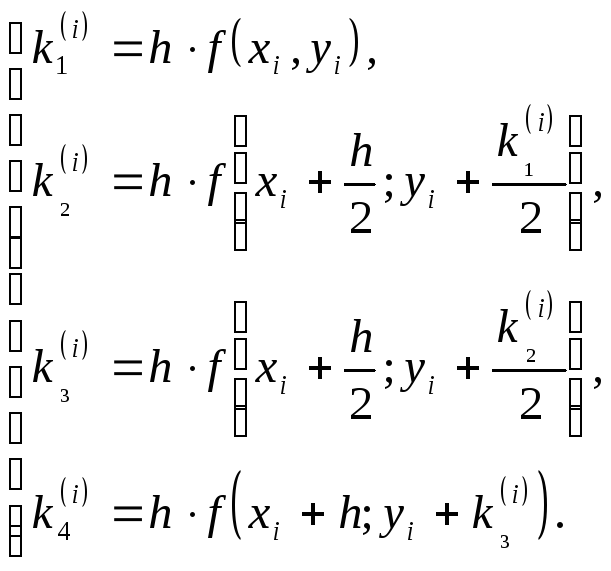 (12)
(12)
![]() (13)
(13)
и к нахождению значений по (9)
![]() .
.
Все вычисления удобно выполнять по определенной схеме (см. таблицу 3).
В первый раздел таблицы
![]() сначала записывают начальные значения
х0,
у0, а затем результаты
вычислений по формулам (12) и (13). Аналогично
заполняются и второй раздел таблицы
сначала записывают начальные значения
х0,
у0, а затем результаты
вычислений по формулам (12) и (13). Аналогично
заполняются и второй раздел таблицы
![]() ,
если считать, что начальной точкой
является точка
,
если считать, что начальной точкой
является точка
![]() .
.
Оценка погрешностей полученных значений
решения сложна. На практике обычно
пользуются двойным пересчетом при шаге
![]() и шаге
и шаге
![]() .
.
Абсолютная погрешность находится с помощью равенства
![]() , (14)
, (14)
где
![]() - значение точного решения в точке
- значение точного решения в точке
![]() и
и
![]() - приближенные значения, полученные
соответственно при шаге
- приближенные значения, полученные
соответственно при шаге
![]() и шаге
и шаге
![]() .
.
Если
![]() - заданная точность решения, то n
- число точек деления выбирается так,
чтобы шаг
- заданная точность решения, то n
- число точек деления выбирается так,
чтобы шаг
![]() удовлетворял условию
удовлетворял условию
![]() .
(15)
.
(15)
Пример. Пусть дано дифференциальное уравнение
![]()
с начальными условиями
![]() .
.
Найдем решение уравнения на отрезке
![]() с точностью до
с точностью до
![]() .
.
Выберем шаг, используя условие (15),
![]() .
.
Получим
![]() .
.
Возьмем
![]() и разобьем отрезок
и разобьем отрезок
![]() на шесть равных частей точками:
на шесть равных частей точками:
![]()
Найденные значения заносим в таблицу 4. Вычисления будем проводить с двумя запасными цифрами. Точным решением уравнения является функция
![]() .
.
Таблица C
|
i |
x |
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
0 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
1 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
... |
... |
... |
Таблица D
|
i |
x |
y |
|
|
|
|
|
0 |
1,5000 |
1,5000 |
0,3750 |
0,3750 |
|
|
0,125 |
1,6875 |
1,5625 |
0,3906 |
0,7812 |
|
0 |
0,125 |
1,6953 |
1,5703 |
0,3926 |
0,7852 |
|
|
0,25 |
1,8923 |
1,6426 |
0,4106 |
0,4106 |
|
|
|
|
|
|
0,3920 |
|
|
0,25 |
1,8920 |
1,6420 |
0,4105 |
0,4105 |
|
|
0,375 |
2,0973 |
1,7223 |
0,7306 |
0,7612 |
|
1 |
0,375 |
2,1073 |
1,7323 |
0,7331 |
0,7662 |
|
|
0,50 |
2,3251 |
1,8251 |
0,4562 |
0,4562 |
|
|
|
|
|
|
0,4323 |
|
|
0,50 |
2,3243 |
1,8243 |
0,4561 |
0,4561 |
|
|
0,625 |
2,5523 |
1,9283 |
04818 |
0,9626 |
|
2 |
0,625 |
2,5652 |
1,940 |
0,4850 |
0,9700 |
|
|
0,75 |
2,8093 |
2,0593 |
0,5148 |
0,5148 |
|
|
|
|
|
|
0,4841 |
|
|
0,75 |
2,8084 |
2,084 |
0,5146 |
0,5146 |
|
|
0875 |
3,0657 |
2,1908 |
0,5477 |
1,0854 |
|
3 |
0,875 |
3,0833 |
2,2073 |
0,5518 |
1,1036 |
|
|
1,00 |
3,3602 |
2,3602 |
05900 |
0,5900 |
|
|
|
|
|
|
0,5506 |
|
|
1,00 |
3,3590 |
2,3590 |
0,5898 |
0,5898 |
|
|
1,125 |
3,6529 |
2,5259 |
0,6322 |
1,2644 |
|
4 |
1,125 |
3,66751 |
2,5501 |
0,6375 |
1,2750 |
|
|
1,25 |
3,9965 |
2,7265 |
0,6866 |
0,6866 |
|
|
|
|
|
|
0,6360 |
|
|
1,25 |
3,9950 |
2,7450 |
0,6862 |
0,6862 |
|
|
1,375 |
3,3381 |
2,9561 |
0,7408 |
1,4816 |
|
5 |
1,375 |
4,3654 |
2,9904 |
0,7476 |
1,4952 |
|
|
1,50 |
4,7426 |
3,2426 |
0,8106 |
0,8106 |
|
|
|
|
|
|
0,7256 |
|
6 |
1,50 |
4,7406 |
|
|
|