Приближенное вычисление площадей плоских фигур

П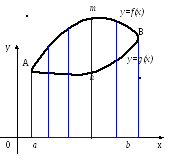усть плоская фигура Р ограничена замкнутым контуром С. Выберем систему координат таким образом, чтобы рассматриваемая фигура лежала в пером квадранте. Будем предполагать, что любая прямая, параллельная оси Оу, пересекает контур С не более, чем в двух точках. Спроецируем фигуру Р на ось Ох; в проекции получится отрезок [a; b].

Пусть А – точка фигуры с абсциссой х = а, В – точка фигуры с абсциссой х = b. Точки А и В разбивают контур С на две кривые верхнюю и нижнюю с уравнениями соответственно y = f(x) и y = g(x), где f(x), g(x) – непрерывные на отрезке [a; b] функции. Обозначим через Р площадь фигуры Р. Площадь Р будет равна разности площадей двух криволинейных трапеций:

аАтВb и aAhBb,

т.е. численно равна разности двух интегралов:

Приближенные значения этих интегралов могут быть вычислены по любой из квадратурных формул.

Разобьем отрезок [а; b] на n равных частей

[х₀ , х₁] , [х₁ , х₂], …,[ х_п-1; х_п]

(а=х₀ , х₁ , …, х_п=b).

Значения подынтегральной функции y= f(x) - g(x) будут вычисляться в узлах квадратурной формулы по соотношениям:

y_i= f(x_i) - g(x_i) (i = 0, 1, …,п).

Очевидно, что

y₀ = f(x₀) - g(x₀) = 0 и y_n= f(x_n) - g(x_n) = 0

Значения y_i – длины отрезков ординат в узловых точках, заключенных внутри фигуры Р. Если аналитические выражения функций f(x) и g(x) неизвестны, то y_i можно измерить, пользуясь чертежом.

Общие формулы Ньютона-Котеса

Пусть требуется вычислить определенный интеграл

I = ,

если на отрезке [а; b] функция задана таблицей с постоянным шагом h:

xi	x0	x1	x2	…	xn
yi	y0	y1	y2	…	yn

Подынтегральную функцию заменим первым интерполяционным многочленом Ньютона и получим:

f(x) = P_n(x) + R_n(x) (22)

где R_n(x) – остаточный член интерполирования. Интегрируя равенство (22), получим:

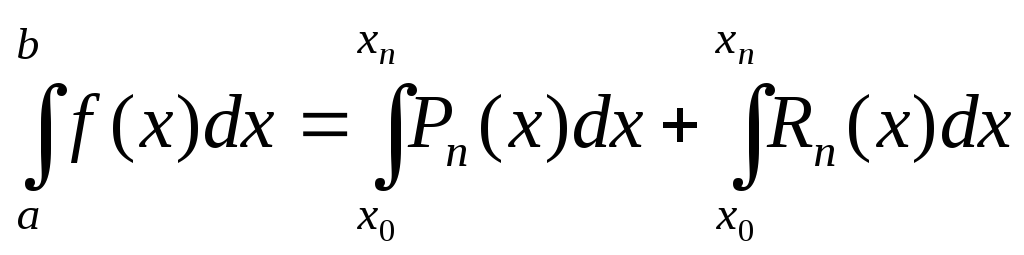
отбрасывая второе слагаемое в правой части, получим приближенное равенство

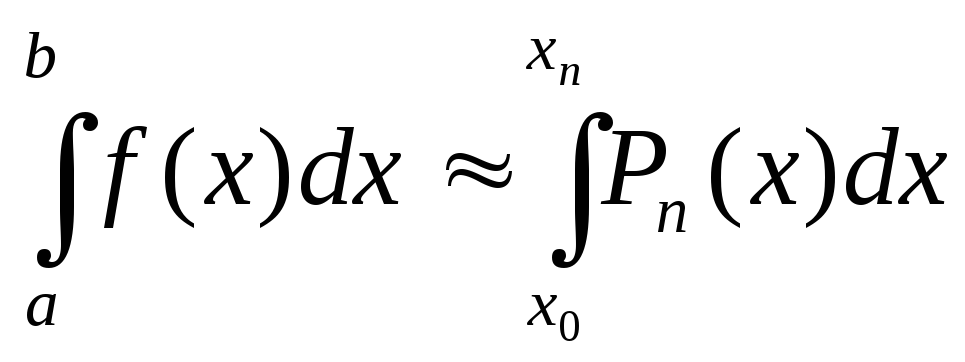, (23)

погрешность которого определяется формулой:

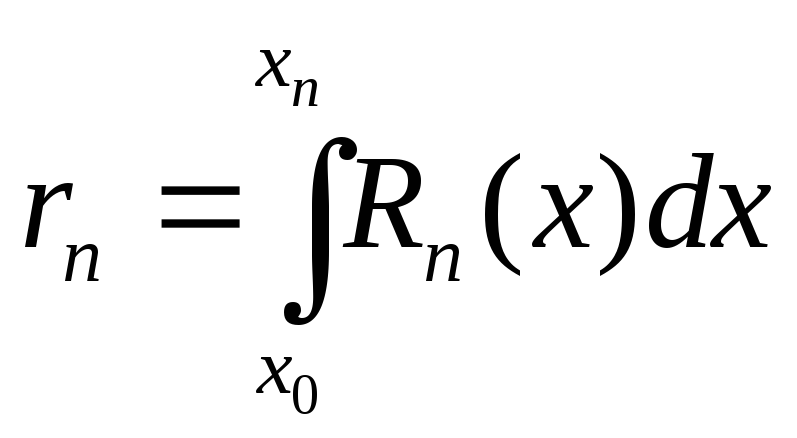. (24)

Равенство (23) называют квадратурными формулами Ньютона-Котеса. Из формулы (23) при п=1 получается формула трапеций, а при п=2 – формула Симпсона.

Вычисление интегралов простейшим методом Монте-Карло

Каким образом с помощью кучи камней измерить площадь пруда? Предположим, что пруд расположен в центре поля известной площади А. Бросайте камни в пруд произвольным образом так, чтобы они падали в случайных точках в пределах поля, и считайте количество всплесков при попадании камней в пруд. Эта простая процедура является примером метода Монте-Карло.

В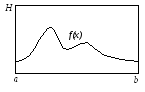ыясним подробнее суть этого метода. Пусть дан прямоугольник высотой Н и длиной b-a такой, что функция f(x) лежит внутри него. Генерируем п пар случайных чисел x_i и y_i, удовлетворяющих условиям a<= x_i <= b и 0 <= y_i <= H. Доля точек (x_i , y_i), которые удовлетворяют условию y_i<= f(x_i), представляет собой оценку отношения интеграла от функции f(x) к площади прямоугольника. Отсюда оценка F_n в методе "проб и ошибок" определяется выражением

, (4)

где n_s – число "всплесков" или точек, лежащих под кривой, п – общее количество точек, а А – площадь прямоугольника.

Другая разновидность метода Монте-Карло основывается на теореме математического анализа, согласно которой определенный интеграл

определяется средним значением подынтегральной функции f(x) на отрезке [a; b]. Для вычисления этого среднего возьмем x_i не с постоянным шагом, а случайным образом и произведем выборку значений f(x). Оценка F_n одномерного интеграла

методом "выборочного среднего" выражается формулой:

(5)

где x_i – случайные числа, равномерно распределенные на отрезке [a; b], а п – количество испытаний. Отличие формулы (5) от формулы прямоугольников только в том, что в рассматриваемом случае шаг не является постоянным. Для интегралов невысокой размерности формула прямоугольников оказывается точнее, чем формула (5), но для многомерных интегралов все же предпочтительнее формула (5).

Для реализации случайных чисел, равномерно распределенных на отрезке [a; b], можно использовать соотношение х=а+(b-a)r, где r –равномерно распределенные числа на отрезке [0; 1]. Для этого в программе требуется использование генератора случайных чисел. Например, х:=а+(b-a)random.