Алгоритмы C++
.pdf
Нахождение пары ближайших точек
Постановка задачи
Даны точек |
на плоскости, заданные своими координатами |
. Требуется найти среди них такие две |
точки, расстояние между которыми минимально: |
|
|
|
|
|
|
|
|
Расстояния мы берём обычные евклидовы:
|
|
|
Тривиальный алгоритм — перебор всех пар и вычисление расстояния для каждой — работает за |
. |
|
Ниже описывается алгоритм, работающий за время |
. Этот алгоритм был предложен Препаратой (Preparata) |
|
в 1975 г. Препарата и Шамос также показали, что в модели дерева решений этот алгоритм асимптотически оптимален.
Алгоритм
Построим алгоритм по общей схеме алгоритмов "разделяй-и-властвуй": алгоритм оформляем в виде рекурсивной функции, которой передаётся множество точек; эта рекурсивная функция разбивает это множество пополам, вызывает себя рекурсивно от каждой половины, а затем выполняет какие-то операции по объединению ответов. Операция объединения заключается в обнаружении случаев, когда одна точка оптимального решения попала в одну половину, а другая точка — в другую (в этом случае рекурсивные вызовы от каждой из половинок отдельно обнаружить эту пару, конечно, не смогут). Основная сложность, как всегда, заключается в
эффективной реализации этой стадии объединения. Если рекурсивной функции передаётся множество из 
точек,
то стадия объединения должна работать не более, чем |
, тогда асимптотика всего алгоритма |
будет находиться из уравнения: |
|
|
|
|
|
Решением этого уравнения, как известно, является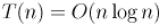 
.
Итак, перейдём к построению алгоритма. Чтобы в будущем прийти к эффективной реализации стадии объединения, разбивать множество точек на два будем согласно их 
-координатам: фактически мы проводим некоторую вертикальную прямую, разбивающую множество точек на два подмножества примерно одинаковых
размеров. Такое разбиение удобно произвести следующим образом: отсортируем точки стандартно как пары чисел, т.е.:
|
|
|
|
Тогда возьмём среднюю после сортировки точку |
( |
) и все точки до неё и саму |
отнесём к |
первой половине, а все точки после неё — ко второй половине:
|
|
|
|
|
Теперь, вызвавшись рекурсивно от каждого из множеств |
и |
, мы найдём ответы |
и |
для каждой из |
половинок. Возьмём лучший из них: |
. |
|
|
|
Теперь нам надо произвести стадию объединения, т.е. попытаться обнаружить такие пары точек, расстояние между которыми меньше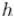 
, причём одна точка лежит в , а другая — в . Очевидно, что для этого
достаточно рассматривать только те точки, которые отстоят от вертикальной прямой раздела не расстояние, меньшее , т.е. множество 
рассматриваемых на этой стадии точек равно:
|
|
|
|
|
Для каждой точки из множества |
надо попытаться найти точки, находящиеся к ней ближе, чем |
. Например, |
||
достаточно рассматривать только те точки, координата которых отличается не более чем на |
. Более того, не |
|||
имеет смысла рассматривать те точки, у которых -координата больше |
-координаты текущей точки. Таким образом, |
|||
для каждой точки |
определим множество рассматриваемых точек |
следующим образом: |
||
|
|
|
|
|
|
|
|
|
|
Если мы отсортируем точки множества |
по -координате, то находить |
будет очень легко: это несколько |
точек подряд до точки . |
|
|
Итак, в новых обозначениях стадия объединения выглядит следующим образом: построить множество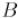 
, отсортировать в нём точки по 
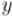-координате, затем для каждой точки 
рассмотреть все точки 
,
и каждой пары |
посчитать расстояние и сравнить с текущим наилучшим расстоянием. |
|
На первый взгляд, это по-прежнему неоптимальный алгоритм: кажется, что размеры множеств |
будут порядка , |
|
и требуемая асимптотика никак не получится. Однако, как это ни удивительно, можно доказать, что размер каждого из множеств есть величина , т.е. не превосходит некоторой малой константы вне зависимости от
самих точек. Доказательство этого факта приведено в следующем разделе.
Наконец, обратим внимание на сортировки, которых вышеописанный алгоритм содержит сразу две: сначала сортировка
по парам ( , ), а затем сортировка элементов множества |
по . На самом деле, от обеих этих сортировок |
|
внутри рекурсивной функции можно избавиться (иначе бы мы не достигли оценки |
для стадии объединения, и |
|
общая асимптотика алгоритма получилась бы |
). От первой сортировки избавиться легко — |
|
достаточно предварительно, до запуска рекурсии, выполнить эту сортировку: ведь внутри рекурсии сами элементы не меняются, поэтому нет никакой необходимости выполнять сортировку заново. Со второй сортировкой чуть сложнее, выполнить её предварительно не получится. Зато, вспомнив сортировку слиянием (merge sort), которая тоже работает по принципу разделяй-и-властвуй, можно просто встроить эту сортировку в нашу рекурсию.
Пусть рекурсия, принимая какое-то множество точек (как мы помним, упорядоченное по парам |
) возвращает это |
||||||||||
же множество, но отсортированное уже по координате . Для этого достаточно просто выполнить слияние (за |
) |
||||||||||
двух результатов, возвращённых рекурсивными вызовами. Тем самым получится отсортированное по |
множество. |
||||||||||
Оценка асимптотики |
|
|
|
|
|
|
|
|
|||
Чтобы показать, что вышеописанный алгоритм действительно выполняется за |
, нам осталось |
|
|||||||||
доказать следующий факт: |
|
. |
|
|
|
|
|
|
|
||
Итак, пусть мы рассматриваем какую-то точку |
; напомним, что множество |
— это множество точек, |
- |
||||||||
координата которых не больше |
, но и не меньше |
, а, кроме того, по координате и сама точка , и все |
|||||||||
точки множества |
лежат в полосе шириной |
. Иными словами, рассматриваемые нами точки |
и |
лежат |
|||||||
в прямоугольнике размера |
. |
|
|
|
|
|
|
|
|
||
Наша задача — оценить максимальное количество точек, которое может лежать в этом прямоугольнике |
; |
||||||||||
тем самым мы оценим и максимальный размер множества |
|
(он будет на единицу меньше, т.к. в |
|
||||||||
этом прямоугольнике лежит ещё и точка ). При этом надо не забывать, что в общем случае могут встречаться |
|||||||||||
и повторяющиеся точки. |
|
|
|
|
|
|
|
|
|
||
Вспомним, что |
получалось как минимум из двух результатов рекурсивных вызовов — от множеств |
и |
, |
||||||||
причём |
содержит точки слева от линии раздела и частично на ней, |
— оставшиеся точки линии раздела и |
|||||||||
точки справа от неё. Для любой пары точек из |
|
, равно как и из |
, расстояние не может оказаться меньше |
— |
|||||||
иначе бы это означало некорректность работы рекурсивной функции. |
|
|
|
|
Для оценки максимального количества точек в прямоугольнике |
разобьём его на два квадрата |
, к |
||
первому квадрату отнесём все точки |
, а ко второму — все остальные, т.е. |
. Из |
|
|
приведённых выше соображений следует, что в каждом из этих квадратов расстояние между любыми двумя точками не превосходит 
. Но тогда это означает, что в каждом квадрате не более четырёх точек!
Действительно, пусть есть квадрат |
, и расстояние между любыми двумя точками не превосходит той же |
|||
. Докажем, что в квадрате не может быть больше 4 точек. Например, это можно сделать следующим образом: |
||||
разобьём этот квадрат на 4 квадрата со сторонами |
. Тогда в каждом из этих маленьких квадратов не может |
|||
быть больше одной точки (т.к. даже диагональ равна |
, что меньше |
). Следовательно, во всём квадрате никак |
||
не может быть более 4 точек. |
|
|
|
|
Итак, мы доказали, что в прямоугольнике |
не может быть больше |
точек, а, следовательно, |
||
размер множества |
не может превосходить 7, что и требовалось доказать. |
|||
Реализация
Введём структуру данных для хранения точки (её координаты и некий номер) и операторы сравнения, необходимые для двух видов сортировки:
struct pt {
int x, y, id;
};
inline bool cmp_x (const pt & a, const pt & b) { return a.x < b.x || a.x == b.x && a.y < b.y;
}
inline bool cmp_y (const pt & a, const pt & b) { return a.y < b.y;
}
pt a[MAXN];
Для удобной реализации рекурсии введём вспомогательную функцию |
, которая будет вычислять |
расстояние между двумя точками и проверять, не лучше ли это текущего ответа: |
|
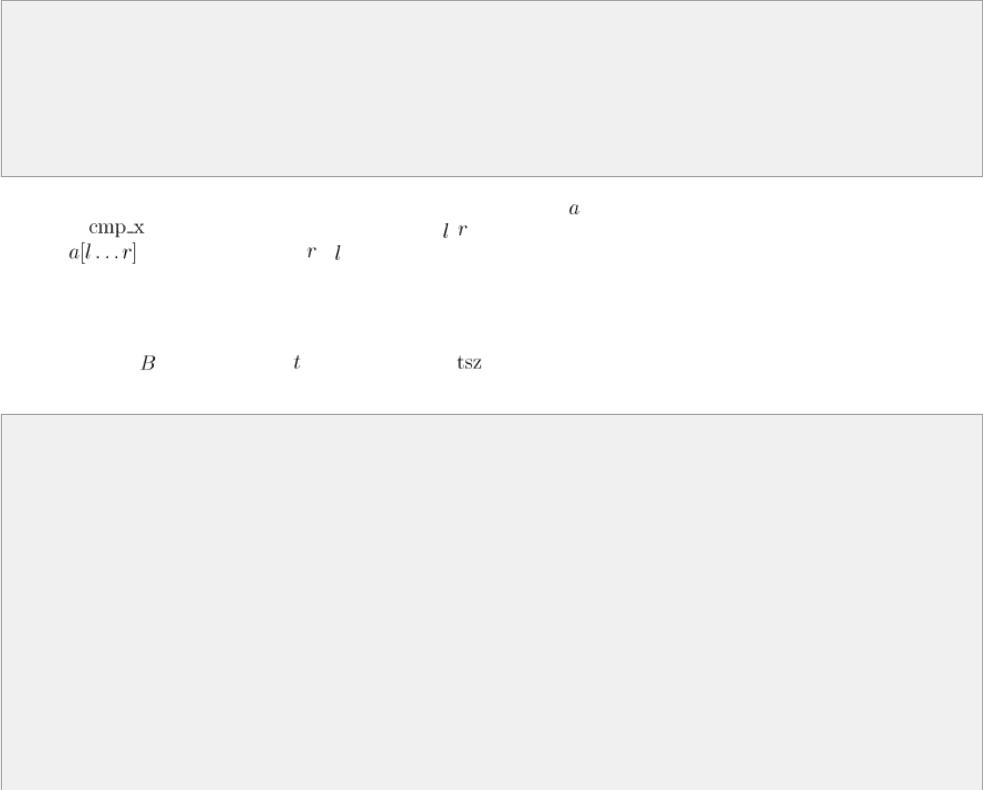
double mindist; int ansa, ansb;
inline void upd_ans (const pt & a, const pt & b) {
double dist = sqrt ((a.x-b.x)*(a.x-b.x) + (a.y-b.y)*(a.y-b.y) + .0); if (dist < mindist)
mindist = dist, ansa = a.id, ansb = b.id;
}
Наконец, реализация самой рекурсии. Предполагается, что перед её |
вызовом массив уже отсортирован по |
|
компаратору |
. Рекурсии передаётся просто два указателя , |
, которые указывают, что она должна искать |
ответ для |
. Если расстояние между и слишком мало, то рекурсию надо остановить, и |
|
выполнить тривиальный алгоритм поиска ближайшей пары и затем отсортировать подмассив по компаратору 
.
Внутри рекурсии для выполнения слияния по компаратору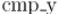 
используется стандартная функция
STL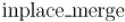 
.
Наконец, множество хранится в массиве , длина которого равна . Этот массив статический, т.е. общий для всех уровней рекурсии, а не выделяется заново при каждом вызове (примерно то же самое, что сделать его глобальным).
void rec (int l, int r) { if (r - l <= 3) {
for (int i=l; i<=r; ++i)
for (int j=i+1; j<=r; ++j) upd_ans (a[i], a[j]);
sort (a+l, a+r+1, &cmp_y); return;
}
int m = (l + r) >> 1; int midx = a[m].x;
rec (l, m), rec (m+1, r);
inplace_merge (a+l, a+m+1, a+r+1, &cmp_y);
static pt t[MAXN]; int tsz = 0;
for (int i=l; i<=r; ++i)
if (abs (a[i].x - midx) < mindist) {
for (int j=tsz-1; j>=0 && a[i].y - t[j].y < mindist; --j) upd_ans (a[i], t[j]);
t[tsz++] = a[i];
}
}
Кстати говоря, если все координаты целые, то на время работы рекурсии можно вообще не переходить к дробным величинам, и хранить в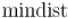 
квадрат минимального расстояния.
Восновной программе вызывать рекурсию следует так:
sort (a, a+n, &cmp_x); mindist = 1E20;
rec (0, n-1);
Преобразование геометрической инверсии
Преобразование геометрической инверсии (inversive geometry) — это особый тип преобразования точек на плоскости. Практическая польза этого преобразования в том, что зачастую оно позволяет свести решение геометрической задачи с окружностями к решению соответствующей задачи с прямыми, которая обычно имеет гораздо более простое решение.
По всей видимости, основоположником этого направления математики был Людвиг Иммануэль Магнус (Ludwig Immanuel Magnus), который в 1831 г. опубликовал статью об инверсных преобразованиях.
Определение
Зафиксируем окружность с центром в точке радиуса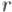 
. Тогда инверсией точки относительно этой окружности называется такая точка 
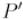, которая лежит на луче 
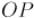, а на расстояние наложено условие:
|
|
|
Если считать, что центр |
окружности совпадает с началом координат, то можно сказать, что точка |
имеет тот |
же полярный угол, что и , а расстояние вычисляется по указанной выше формуле. |
|
|
В терминах комплексных чисел преобразование инверсии выражается достаточно просто, если считать, что центр 
окружности совпадает с началом координат:
С помощью сопряжённого элемента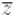 
можно получить более простую форму:
Применение инверсии (в точке-середине доски) к изображению шахматной доски даёт интересную картинку (справа):
Свойства
Очевидно, что любая точка, лежащая на окружности, относительно которой производится преобразование инверсии, при отображении переходит в себя же. Любая точка, лежащая внутри окружности, переходит во внешнюю область, и наоборот. Считается, что центр окружности переходит в точку "бесконечность"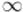 
, а точка "бесконечность" — наоборот, в центр окружности:
Очевидно, что повторное применение преобразования инверсии обращает первое её применение — все точки возвращаются обратно:
Обобщённые окружности
Обобщённая окружность — это либо окружность, либо прямая (считается, что это тоже окружность, но имеющая бесконечный радиус).
Ключевое свойство преобразования инверсии — что при его применении обобщённая окружность всегда переходит в обобщённую окружность (подразумевается, что преобразование инверсии поточечно применяется ко всем точкам фигуры).
Сейчас мы увидим, что именно происходит с прямыми и окружностями при преобразовании инверсии.
Инверсия прямой, проходящей через точку 
Утверждается, что любая прямая, проходящая через |
, после преобразования инверсии не меняется. |
|||
В самом деле, любая точка этой прямой, кроме |
и |
, переходит по определению тоже в точку этой прямой (причём |
||
в итоге получившиеся точки заполнят всю прямую целиком, поскольку преобразование инверсии обратимо). |
||||
Остаются точки |
и |
, но при инверсии они переходят друг в друга, поэтому доказательство завершено. |
||
Инверсия прямой, не проходящей через точку 
Утверждается, что любая такая прямая перейдёт в окружность, проходящую через 
.
Рассмотрим любую точку |
этой прямой, и рассмотрим также точку |
— ближайшую к |
точку прямой. Понятно, |
что отрезок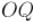 
перпендикулярен прямой, а потому образуемый им угол 
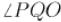— прямой.
Воспользуемся теперь леммой о равных углах, которую мы докажем чуть позже, эта лемма даёт нам равенство: