Алгоритмы C++

memset (st[0].next, -1, sizeof st[0].next); ++sz;

}

void sa_extend (char c) { int nlast = sz++;

st[nlast].length = st[last].length + 1;

memset (st[nlast].next, -1, sizeof st[nlast].next); int p;

for (p=last; p!=-1 && st[p].next[c]==-1; p=st[p].link) st[p].next[c] = nlast;

if (p == -1)

st[nlast].link = 0;

else {

int q = st[p].next[c];

if (st[p].length + 1 == st[q].length) st[nlast].link = q;

else {

int clone = sz++;

st[clone].length = st[p].length + 1;

memcpy (st[clone].next, st[q].next, sizeof st

[clone].next);

st[clone].link = st[q].link;

for (; p!=-1 && st[p].next[c]==q; p=st[p].link) st[p].next[c] = clone;

st[q].link = st[nlast].link = clone;

}

}

last = nlast;

}

void mark_terminal() {

for (int p=last; p!=-1; p=st[p].link) st[p].terminal = true;

}

Чтобы уменьшить потребление памяти до O (N), но ценой увеличения времени работы до O (N log K), достаточно небольших изменений в этом коде. Массив int next[K] надо заменить на map<char,int> next,

и соответствующим образом изменить весь код: убрать memset'ы, выражение st[p].next[c]==-1 заменить на !st[p].next. count(c), а выражение st[p].next[c]==q заменить на st[p].next.count(c) && st[p].next[c]==q.

Применения

Пусть дана строка S, для которой построен суффиксный автомат за ту или иную асимптотику.

Тогда мы можем решить следующие задачи (в их асимптотики построение автомата, конечно, не включено):

●Дана строка P, требуется за O(|P|) проверить, входит ли она в текст S.

Это сделать очень легко: стартуем из начального состояния Init, и пройдём по строке P, выполняя

соответствующие переходы по автомату. Если в какой-то момент мы не смогли сделать переход (по той причине, что его не существовало), то строка P в текст не входит; иначе же P содержится в S.

●Дана строка P, требуется за O(|P|) вывести позицию её первого вхождения в текст S.

Чтобы решить эту задачу, понадобится добавить ещё одно информационное поле в суффиксный автомат: endpos. Для каждого состояния p endpos[p] будет равно позиции, в которой оканчиваются первые вхождения всех

строк, соответствующих p. Здесь имеется в виду, что одному состоянию может соответствовать несколько строк, однако, можно доказать, что среди них найдётся одна такая, что все остальные будут её суффиксами. Тогда ясно, почему для каждого состояния мы не можем посчитать позицию начала первого вхождения - её просто невозможно определить, она будет различной для разных строк. А вот позицию окончания мы можем определить (как раз на основе того, что все строки являются суффиксами одной строки).

Теперь, как же вычислять endpos при построении автомата? Для добавляемого состояния nlast endpos будет равен длине текущей строки - т.е. endpos[nlast] = length[nlast] - 1 (если в 0-индексации). При расщеплении для clone значение endpos будет равно endpos[q] (опять же, оправдывая название "clone").

Теперь вернёмся к нашей задаче. Снова, как и в предыдущей задаче, стартуем из состояния Init, выполним все переходы, придя к какому-то состоянию p. Тогда ответом будет endpos[p] - P.length() + 1.

●Дана строка P, требуется за O(|P| + AnsSize) вывести позиции всех вхождений в текст S.

Посчитаем величины endpos, как описано в предыдущей задаче, также добавим специальный флаг clonned[p], который будет равен true для состояний, полученных расщеплением (т.е. для clone), и false для остальных. Пусть

мы выполнили все переходы по строке P, пришли в некоторое состояние p. Первое вхождение в текст S оканчивается

в позиции endpos[p]. Как нам найти список состояний, для которых endpos будет также указывать на конец

некоторого вхождения? Если немного подумать, то понятно, что для этого достаточно запустить обход в ширину/глубину по инвертированным суффиксным ссылкам link. Действительно, если на некоторое состояние p указывают суффиксные ссылки из других состояний q1, q2, ..., то строка, соответствующая p, является суффиксом

строк, соответствующих им; это и означает то, что endpos[q1], endpos[q2], ... дадут нам позиции окончания вхождений, равно как и endpos[p]. Пустив обход в ширину/глубину по инвертированным суффиксным ссылкам, мы найдём все позиции, в которых оканчиваются вхождения (так как циклов в графе из суффиксных ссылок нет, то для обхода в ширину/глубину даже не понадобится массив used). Однако при таком способе в выводе появятся повторы; но нетрудно заметить, что все повторы вызваны только лишь clonned-вершинами. Действительно, с одной стороны,

если не добавлять endpos от clonned-вершин в ответ, то повторы никак не могут возникнуть - величины endpos различны для всех оставшихся вершин. С другой стороны, заметим, что при расщеплении выполняется: link[q] = clone, т. е. при обходе в ширину из вершины clone мы рано или поздно дойдём до q, и выведем её endpos. Следовательно,

мы ничего не потеряем в ответе, если просто не будет выводить endpos для clonned-вершин.

Осталось только понять, что асимптотика этого обхода действительно будет O(AnsSize). Но это очевидный факт, поскольку не-clonned-вершины добавляют в ответ по одному числу, а из каждой clonned-вершины достижима хотя бы одна не-clonned.

Наконец, число реализационный момент - что здесь для экономии памяти вместо введения флага clonned можно просто присваивать endpos[clone] = -1.

Для большей ясности приведём здесь часть кода:

выполняющую построение графа инвертированных суффиксных ссылок:

struct state {

int length, link, endpos; map<char,int> next; vector<int> ilink;

};

int main() {

... построение автомата ...

for (int i=1; i<sz; ++i) st[st[i].link].ilink.push_back (i);

...

}

ивыполняющую вывод ответа:

void dfs (int p, int len) {

if (st[p].endpos != -1)

printf ("%d ", st[p].endpos-len+2); // при выводе делаем

1-индексацию

for (size_t i=0; i<st[p].ilink.size(); ++i) dfs (st[p].ilink[i], len);

}

int main() {

...

dfs (p, (int)P.length()); // p - текущее состояния, P -

искомая подстрока

...

}

Осталось только заметить, что выводиться позиции будут в неизвестно каком порядке, совсем необязательно, что отсортированными.

●Дана строка P, требуется найти за O (|P|) количество вхождений её в текст S.

Посчитаем для каждого состояния такую динамику: cnt[p] - количество вхождений строк, которым соответствует состояние p. Тогда ответом к задаче будет просто величина cnt[p], где p - состояние, соответствующее строке

P.Проинициализируем cnt[p] = 1, если p - не-clonned-вершина, и 0 - если clonned. Потом посчитаем динамику таким образом: cnt[link[p]] += cnt[p]. Разумеется, вычислять её нужно в таком порядке, чтобы к этому моменту cnt[p]

уже было вычислено. Например, это можно сделать, отсортировав состояния по длине length в порядке уменьшения.

●По данной строке S найти за O (|S|) наикратчайшую подстроку, не входящую в S в качестве подстроки. Это решается динамикой по автомату. Пусть d[p] - это ответ для состояния p - длина кратчайшей подстроки. Если из p нет перехода хотя бы по одной букве, то d[p] = 1 (мы берём эту букву; короче, очевидно, строки найтись не может), иначе же мы одной буквой обойтись не может, и тогда d[p] будет равно минимуму из 1 + d[st[p].next[c]] для всех c (т.е.

мы добавляем одну букву и берём ответ для этого состояния). Восстановить саму строку - ответ, - также будет несложно.

●Найти наименьший циклический сдвиг строки S за O(|S|).

Здесь построим автомат не для строки S, а для строки S+S. Тогда наша задача сводится к нахождению пути длины

N(имеется в виду N рёбер) с наименьшей меткой (метка пути - строка, соответствующая ему). Но это

абсолютно элементарная задача - начнём из состояния Init и будет идти, на каждом шаге жадно выполняя переход

с наименьшей буквой (нетрудно понять, почему мы никогда не упрёмся в "тупик", из которого нет ни одного перехода).

●Количество различных подстрок за O(|S|).

Эту задачу решим динамикой по состояниям автомата. Пусть d[p] - ответ для состояния p, тогда d[p] = Сумме (d[q] + 1) по всем переходам из p в состояния q. Действительно, мы как бы фиксируем первый символ подстроки, берём ответ для нового состояния, и затем прибавляем к нему единицу - это под строка длины 1, состоящая только из этого фиксированного символа.

●Суммарная длина всех различных подстрок за O(|S|).

Эта задача очень похожа на предыдущую, и здесь нам также понадобится та же динамика d[p] - количество различных подстрок. Сам же ответ SumLen будет считаться как SumLen[p] = СУММА (d[q] + SumLen[q] + 1) - мы как бы дописываем первый символ к каждой из строк, учтённых в SumLen[q].

●Дана строка T, и требуется найти все вхождения в неё строки S за O (|T|) при том, что автомат по-прежнему построен для строки S (это обратная постановка задачи поиска строк).

Стартуем из состояния Start, и пусть p - это текущее состояние, а l - текущая длина совпадающего куска (изначально она, очевидно, равна нулю), и будем по очереди перебирать символы строки T; пусть текущий символ - символ С. Если

из текущего состояния p есть переход по символу C, то просто совершаем этот переход, и увеличиваем l на единицу; если l стало равно длине строки S, то мы нашли вхождение - оно как раз оканчивается в текущей позиции в строке T. Если же

из текущего состояния p перехода нет, то это означает, что совпадающий кусок мы никак не сможем увеличить; значит, нам надо пытаться найти наибольший суффикс совпадающего куска такой, что к нему можно дописать символ C. Вспоминая понятие суффиксной ссылки, это можно сформулировать так: будем двигаться по суффиксному

пути состояния p, пока не встретим состояние, из которого есть переход по символу C. Если мы найдём такое состояние, то надо установить значение l: l = length[p] + 1 (поскольку символ C дописываем). Если же такого состояния мы так и не найдём, то l = 0, p = Init - т.е. совпадающая часть вообще пуста.

Нетрудно понять, почему этот код работает за O (|T|) - мы на каждом шаге либо увеличиваем длину совпадающей части на единицу, либо же уменьшаем на сколько-либо (на неотрицательную величину).

Для большей ясности приведём фрагмент реализации (в предположении, что next задано массивом, но сути это никак не меняет):

int l = 0, p = 0;

for (size_t i=0; i<t.length(); ++i) { char c = t[i];

if (st[p].next[c] != -1)

++l, p = st[p].next[c];

else {

for (; p!=-1 && st[p].next[c]==-1; p=st[p].link) ; if (p == -1)

l = 0, p = 0;

else

l = st[p].length + 1, p = st[p].next[c];

}

if (l == (int)s.length()) cout << i-l+1 << ' ';

}

Кстати говоря, можно ещё ускорить этот алгоритм (уменьшить скрытую константу), если предпосчитать заранее результат выполнения цикла for. Действительно, результат этого цикла зависит только от текущего состояния p и текущего символа C, и результат выполнения этого цикла (так называемые "оптимизированные суффиксные ссылки")

- новое значение p - можно предпосчитать за O (|S| K).

●Даны строки S и T, требуется найти их наидлиннейшую общую подстроку (LCS) за O(|S|+|T|). Построим по строке S суффиксный автомат. Теперь будем идти по строке T и для каждой позиции в ней находить длину наидлиннейшего суффикса, оканчивающегося в этой позиции и встречающегося в S. Ясно, что

искомая наидлиннейшая общая подстрока будет оканчиваться в той позиции, в которой эта величина максимальна. Будем поддерживать переменную p - текущее состояние в автомате, и l - текущая длина наидлиннейшего суффикса. Изначально p = Init, l = 0. Пусть мы нашли эти значения для T[i-1], покажем, как найти их для T[i]. Если

из состояния p суффиксного автомата (для строки S) есть переход по букве T[i], то просто выполняем этот переход (т.е. p

= st[p].next[T[i]]) и увеличиваем длину суффикса на единицу (++l). Если же из состояния p такого перехода нет, то мы вынуждены попытаться укоротить текущий суффикс, т.е. перейти по его суффиксной ссылке (т.е. p = st[p].link) и выбрать в качестве текущего суффикса длиннейшую строку, соответствующую этом состоянию (т.е. l = st[p]. length); причём это мы должны повторять до тех пор, пока не найдём состояние p с имеющимся переходом по T[i] (тогда мы приходим к предыдущему пункту - т.е. выполняем переход и увеличиваем l), или пока у нас не кончатся состояния (т.е. p не станет равно -1).

После построения автомата за O(|S|) выполняется только O(|T|) действий, поскольку величина l неотрицательна, и при обработке каждого символа может увеличиться максимум на единицу (а при переходе по суффиксной ссылке она строго уменьшается).

Итого имеем такой код:

string lcs (string a, string b) { init();

for (size_t i=0; i<a.length(); ++i) sa_extend (a[i]);

int p = 0, l = 0, best = 0, bestpos = 0; for (size_t i=0; i<b.length(); ++i) {

if (st[p].next[b[i]-'A'] == -1) {

for (; p!=-1 && st[p].next[b[i]-'A'] == -1; p=st

[p].link) ;

if (p == -1) {

p = l = 0; continue;

}

l = st[p].length;

}

p = st[p].next[b[i]-'A']; ++l;

if (l > best)

best = l, bestpos = (int)i;

}

return b.substr (bestpos-best+1, best);

}

Нахождение всех подпалиндромов

Постановка задачи

Дана строка длины . Требуется найти все такие пары

, где

, что подстрока

является палиндромом (т.е. читается одинаково слева направо и справа налево).

Понятно, что в худшем случае таких подстрок-палиндромов может быть		, однако информацию можно
возвращать более компактно: для каждой позиции	найдём значения		и	,

обозначающие количество палиндромов соответственно нечётной и чётной длины с центром в позиции . Например, для строки значение :

А для строки значение :

Идея в том, что если есть подпалиндром длины с центром в какой-то позиции			, то есть также подпалиндромы
длины	,	, и т.д. с центрами в , поэтому двух таких массивов	и	достаточно для

хранения информации обо всех подпалиндромах этой строки.

Более удивительным является то, что существует довольно простой алгоритм, который вычисляет эти массивы за линейное время, этот алгоритм и описывается ниже.

Алгоритм решения

Эта задача имеет несколько известных решений: с помощью хэширования её можно решить за , а с

помощью суффиксных деревьев и быстрого алгоритма LCA эту задачу можно решить за .

Однако описаный ниже метод значительно проще, и обладает меньшими скрытыми константами в асимптотике времени и памяти. Этот алгоритм был открыт Гленном Манакером (Glenn Manacher) в 1975 г.

Научимся сначала находить все подпалиндромы нечётной длины, т.е. вычислять массив							; решение для
палиндромов чётной длины получится небольшой модификацией этого.
Для быстрого вычисления будем поддерживать границы				самого правого обнаруженного подпалиндрома (т.е.
с наибольшим значением ). Изначально можно положить				.
Итак, пусть мы хотим вычислить значение			для очередного , при этом все предыдущие значения
уже подсчитаны. Если не находится в пределах текущего подпалиндрома, т.е.						, то выполним
тривиальный алгоритм (т.е. будем последовательно увеличивать значение					, пока не найдём
границу подпалиндрома); после этого мы должны не забыть обновить значения						.
Рассмотрим теперь случай, когда		. Попробуем извлечь часть информации из уже подсчитанных значений						,
а именно, отразим позицию	внутри подпалиндрома			, т.е. получим позицию			, и
рассмотрим значение	. Поскольку		— позиция, симметричная позиции		, то мы можем взять ответ			в

качестве ответа , но за одним исключением. Иллюстрация этого отражения в простом случае (палиндром вокруг фактически "копируется" в палиндром вокруг ):

Особым случаем является случай, когда "внутренний палиндром" достигает границы внешнего или вылазит за неё, т.

е.	. Поскольку за границами внешнего палиндрома никакой симметрии нет, то при
переносе подпалиндрома из позиции в позицию его нужно "обрезать", т.е. присвоить		. После
этого следует пустить тривиальный алгоритм, который будет пытаться увеличить значение		(он уже будет

выходить за пределы "внешнего" палиндрома). Иллюстрация этого случая (на ней палиндром с центром в уже "обрезан" до такой длины, что он впритык помещается во внешний):

Итак, мы описали поведение алгоритма в двух принципиально разных ситуациях. Осталось только заметить, что надо не забывать обновлять значения 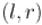после вычисления очередного значения .

Оценка асимптотики

Заметим, что на каждой, -ой, стадии алгоритма сначала выполняются некоторые вычисления за

, а

затем запускается процесс тривиального обнаружения подпалиндромов большей длины. Более того, каждая итерация этого тривиального цикла (кроме последней) приводит в дальнейшем к продвижению указателя вправо.

Влево этот указатель у нас тоже никогда не двигается. Поскольку этот указатель не мог выйти за пределы всей строки, т. е. , то мы получаем, что суммарно произойдёт не более успешных итераций тривиального алгоритма. Т.к.

все остальные части алгоритма работают также за , мы получаем итоговую асимптотику алгоритма: .

Реализация

Для случая палиндромов нечётной длины, т.е. для вычисления получаем такой код:

vector<int> d1 (n); int l=0, r=-1;

for (int i=0; i<n; ++i) {

int k = (i>r ? 0 : min (d1[l+r-i], r-i)) + 1;

while (i+k < n && i-k >= 0 && s[i+k] == s[i-k]) ++k; d1[i] = --k;

if (i+k > r)

l = i-k, r = i+k;

}

Для подпалиндромов чётной длины рассуждения те же самые, просто немного поменяются арифметические выражения:

vector<int> d2 (n); l=0, r=-1;

for (int i=0; i<n; ++i) {

int k = (i>r ? 0 : min (d2[l+r-i+1], r-i+1)) + 1;

while (i+k-1 < n && i-k >= 0 && s[i+k-1] == s[i-k]) ++k; d2[i] = --k;

if (i+k-1 > r)

l = i-k, r = i+k-1;

}