Алгоритмы C++

Нахождение треугольника наименьшей площади за O (N2 log N)

Пусть даны N точек на плоскости. Требуется найти невырожденный треугольник наименьшей площади, вершины которого находятся в этих точках.

Алгоритм будет следующим. Последовательно переберём все точки, и для каждой точки Pi выполним следующие действия.

Рассмотрим все остальные точки, и для каждой точки будем рассматривать только её относительные

координаты (относительно P[i]). Очевидно, что в этом случае площадь треугольника Pi Pj Pk будет равна 0.5 * |X1 * Y2 - X2 * Y1|, где X1, Y1, X2, Y2 - координаты точек Pj и P соответственно (см. "ориентированная площадь

треугольника"). Следовательно, тот треугольник будет обладать наименьшей площадью, у которого модуль разности X1 * Y2 - X2 * Y1 будет наименьшим.

Если мы будем тривиально перебирать всевозможные пары вершин j и k, то общая асимптотика решения достигнет O

(N3), что нас не устраивает. Однако можно пойти другим путём: зафиксировав некоторое i, отсортировать все остальные вершины, используя для сравнения предикат X1 * Y2 < X2 * Y1. Теперь, если мы пройдёмся

по отсортированному таким образом массиву вершин и рассмотрим каждую пару соседних вершин, то среди них

мы обязательно рассмотрим треугольник минимальной площади. Теперь, очевидно, асимптотика решения составит O (N2 log N).

Реализация

struct point { double x, y;

};

bool my_cmp (point p1, point p2)

{

return p1.x * p2.y < p2.x * p1.y;

}

const double EPS = 1E-8; const double INF = 1E+20;

int main()

{

int n; vector<point> a;

... чтение ...

double result = INF; for (int i=0; i<n; i++)

{

vector<point> b (a); for (int j=0; j<n; j++)

b[j].x -= a[i].x, b[j].y -= a[i].y; sort (b.begin(), b.end(), my_cmp);

for (int j=1; j<n; j++)

{

double s = 0.5 * (b[j].x * b[j-1].y - b[j].y * b[j-

1].x);

if (s > EPS)

result = min (result, s);

}

}

cout << result;

}

Z-фунция строки и её вычисление за O (N)

Z-функция ("зет-функция") от строки S - это массив Z, каждый элемент которого Z[i] равен наидлиннейшему

префиксу подстроки, начинающейся с позиции i в строке S, который одновременно является и префиксом всей строки S. Значение Z-функции в позиции 0 обычно считается не определенным (или, например, равным нулю).

Задача - посчитать Z-функцию для некоторой строки длины N за время O (N).

Алгоритм

Смысл алгоритма заключается в том, чтобы при вычислении текущего значения Z-функции стараться максимально использовать уже вычисленные значения. Для этого мы будем хранить переменные-индексы L и R,

которые будут указывать на начало и конец текущего префикса. Теперь, если текущая позиция I находится между L и R включительно, то мы постараемся использовать предыдущие значения. Поскольку мы находимся внутри подстроки, являющейся префиксом всей строки, то мы можем посмотреть значение Z-функции в начале строки в

позиции J, соответствующей текущей позиции I, т.е. J = I - L. Если значение Z[J] "помещается" внутрь текущего префикса, т.е. Z[J] < R - I + 1, то выполняется Z[I] = Z[J]. Если же "не помещается", то придётся выполнить дополнительную

работу: пройтись по символам, стоящим после окончания текущего префикса и найти последнее совпадение; теперь нам известно значение Z-функции, а также мы можем подправить значения L и R, увеличив их. Последний оставшийся случай - когда I находится вне текущего префикса, т.е. I > R, решается тривиальным циклом.

Реализация

void calc_z (const char * s, vector<unsigned> & z)

{

unsigned len = strlen (s); z.resize (len);

z[0] = 0;

unsigned l = 0,	r = 0;
for (unsigned i	= 1; i < len; i++)
if (i >	r)
{

unsigned j;

for (j = 0; i+j < len && s[i+j] == s[j]; j++) ; z[i] = j;

l = i;

r = i + j - 1;

}

else

if (z[i-l] < r - i + 1) z[i] = z[i-l];

else

{

unsigned j;

for (j = 1; r+j < len && s[r+j] == s[r-i+j]; j

++) ;

z[i] = r - i + j; l = i;

r = r + j - 1;

}

}

Можно значительно уменьшить размер кода, правда, в ущерб понятности:

void calc_z (const char * s, vector<int> & z)

{

int len = (int) strlen (s); z.resize (len);

int l = 0, r = 0;

for (int i=1; i<len; ++i) if (z[i-l]+i <= r)

z[i] = z[i-l];

else

{

l = i;

if (i > r) r = i;

for (z[i] = r-i; r<len; ++r, ++z[i]) if (s[r] != s[z[i]])

break;

--r;

}

}

Префикс-функция. Алгоритм Кнута-Морриса-Пратта

Префикс-функция. Определение

Дана строка		. Требуется вычислить для неё префикс-функцию, т.е. массив чисел	,
где	определяется следующим образом: это длина наибольшего собственного суффикса подстроки
	, совпадающего с её префиксом (собственный суффикс — значит не совпадающий со всей строкой). В

частности, значение всегда равно нулю.

Математически определение префикс-функции можно записать следующим образом:

Например, для строки "abcabcd" префикс-функция равна:		. Для строки "aabaaab" она
равна:	.

Тривиальный алгоритм

Непосредственно следуя определению, можно написать такой алгоритм вычисления префикс-функции (как нетрудно заметить, работать он будет за ):

vector<int> prefix_function (string s) { int n = (int) s.length(); vector<int> pi (n);

for (int i=0; i<n; ++i)

for (int k=0; k<=i; ++k)

if (s.substr(0,k) == s.substr(i-k+1,k)) pi[i] = k;

return pi;

}

Эффективный алгоритм

Этот алгоритм был разработан Кнутом (Knuth) и Праттом (Pratt) и независимо от них Моррисом (Morris) в 1977 г. (как основной элемент для алгоритма поиска подстроки в строке).

Первое важное замечание — что значение			не более чем на единицу превосходит значение		для любого
. Действительно, в противном случае, если бы			, то рассмотрим этот суффикс, оканчивающийся
в позиции	и имеющий длину	— удалив из него последний символ, мы получим суффикс,
оканчивающийся в позиции и имеющий длину			, что лучше	, т.е. пришли к
противоречию. Иллюстрация этого противоречия (в этом примере				должно быть равно 3):

Таким образом, при переходе к следующей позиции очередной элемент префикс-функции мог либо увеличиться на единицу, либо не измениться, либо уменьшиться на какую-либо величину. Уже этот факт позволяет нам

снизить асимптотику до — поскольку за один шаг значение могло вырасти максимум на единицу, то суммарно для всей строки могло произойти максимум увеличений на единицу, и, как следствие (т.к. значение никогда не

могло стать меньше нуля), максимум уменьшений. В итоге получится		сравнений строк, т.е. мы уже
достигли асимптотики	.

Но пойдём дальше, и избавимся от явных сравнений подстрок. Для этого постараемся максимально использовать информацию, вычисленную на предыдущих шагах.

Итак, пусть мы вычислили значение префикс-функции	для некоторого . Теперь, если	, то
мы можем с уверенностью сказать, что	, это иллюстрирует схема:

Пусть теперь, наоборот, оказалось, что	. Тогда нам надо попытаться попробовать подстроку
меньшей длины. В целях оптимизации хотелось бы сразу перейти к такой (наибольшей) длине		, что по-
прежнему выполняется префикс-свойство в позиции	, т.е.	:

Действительно, когда мы найдём такую длину , то нам будет снова достаточно сравнить символы				и
— если они совпадут, то	. Иначе нам надо будет снова найти меньшее (следующее по величине)
значение , для которого выполняется префикс-свойство, и так далее. Может случиться, что такие значения
кончатся, это происходит, когда	. В этом случае, если	, то	, иначе	.

Итак, общая схема алгоритма у нас уже есть, нерешённым остался только вопрос об эффективном нахождении таких

длин . Поставим этот вопрос формально: по текущей длине и позиции	(для которых выполняется
префикс-свойство, т.е.	) требуется найти наибольшее	,
для которого по-прежнему выполняется префикс-свойство:

После столь подробного описания, да и из картинки, уже весьма отчётливо видно, что это значение есть не что иное,

как	("-1" появляется из-за 0-индексации; впрочем, это ясно видно на рисунке), которое уже было
вычислено нами ранее. Таким образом, находить это мы можем за		.

Итак, мы окончательно построили алгоритм, который не содержит явных сравнений строк и выполняет действий. Реализация этого удивительно короткого алгоритма:

vector<int> prefix_function (string s) { int n = (int) s.length(); vector<int> pi (n);

for (int i=1; i<n; ++i) { int j = pi[i-1];

while (j > 0 && s[i] != s[j]) j = pi[j-1];

if (s[i] == s[j]) ++j; pi[i] = j;

}

return pi;

}

Как нетрудно заметить, этот алгоритм является онлайновым алгоритмом, т.е. он обрабатывает данные по ходу поступления — можно, например, считывать строку по одному символу и сразу обрабатывать этот символ, находя ответ для очередной позиции. Алгоритм требует хранения самой строки и предыдущих вычисленных значений префикс-функции, однако, как нетрудно заметить, если нам заранее известно максимальное значение, которое может принимать префикс-функция на всей строке, то достаточно будет хранить лишь на единицу большее количество первых символов строки и значений префикс-функции.

Применения

Поиск подстроки в строке. Алгоритм Кнута-Морриса-Пратта

Эта задача является классическим применением префикс-функции (и, собственно, она и была открыта в связи с этим).

Дан текст и строка	, требуется найти и вывести позиции всех вхождений строки в текст .
Образуем строку	, где символ	— это разделитель, который не должен нигде более
встречаться. Посчитаем для этой строки префикс-функцию. Теперь рассмотрим её значения, кроме
первых	(которые, как видно, относятся к строке и разделителю). По определению, значение

показывает наидлиннейшую длину подстроки, оканчивающейся в позиции 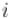и совпадающего с префиксом. Но в нашем случае это — фактически длина наибольшего блока совпадения со строкой и оканчивающегося в

позиции . Больше, чем	эта длина быть не может — за счёт разделителя. А вот
равенство	(там, где оно достигается), означает, что в позиции оканчивается искомое

вхождение строки (только не надо забывать, что все позиции отсчитываются в склеенной строке ).

Таким образом, если в какой-то позиции оказалось	, то в позиции
	строки начинается очередное вхождение
строки в строку .

Как уже упоминалось при описании алгоритма вычисления префикс-функции, если известно, что значения префикс-функции не будут превышать некоторой величины, то достаточно хранить не всю строку и префикс-функцию, а только её начало. В нашем случае это означает, что нужно хранить в памяти лишь строку и значение

префикс-функции на ней, а потом уже считывать по одному символу строку и пересчитывать текущее значение префикс-функции.

Итак, если длины строк и равны и соответственно, то алгоритм Кнута-Морриса-Пратта решает эту задачу за 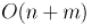времени и памяти.

Подсчёт числа вхождений каждого префикса

Здесь мы рассмотрим сразу две задачи. Дана строка 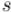длины . В первом варианте требуется для каждого префикса посчитать, сколько раз он встречается в самой же строке . Во втором варианте задачи дана

другая строка , и требуется для каждого префикса посчитать, сколько раз он встречается в .

Решим сначала первую задачу. Рассмотрим в какой-либо позиции значение префикс-функции в ней				.
По определению, оно означает, что в позиции	оканчивается вхождение префикса строки		длины	, и
никакой больший префикс оканчиваться в позиции не может. В то же время, в позиции			могло оканчиваться
и вхождение префиксов меньших длин (и, очевидно, совсем не обязательно длины			). Однако, как
нетрудно заметить, мы пришли к тому же вопросу, на который мы уже отвечали при рассмотрении алгоритма
вычисления префикс-функции: по данной длине	надо сказать, какой наидлиннейший её собственный суффикс
совпадает с её префиксом. Мы уже выяснили, что ответом на этот вопрос будет			. Но тогда и в этой задаче,
если в позиции оканчивается вхождение подстроки длины		, совпадающей с префиксом, то в также
оканчивается вхождение подстроки длины	, совпадающей с префиксом, а для неё применимы те
же рассуждения, поэтому в также оканчивается и вхождение длины			и так далее (пока индекс

не станет нулевым). Таким образом, для вычисления ответа мы должны выполнить такой цикл:

vector<int> ans (n+1); for (int i=0; i<n; ++i)

++ans[pi[i]];

for (int i=n-1; i>0; --i) ans[pi[i-1]] += ans[i];

Здесь мы для каждого значения префикс-функции сначала посчитали, сколько раз он встречался в массиве	, а
затем посчитали такую в некотором роде динамику: если мы знаем, что префикс длины встречался ровно	раз,

то именно такое количество надо прибавить к числу вхождений его длиннейшего собственного суффикса, совпадающего с его префиксом; затем уже из этого суффикса (конечно, меньшей чем длины) выполнится "пробрасывание"

этого количества к своему суффиксу, и т.д.

Теперь рассмотрим вторую задачу. Применим стандартный приём: припишем к строке строку 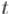через разделитель, т. е. получим строку , и посчитаем для неё префикс-функцию. Единственное отличие от первой задачи будет

в том, что учитывать надо только те значения префикс-функции, которые относятся к строке , т.е. все для .