
Алгоритмы C++
.pdf
if (to == root || match[to] != -1 && p[match[to]] != -1)
В этом случае нужно выполнить сжатие цветка. Выше уже подробно разбирался этот процесс, здесь приведём его реализацию:
int curbase = lca (v, to);
memset (blossom, 0, sizeof blossom); mark_path (v, curbase, to); mark_path (to, curbase, v);
for (int i=0; i<n; ++i)
if (blossom[base[i]]) { base[i] = curbase; if (!used[i]) {
used[i] = true; q[qt++] = i;
}
}
● Иначе — это "обычное" ребро, поступаем как и в обычном поиске в ширину. Единственная тонкость — при проверке, что эту вершину мы ещё не посещали, надо смотреть не в массив , а в массив — именно он заполняется для посещённых нечётных вершин. Если мы в вершину 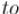 ещё не заходили, и она оказалась ненасыщенной, то мы нашли увеличивающую цепь, заканчивающуюся на вершине
ещё не заходили, и она оказалась ненасыщенной, то мы нашли увеличивающую цепь, заканчивающуюся на вершине 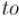 , возвращаем её.
, возвращаем её.
if (p[to] == -1) { p[to] = v;
if (match[to] == -1) return to;
to = match[to]; used[to] = true; q[qt++] = to;
}
Итак, полная реализация функции find_path():
int find_path (int root) {
memset (used, 0, sizeof used);

memset (p, -1, sizeof p); for (int i=0; i<n; ++i)
base[i] = i;
used[root] = true; int qh=0, qt=0; q[qt++] = root; while (qh < qt) {
int v = q[qh++];
for (size_t i=0; i<g[v].size(); ++i) { int to = g[v][i];
if (base[v] == base[to] || match[v] == to) continue;
if (to == root || match[to] != -1 && p[match[to]] != -1) { int curbase = lca (v, to);
memset (blossom, 0, sizeof blossom); mark_path (v, curbase, to); mark_path (to, curbase, v);
for (int i=0; i<n; ++i)
if (blossom[base[i]]) { base[i] = curbase; if (!used[i]) {
used[i] = true; q[qt++] = i;
}
}
}
else if (p[to] == -1) { p[to] = v;
if (match[to] == -1) return to;
to = match[to]; used[to] = true; q[qt++] = to;
}
}
}
return -1;
}
Наконец, приведём определения всех глобальных массивов, и реализацию основной программы нахождения наибольшего паросочетания:
const int MAXN = ...; // максимально возможное число вершин во входном графе
int n;
vector<int> g[MAXN];
int match[MAXN], p[MAXN], base[MAXN], q[MAXN]; bool used[MAXN], blossom[MAXN];
...
int main() {
... чтение графа ...
memset (match, -1, sizeof match); for (int i=0; i<n; ++i)
if (match[i] == -1) {
int v = find_path (i); while (v != -1) {
int pv = p[v], ppv = match[pv]; match[v] = pv, match[pv] = v; v = ppv;
}
}
}
Оптимизация: предварительное построение паросочетания
Как и в случае Алгоритма Куна, перед выполнением алгоритма Эдмондса можно каким-нибудь простым алгоритмом построить предварительное паросочетание. Например, таким жадным алгоритмом:
for (int i=0; i<n; ++i) if (match[i] == -1)
for (size_t j=0; j<g[i].size(); ++j) if (match[g[i][j]] == -1) {

match[g[i][j]] = i; match[i] = g[i][j]; break;
}
Такая оптимизация значительно (в несколько раз) ускорит работу алгоритма на случайных графах.
Случай двудольного графа
В двудольных графах отсутствуют циклы нечётной длины, и, следовательно, код, выполняющий сжатие цветков, никогда не выполнится. Удалив мысленно все части кода, обрабатывающие сжатие цветков, мы получим Алгоритм
Куна практически в чистом виде. Таким образом, на двудольных графах алгоритм Эдмондса вырождается в алгоритм Куна и работает за 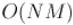 .
.
Дальнейшая оптимизация
Во всех вышеописанных операциях с цветками легко угадываются операции с непересекающимися множествами, которые можно выполнять намного эффективнее (см. Система непересекающихся множеств). Если переписать алгоритм
с использованием этой структуры, то асимптотика алгоритма понизится до |
. Таким образом, для |
произвольных графов мы получили ту же асимптотическую оценку, что и в случае двудольных графов (алгоритм Куна), но заметно более сложным алгоритмом.

Покрытие путями ориентированного ациклического графа
Дан ориентированный ациклический граф . Требуется покрыть его наименьшим числом путей, т.е. найти наименьшее по мощности множество непересекающихся по вершинам простых путей, таких, что каждая вершина принадлежит какому-либо пути.
Сведение к двудольному графу
Пусть дан граф |
с вершинами. Построим соответствующий ему двудольный граф |
стандартным образом, т.е.: |
||||||||
в каждой доле графа |
будет по |
|
вершин, обозначим их через |
|
и соответственно. Тогда для каждого ребра |
|||||
исходного графа |
проведём соответствующее ребро |
|
. |
|
|
|
||||
Каждому ребру |
соответствует одно ребро |
, и наоборот. Если мы рассмотрим в |
любой |
|
|
|||||
путь |
|
, то ему ставится в соответствие набор рёбер |
|
|
. |
|||||
Более просто для понимания будет, если мы добавим "обратные" рёбра, т.е. образуем граф |
из графа |
|||||||||
добавлением рёбер вида |
|
|
|
. Тогда пути |
|
|
в графе |
|
||
будет соответствовать путь |
|
|
|
|
. |
|
|
|
||
Обратно, рассмотрим любой путь |
|
в графе |
, начинающийся в первой доле и заканчивающийся во второй |
|||||||
доле. Очевидно, |
снова будет иметь вид |
|
|
|
, и ему можно поставить |
|||||
в соответствие в графе |
путь |
|
|
. Однако здесь есть одна тонкость: |
могло совпадать с |
|||||
, поэтому путь |
получился бы циклом. Однако по условию граф |
ациклический, поэтому это вообще |
||||||||
невозможно (это единственное место, где используется ацикличность графа ; тем не менее, на циклические |
||||||||||
графы описываемый здесь метод вообще нельзя обобщить). |
|
|
|
|
|
|||||
Итак, всякому простому пути в графе |
, начинающемуся в первой доле и заканчивающемуся во второй, можно |
|||||||||
поставить в соответствие простой путь в графе |
, и наоборот. Но заметим, что такой путь в графе |
— |
||||||||
это паросочетание в графе |
. Таким образом, любому пути из |
|
можно поставить в соответствие паросочетание |
|||||||
в графе , и наоборот. Более того, непересекающимся путям в |
соответствуют непересекающиеся паросочетания |
|||||||||
в . |
|
|
|
|
|
|
|
|
|
|
Последний шаг. Заметим, что чем больше путей есть в нашем наборе, тем меньше все эти пути содержат рёбер. А именно, если есть 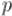 непересекающихся путей, покрывающих все
непересекающихся путей, покрывающих все 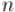 вершин графа, то они вместе
вершин графа, то они вместе

содержат |
рёбер. Итак, чтобы минимизировать число путей, мы должны максимизировать |
|
число рёбер в них. |
|
|
Итак, мы свели задачу к нахождению максимального паросочетания в двудольном графе |
. После нахождения |
|
этого паросочетания (см. Алгоритм Куна) мы должны преобразовать его в набор путей в |
(это делается |
|
тривиальным алгоритмом, неоднозначностей здесь не возникает). Некоторые вершины могут остаться ненасыщенными паросочетанием, в таком случае в ответ надо добавить пути нулевой длины из каждой из этих вершин.
Взвешенный случай
Взвешенный случай не сильно отличается от невзвешенного, просто в графе на рёбрах появляются веса, и требуется найти уже паросочетание наименьшего веса. Восстанавливая ответ аналогично невзвешенному случаю, мы получим покрытие графа наименьшим числом путей, а при равенстве — наименьшим по стоимости.


Теорема Татта гласит: в графе 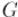 существует совершенное паросочетание тогда и только тогда, когда многочлен
существует совершенное паросочетание тогда и только тогда, когда многочлен  не равен нулю тождественно (т.е. имеет хотя бы одно слагаемое с ненулевым коэффициентом).
не равен нулю тождественно (т.е. имеет хотя бы одно слагаемое с ненулевым коэффициентом).
Канадский математик Вильям Томас Татт (William Thomas Tutte) первым указал на тесную связь между паросочетаниями в графах и определителями матриц (1947 г.). Более простой вид этой связи позже обнаружил Эдмондс (Edmonds) в случае двудольных графов (1967 г.).
Практическое применение: рандомизированный алгоритм
Непосредственно применять теорему Татта даже в задаче проверки существования совершенного паросочетания нецелесообразно. Причиной этого является то, что при символьном вычислении определителя (т.е. в виде многочленов над переменными 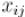 ) промежуточные результаты являются многочленами, содержащими
) промежуточные результаты являются многочленами, содержащими
переменных. Поэтому вычисление определителя матрицы Татта в символьном виде потребует неоправданно много времени.
Венгерский математик Ласло Ловас (Laszlo Lovasz) был первым, указавшим возможность применения здесь рандомизированного алгоритма для упрощения вычислений.
Идея очень проста: заменим все переменные 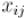 случайными числами:
случайными числами:
|
|
|
Тогда, если полином |
был тождественно нулевым, после такой замены он и будет оставаться нулевым; если |
|
же он был отличным от нуля, то при такой случайной числовой замене вероятность того, что он обратится в |
||
ноль, достаточно мала. |
|
|
Понятно, что такой тест (подстановка случайных значений и вычисление определителя |
) если и ошибается, |
|
то только в одну сторону: может сообщить об отсутствии совершенного паросочетания, когда на самом деле оно существует.
Мы можем повторить этот тест несколько раз, подставляя в качестве значений переменных новые случайные числа, и с каждым повторным запуском мы получаем всё большую уверенность в том, что тест выдал правильный ответ.
На практике в большинстве случаев достаточно одного теста, чтобы определить, есть ли в графе совершенное паросочетание или нет; несколько таких тестов дают уже весьма высокую вероятность.
Для оценки вероятности ошибки можно использовать лемму Шварца-Зиппеля (Schwartz–Zippel), которая гласит, что вероятность обращения в ноль ненулевого полинома -ой степени при подстановке в качестве значений переменных случайных чисел, каждое из которых может принимать  вариантов значения, — эта вероятность удовлетворяет неравенству:
вариантов значения, — эта вероятность удовлетворяет неравенству:

|
|
|
|
Например, при использовании стандартной функции случайных чисел C++ |
получаем, что эта вероятность |
||
при |
составляет около процента. |
|
|
Асимптотика решения получается равной |
(с использованием, например, алгоритма Гаусса), умноженное |
||
на количество итераций теста. Стоит отметить, что по асимптотике такое решение значительно отстаёт от решения алгоритмом Эдмондса сжатия цветков, однако в некоторых случаях более предпочтительно из-за
простоты реализации.
Восстановить само совершенное паросочетание как набор рёбер является более сложной задачей. Самым простым, хотя и медленным, вариантом будет восстановление этого паросочетания по одному ребру: перебираем первое ребро ответа, выбираем его так, чтобы в оставшемся графе существовало совершенное паросочетание, и т. д. Более эффективные алгоритм построили Рабин (Rabin) и Вазирани (Vazirani) в 1984 и 1989 г., но здесь
они рассматриваться не будут.
Доказательство теоремы Татта
Чтобы хорошо понять доказательство этой теоремы, сначала рассмотрим более простой результат, — полученный Эдмондсом для случая двудольных графов.
Теорема Эдмондса
Рассмотрим двудольный граф, в каждой доле которого по вершин. Составим матрицу |
, в которой, |
|
по аналогии с матрицей Татта, |
является отдельной независимой переменной, если ребро |
присутствует в |
графе, и является тождественным нулём в противном случае.
Эта матрица похожа на матрицу Татта, однако матрица Эдмондса имеет вдвое меньшую разность, и каждому ребру здесь соответствует только одна ячейка матрицы.
Докажем следующую теорему: определитель |
отличен от нуля тогда и только тогда, когда в двудольном |
графе существует совершенное паросочетание. |
|
Доказательство. Распишем определитель согласно его определению, как сумма по всем перестановкам:


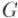 с
с 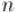 вершинами (
вершинами (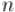 — чётно).
— чётно).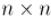 :
: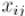 ( ) — это либо независимая переменная, соответствующая ребру между вершинами
( ) — это либо независимая переменная, соответствующая ребру между вершинами  и , либо тождественный ноль, если ребра между этими вершинами нет.
и , либо тождественный ноль, если ребра между этими вершинами нет.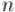 вершинами матрица Татта содержит
вершинами матрица Татта содержит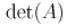 матрицы Татта. Это, вообще говоря, многочлен относительно переменных
матрицы Татта. Это, вообще говоря, многочлен относительно переменных 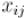 .
.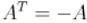 , и теперь получаем цепочку равенств:
, и теперь получаем цепочку равенств: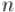 определитель необходимо должен быть равен нулю.
определитель необходимо должен быть равен нулю. матрицы Татта представляет собой квадрат от суммы слагаемых такого вида, что каждое слагаемое
матрицы Татта представляет собой квадрат от суммы слагаемых такого вида, что каждое слагаемое