физика механика

начало ое-2

Обычно интерес представляет только изменение энтропии. При переходе из состояния 1, которому отвечает вероятность w1 , в

состояние 2, которому отвечает вероятность w2 , энтропия изменяется от S1 до S2 . Тогда из формулы Больцмана следует,

что

(5.73) S = S2 − S1 = k ln w2 . w1

Из формулы (5.73) вытекает следующее статистическое толкование второго начала термодинамики (в любой формулировке):

9 термодинамическая вероятность состояния замкнутой системы при всех происходящих в ней процессах не может убывать;

9 при любом процессе, который протекает в замкнутой системе и переводит ее из состояния 1 в состояние 2, изменение w термодинамической вероятности w положительно (для необратимого процесса) или равно нулю (для обратимого процесса): w = w1 − w2 ≥ 0 .

Необратимые процессы протекают самопроизвольно до тех пор, пока система не достигнет состояния, которому отвечает наибольшая вероятность; энтропия при этом достигает своего максимума. Вот некоторые примеры таких процессов.

Пример 10. Полное перемешивание молекул двух газов в результате диффузии.

Пример 11. Выравнивание температур двух тел с различными исходными температурами.

Таким образом, энтропия характеризует вероятность, с которой устанавливается то или иное состояние. Кроме того, энтропия является мерой хаотичности или необратимости.

*Второе начало термодинамики, установленное для замкнутых систем на Земле, не может быть распространено на всю бесконечную Вселенную. Такое распространение приводит к неправильному с физической и философской точек зрения выводу о том, что температура всех тел во Вселенной должна выравняться. При этом все формы движения, кроме хаотического теплового движения, должны прекратиться («тепловая смерть Вселенной» согласно Клаузиусу). В

действительности, в связи с бесконечностью Вселенной, как показал Больцман, в некоторых ее частях неизбежны

- 141 -

флуктуации (колебания термодинамических параметров около средних значений), которые нарушают тепловое равновесие. Продолжительность и величина этих флуктуаций могут быть весьма значительны. Вспомните природные катаклизмы наших дней, то тут, то там непредсказуемо возникающие на Земле. Доказано, что для бесконечной Вселенной не может быть равновесного состояния, соответствующего «тепловой смерти».

***** Глава5. §9 *****

§10. Понятие о третьем начале термодинамике

Энтропия как однозначная функция состояния системы вводится с помощью дифференциального соотношения (5.66). Поэтому она может быть определена лишь с точностью произвольной константы, которая не может быть найдена из первого или второго начала термодинамики. В связи с этим оказывается невозможным определение абсолютного значения энтропии.

Экспериментальное изучение свойств веществ при сверхнизких температурах (T < 1K ) привело к установлению

третьего закона термодинамики или принципа Нернста (1906

г.): при любом изотермическом процессе, проведенном при абсолютном нуле температуры, изменение энтропии равно нулю:

S T →0 = 0 и S =S0= const

независимо от изменения любых параметров состояния (например, давления, объема, напряженности внешнего поля и т.

д.).

Третье начало не позволяет находить абсолютное значение энтропии. Однако, постоянство энтропии при T → 0 позволяет выбрать эту константу за начало отсчета значений энтропии и, тем самым, определять изменение энтропии в исследуемых процессах.

Из третьего начала термодинамики следует очень важный вывод (пожалуй, важнее, чем сам закон): невозможен такой

процесс, в результате которого тело могло бы быть охлаждено до абсолютного нуля (принцип недостижимости абсолютного нуля температуры). На это указывает тот факт, что при абсолютном нуле температуры обращаются в нуль для любого вещества теплоемкость при постоянном объеме и коэффициент

- 142 -

	объемного расширения.
			***** Глава5. §10 *****
		§11. Основное уравнение молекулярно-
		кинетической теории газов
	Возвращаясь к кинетической теории газов, сделаем
	некоторые дополнения к тому, что уже было сказано в §1 этой
	главы.
	● Кинетическая теория газов
	Учение о строение и физических свойствах газов, основанное
	на статистическом методе исследования. В основе
	классической статистической физики лежат следующие
	исходные положения:
		9 в системе частиц выполняются законы сохранения
		энергии, импульса и момента импульса;
		9 все физические процессы в системе частиц протекают в
		пространстве и во времени непрерывно (например,
		скорость и энергия любой частицы могут непрерывно
		изменяться под действием различных сил);
		9 любая частица в системе является «меченой», то есть ее
				можно		отличить			от всех
	y			остальных			таких			же
		N молекул газа в объеме V=L3		частиц		и	проследить			ее
				траекторию от				начала		до
				конца движения;
				9	любая				частица
		L		системы			может		иметь
		L
				произвольные				значения
				координат			и	импульсов
	z	L	L	(или				скоростей)
			x				от
	К выводу основного уравнения			независимо				значений
				этих	величин для				других
		кинетической теории газов
				частиц.
	Рассмотрим модель, в которой молекулы газа представляют
	собой безразмерные упругие шарики. В промежутках между
	абсолютно упругими соударениями друг с другом или со стенками
	сосуда	молекулы	двигаются	равномерно		и	прямолинейно,
			- 143 -

поскольку никакие силы на них не действуют. Соударения молекул со стенками сосуда и создают давление p газа.

Если	p – давление газа, V		– объем сосуда, в котором
находится газ, m = mмN –		масса	газа, mм – масса молекулы,
ρ = m V	– плотность газа,	N –	число молекул, n0 = N V –

концентрация молекул (их число в единице объема), k – постоянная Больцмана, T – термодинамическая температура газа,

то в кубе объемом V = L3 содержится N молекул газа, причем можно считать, что в направлении каждой из трех осей пространственной системы координат движется N3 молекул (см.

рис.).

Предположим, что молекула пролетает со скоростью υ путь от одной стенки сосуда до противоположной и обратно, равный 2l . Время между соударениями с одной и той же стенкой

определится тогда по	формуле	t = 2L υ .	Следовательно, в
единицу времени происходит 1		t =υ 2L ударов о стенку.		При
каждом ударе скорость	молекулы меняет		знак, то есть	+υ

заменяется на −υ ; следовательно, импульс + mмυ заменяется на − mмυ . Таким образом, при каждом соударении молекулы со стенкой последней передается импульс 2mмυ .

За промежуток времени t со стенкой соударяется N3 молекул, которые передают ей импульс, равный

(5.74)

q = 2m

υ

υ

t

N

.

м

2L

3

r

r

Согласно второму закону Ньютона

r

сила,

p = mм

υ

= F t

действующая на стенку, в наших обозначениях равна

(5.75)

F =

q

=

Nm υ2

t

м .

3L

В качестве квадрата скорости следует брать средний квадрат скорости υ2 , поскольку молекулы обладают разными скоростями.

Учитывая,	что давление	p = F L2 ,				находим				p = Nmмυ2 3l 3 .
Подставив	m = mмN и	L3 =V ,				получим				давление газа в
дополнение к формуле (5.4:		p = n0kT ):
		p =	m
	(5.76)			υ2		=	ρυ2		.
			3V
						3
		- 144 -

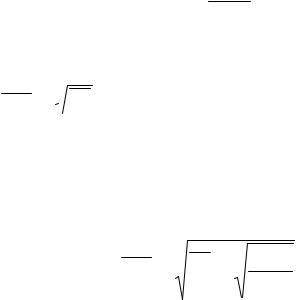
Таким образом, в замкнутой системе давление газа пропорционально или среднему квадрату скорости, или температуре.

Из уравнения (5.76) следует основное уравнение кинетической теории газов – произведение давления газа на

занимаемый им объем есть две трети кинетической энергии поступательного движения всех молекул газа:

(5.77) pV = 23 m2υ2 = 23WK .

С помощью формулы (5.76) по легко измеряемым величинам p , m и V можно найти среднюю квадратичную скорость

молекул υкв = υ2 .

Используя закон Менделеева-Клапейрона (5.3) и формулу (5.77), легко найти явное выражение для средней

	квадратичной скорости молекул:			pV =	2 mυ2		=	m	RT ,
					3 2			μ
	(5.78)		υкв = υ2 =	3RT .
				μ
		*****	Глава5. §11 *****

§12. Закон распределения молекул по скоростям. Скорости молекул

Движение молекул газа подчиняется законам статистической физики. В каждый момент времени энергии и скорости отдельных молекул могут значительно отличаться от средних значений.

С помощью теории вероятности Максвеллу удалось вывести формулу для относительной частоты, с которой в газе при данной температуре встречаются молекулы со скоростями в определенном интервале значений.

Если N – общее число молекул газа, dN – число молекул, скорости которых заключены в определенном интервале, υx ,υy ,υz – нижняя граница интервала скоростей по осям x, y, z ,

dυx ,dυy ,dυz – величина интервала скоростей, T – температура газа, e = 2,718.... – основание натуральных логарифмов,

- 145 -

k = 1,38 10−23 Дж К

–

постоянная

Больцмана, mм – масса

молекулы, то закон распределения Максвелла запишется в виде:

m

3 2

−

m υ2

(5.79)

м

dN = N

м

e

2kT dυxdυydυz =

2πkT

m

υ2

mмυ2y

m

υ2

mм e−

м x

mм

e− 2kT

м z

= N

2kT

mм e− 2kT dυ

x

dυ

y

dυ

z

=

2πkT

2πkT

2πkT

= Nf (υx )f (υy )f

(υz )dυxdυxdυx ,

так

как распределение

молекул

по

проекциям скоростей

υi

( i = x,y,z )

взаимно

независимы,

и функцию

f (υi )

называют

функцией распределения Максвелла по проекциям скоростей на

соответствующую ось, где

2

m υ

f (υi )=

м

i

(5.80)

mм e− 2kT .

2πkT

Распределения Максвелла изотропно. Это проявляется в том, что

функция f (υx ,υy ,υz )

зависит

только

от

модуля

скорости,

следовательно, функция Максвелла для модуля скорости имеет

вид:

m υ2

m

3 2 −

(5.81)

м

4πυ2 .

f (υ)=

м

e

2kT

2πkT

Закон распределения молекул идеального газа по скоростям,

теоретически

установленный

Максвеллом,

показывает,

какое

число молекул dN из общего числа N его молекул обладает при

данной температуре скоростью,

заключенной в интервале от υ до

dN

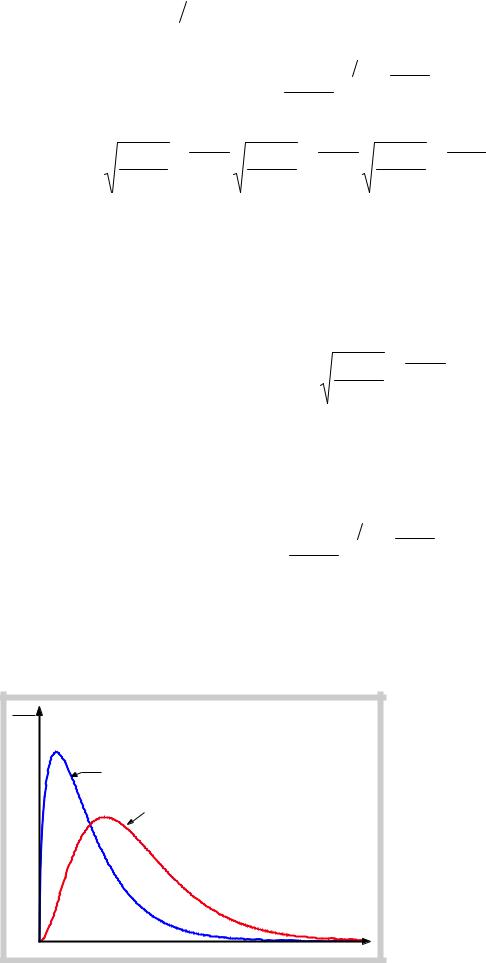
Функция

распределения Максвелла

υ + dυ .

График

функции

dν

при

разных

температурах

распределения

T1

асимметричен.

T2 >T1

Положение

максимума

характеризует наиболее

часто

встречающуюся

скорость,

которую

называют

наиболее

ν

вероятной

скоростью

υm .

Скорости

- 146 -

превышающие υm встречаются чаще, чем меньшие скорости.

С повышением температуры максимум распределения

сдвигается в направлении больших скоростей. Одновременно

кривая становится более плоской (площадь, заключенная под

кривой, не может измениться,

так как число молекул N остается

постоянным).

Для определения наиболее вероятной скорости нужно

исследовать на максимум функцию распределения Максвелла

(5.81), то есть приравнять первую производную к нулю и решить

относительно υ :

m

3 2

d

−

mмυ2

(5.82)

2kT

= 0

м

υ2e

2πkT

dυ

υ=υ

В результате получаем:

m

(5.83)

υm =

2kT =

2RT

=

2RT .

mм

NAmм

μ

При расчетах используется не мгновенная скорость

отдельной молекулы, а некоторое среднее значение. Если

определить долю внутренней энергии газа, приходящуюся на одну

молекулу

(считая,

dN

Положение

различных скоростей

что

все

молекулы

на кривой

Максвелла

обладают

dν

одинаковой

энергией),

то

она

оказывается

пропорциональной

νm...νкв

квадрату

скорости

ν

молекулы

(W ~ υ2 ).

<ν>

Квадратный корень

из среднего квадрата скорости, как мы уже определили в §11 этой

главы, называется средней квадратичной скоростью (см. формулу

(4.78)).

Используя функцию распределения Максвелла (5.81), можно

получить среднюю арифметическую скорость молекул газа:

(5.84)

∞

(υ)dυ =

8kT

8RT .

<υ >= ∫υf

=

0

πmM

π

- 147 -

Взаимное положение характерных скоростей на кривой Максвелла представлено на рисунке выше.

***** Глава5. §12 *****

§13. Энергия молекул. Закон равномерного распределения энергии по степеням свободы. Внутренняя энергия и удельная теплоемкость

В соответствии с основным уравнением кинетической теории газов (5.77) кинетическая энергия отдельной молекулы

определяется как W = m υ2							2 (в качестве υ2 берется среднее
					к	м
значение				= (3RT )
	υ2					μ.
Если					– средняя		кинетическая энергия отдельной
				Wк
молекулы,		k = 1,38 10−23 Дж К – постоянная Больцмана, T –

температура газа, то получаем, что средняя кинетическая энергия отдельной молекулы идеального газа равна

(5.85)			1 m			3 kT .
		=		υ2	=
	W
	к		2 м			2

С помощью формулы (5.83) находим наиболее вероятную энергию отдельной молекулы

(5.86) Wmк = 12 mмυm2 = kT .

Таким образом, температура газа пропорциональна средней кинетической энергии его молекул T ~ Wк 53.

В общем случае можно утверждать: абсолютная температура является мерой кинетической энергии молекул; абсолютному нулю температуры (0 К) отвечает равная нулю кинетическая энергия молекул.

Формула (5.85) выведена для случая одноатомного идеального газа. Каждая молекула такого газа обладает тремя степенями свободы, то есть может совершать поступательное движение во всех трех направлениях в пространственной системе координат.

Число степеней свободы i определяется числом координат, однозначно задающих состояние движения.

53Эта закономерность справедлива также для жидкостей и твердых тел

-148 -

Согласно Клаузиусу и Максвеллу, энергия молекулы

равномерно распределяется между всеми степенями свободы

(принцип равнораспределения). Значит, на каждую степень свободы одноатомной молекулы приходится в среднем энергия

W = kT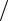2 .

Справочная таблица. Число степеней свободы

Вещество				Тип движения						Всего
		Поступательно		Вращательное			Колебательное
			е
Одноатомный газ			3		–			–			3
Двухатомный			3		2			–			5
газ54
Трехатомный			3		3			–			6
газ55
Твердое тело			–		–			6			6
Жидкость					Не
				определено
Под внутренней энергией тела понимается суммарная
энергия его молекул (см. §3 этой главы).
Если	U ν	– внутренняя энергия в расчете на							один		моль
вещества,	ν = m μ −		количество		молей,		m	– масса,			R –
универсальная газовая постоянная,					T – температура,				i –		число
степеней свободы, NA − количество молекул газа в одном моле,
то	(5.87)		U ν = NАWК = NАikT 2 = RiT 2.
Сравнивая		(5.87) с выражением (5.17)						для	внутренней

энергии, получаем выражение для молярной теплоемкости при постоянном объеме:

(5.88)	CV =	i	R.
	2
Применяя уравнение	Майера		(5.20), нетрудно найти

выражение для молярной теплоемкости при постоянном давлении:

(5.89) Cp = i +2 2 R.

***** Глава5. §13 *****

54Воздух, состоящий из смеси газов, принимают за двухатомный газ

55Исключение: СО2 имеет столько же степеней свободы, как и двухатомный газ

-149 -

§14. Число соударений и длина свободного пробега. Среднее число соударений. Средняя длина свободного пробега

Молекула газа двигается прямолинейно, пока не произойдет встреча с другой молекулой. Рассчитаем среднюю частоту соударений (среднее число соударений).

Если z – среднее число соударений, равное отношению числа соударений ко времени, за которое это число соударений произошло, d – диаметр молекулы, υ – средняя скорость молекул, n = NV – концентрация молекул, NA – постоянная Авогадро, ρ – плотность газа, μ – молярная масса, T – температура газа, p – давление газа, то число соударений

молекулы, обладающей скоростью υ (в предположении, что все остальные молекулы в это время покоятся), определяется числом

молекул, центры которых находятся в
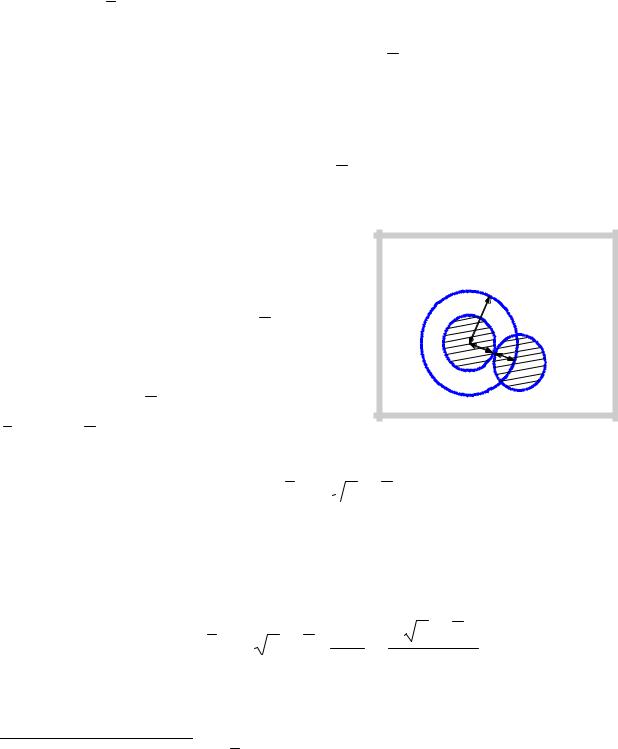
объеме, пролетаемом молекулой за						К вычислению среднего
время	t .	Этот	объем	представляет		числа соударений молекул
собой	цилиндр		с	основанием		d
площадью d 2π и длиной υ t . Число
молекул в этом объеме, или число						r r
соударений		за	время	t ,	равно
N = nV = nd 2πυ t . Отсюда					находим

z = nd 2πυ . Учитывая, что остальные молекулы на самом деле двигались, получаем среднее число соударений56

(5.90) z = π 2d 2υn,

или, поскольку

n =	N	=		m		= mN A =		ρN A ,
	V		m V
							Vμ	μ
получаем				м
								π 2d 2υρ .
(5.91)	z = π			2d	2υρ		N A =
							μ	kT

Расстояние, проходимое молекулой в среднем между двумя соударениями, называется средней длиной свободного пробега.

56Среднее число соударений z для большинства газов при нормальных условиях составляет от 109 до 1010 с-1

-150 -