физика механика

где s −длина пути,

отсчитываемая вдоль траектории от начала

рассматриваемого участка точки приложения силы (см.

рис. выше).

Для вычисления этого интеграла необходимо знать зависимость

1.055

Fτ

от s вдоль

Графическое представление силы

данной траектории

и произведенной этой

силой работы на участке пути s1...s

2

1.05

L (см. рис. выше).

Работа А

(Площадь под кривой)

Если

эта

1.045

F =Bs0.01

зависимость

τ

представлена

1.04

(B=1H*м−0.01)

,H

графически,

то

τ

F

1.035

искомая работа A

1.03

выражается

1.025

площадью

под

кривой,

s1

1.02

s2

заштрихованной

20

30

40

50 s,м 60

70

80

90

100

10

На представленном рисунке работа

на

рисунке

слева.

s

1,01 80

(801,01 − 301,01 )≈ 52(Дж).

A = B∫ s0,01ds = B s

=

B

0

1,01

30

1,01

Силы делятся на потенциальные и непотенциальные.

● Потенциальные силы

Такие силы, работа которых зависит только от начальных и конечных положений точек их приложения и не зависит ни от вида траекторий этих точек, ни от законов их движения по траекториям.

Например, силы взаимодействия материальных точек системы потенциальны, если они зависят только от конфигурации системы, то есть от взаимного расположения всех точек системы, причем работа этих сил при перемещении системы из одного произвольного положения в другое не зависит от способа перемещения, а полностью определяется начальной и конечной конфигурациями системы. Примерами такого рода являются силы гравитационного и электростатического взаимодействий.

Работа потенциальный силы при перемещении точки ее приложения вдоль любой замкнутой траектории (например, 1а2b1 на рисунке ниже) равна нулю (применен знак интеграла ∫... по

- 61 -

замкнутому пути):			∫Fdrr ≡ 0					2.
(3.5)	A1a2b1 =
			(L)
● Непотенциальные силы								.
	Такие	силы,		работа			a
	которых		при	любых
							.	b
	перемещениях
	замкнутой		системы					Иллюстрация
	всегда	отрицательна. К						работы потенциальной
	непотенциальным						силы при перемещении
							точки ее приложения вдоль
	относятся,		в частности,		1	замкнутой траектории 1a2b1
	диссипативные			силы. .
	Таковы, например, силы трения скольжения и силы
	сопротивления движению тел в жидкостях и газах.
	Диссипативные силы, в отличие от потенциальных,
	зависят не только от взаимного расположения
	взаимодействующих сил, но и от их относительных
	скоростей.
● Консервативная механическая система
	Такая система, в которой все внутренние силы
	потенциальны, а все внешние силы потенциальны и
	стационарны (не зависят от времени). Системы, не
	удовлетворяющие указанным условиям, называются
	неконсервативными.
● Мощность силы
	Характеристика работы силы, совершаемой за единицу
	времени.
● Мгновенная мощность							N ,
	Скалярная		физическая величина					равная отношению
	элементарной работы δA к малому промежутку времени
	dt , в течение которого эта работа совершается:

(3.6) N = δdAt = Frυr = Fτυ .

- 62 -

Пример 1. Найти величину суммарной диссипативной силы Fдс при движении автомобиля с постоянной

скоростью υ = 72 км/ч, если его мощность	N = 40 кВт.
Какому закону Ньютона подчиняется	движение

автомобиля?

aПримем автомобиль за материальную точку, движущуюся с постоянной скоростью. Движение с постоянной скоростью стало возможным, когда сила тяги двигателя уравновесила суммарную силу трения, направленную противоположно силе тяги. Следовательно, движение автомобиля подчиняется I-ому закону Ньютона. Для нахождения же суммарной диссипативной силы (суммарной силы трения) необходимо воспользоваться III-им законом Ньютона и формулой (3.6):

	F =	N	,		F =	4 104	= 2 103 (Н)= 2 (кН).
		υ				20
	дс				дс
					***** Глава3. §2		*****

§3. Кинетическая энергия

● Кинетическая энергия тела

Энергия его механического движения.

Получим вначале выражение кинетической энергии WMT

материальной точки, воспользовавшись выражением (3.3). Вспомните, это выражение устанавливает связь пространственной и временной характеристик действия силы на точку:

(3.7) dW	r	r r	r	mυr2			mυ2
	= δA =υ	dp =υ	d(mυ)= d				= d
	MT				2			2

.

В ньютоновской26 механике m = const , поэтому

(3.8) W =	mυ2	.
MT	2

Для системы, состоящей из n материальных точек, необходимо просуммировать кинетические энергии всех этих точек, если i -ая точка имеет скорость и массу соответственно υi и

mi :

26О кинетической энергии в релятивистской механике см. главу 4

-63 -

(3.9)			n		m υ2
	W	= ∑			i i	.
	сис		i=1 2
Кинетическая энергия WT абсолютно твердого тела:
(3.10)	W =	1	∫	ρυ2dV ,
	Т	2
			(V )
где υ − скорость точек	малого	элемента dV объема тела
плотностью ρ и массой dm = ρdV ,		а интегрирование проводится

по всему объему V тела.

Но для какого случая движения (поступательного или вращательного) справедливы формулы (3.9) и (3.10)? Ответ: для любого.

Если абсолютно твердое тело движется поступательно со скоростью υ , то его кинетическая энергия

(3.11) W пост =	mυ2	.
k	2
Если то же тело вращается относительно неподвижных точки
О или оси OZ? Можно воспользоваться аналогией, работающей

между физическими величинами в случаях поступательного и

вращательного движений:		m → JO или m → JZ , υ → ω , где m и
JO (JZ )− масса и момент инерции тела относительно полюса О
или оси OZ. Тогда имеем выражения для кинетической энергии
тела, вращающегося		относительно		полюса W вр				или
относительно оси W вр:						kO
kZ
(3.12) W вр =	JOω2		или (3.13)	W вр =	JZω2		.
kO		2		kZ	2

Если же тело находится одновременно в состоянии поступательного и вращательного движений, то можно воспользоваться теоремой Кенига: кинетическая энергия абсолютно твердого тела Wk равна сумме кинетических энергий –

поступательного движения этого тела со скоростью υC его центра инерции и вращения этого тела относительно центра инерции:

(3.14) W =	mυ2	J ω2
	C +	C .
k	2	2

Пример 2. Определить относительно неподвижной системы координат кинетическую энергию однородного

- 64 -

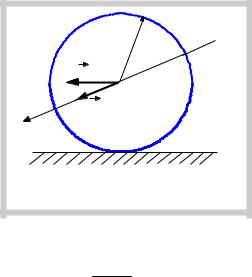
шара массы m , катящегося по горизонтальной плоскости
без проскальзывания с постоянной скоростью υ .
aОчевидно, скорость центра инерции шара υc =υ ; угловая
скорость вращения относительно оси OZ, совпадающей с осью
инерции,	−ω, радиус шара − R и
момент инерции		− 2 mR2 .		Условие					R
		5					vC	.O
движения	без	проскальзывания:
υC = ωR ,	так	как	точка		C		ω		m
								.C
соприкосновения		шара			с	Z
поверхностью		имеет		нулевую
скорость (точка C в момент контакта							ДВИЖЕНИЕ ШАРА
						ПО ГОРИЗОНТАЛЬНОЙ ПЛОСКОСТИ
принадлежит и шару, и поверхности,
по которой он катится).
(3.15)	W = mυC2		+ JCω2		= mυC2	+ 2 mR2 υC2			= 0,7mυ2 .
	k	2		2	2	5	2R2		C
Изменение кинетической энергии механической системы
равно алгебраической сумме работ всех внешних и внутренних
сил, действующих на эту систему: dWk = δAвнут +δAвнеш. Однако
если тело является абсолютно твердым, то работа внутренних сил
в соответствии с третьим законом Ньютона тождественно равна
нулю (по аналогии с законом изменения импульса, когда только
внешние силы приводят к изменению состояния временной
характеристики силы – импульса).

§4. Потенциальная энергия системы

● Потенциальная энергия системы

Часть энергии механической системы, зависящая только от ее конфигурации, то есть от взаимного расположения всех материальных точек системы и от их положения во внешнем потенциальном поле. Убыль потенциальной энергии при перемещении системы из произвольного положения 1 в другое произвольное положение 2 измеряется той работой A12 , которую

совершают при этом все потенциальные силы (внутренние и внешние), действующие на систему:

(3.16) Wп(1)−Wп(2)= A12 ,

где Wп(1) и Wп(2)− значения потенциальной энергии системы в начальном и конечном положениях. Соответственно, работа

- 65 -

потенциальных сил при малом изменении конфигурации системы

равна:

(3.17)

δAпот = −dWп.

упругости

В механике

потенциальными

являются

силы

и

упруго деформированное тело

гравитации (см. § 2

главы 2).

Fупр.

Рассмотрим

O.

dx

работу сил упругости

.

.

X

при

деформации

x1

x2

удлинения

(сжатия)

К РАСЧЕТУ РАБОТЫ СИЛ УПРУГОЙ ДЕФОРМАЦИИ

упругого тела (см.

рис.):

формулу

(2.3)

и

= x2

− Fdx = x2

− kxdx = − k (x2

− x2 ).

(3.18)

A

=

F ds

упр

∫ τ

∫

∫

2

2

1

( L)

x1

x1

При x1 = 0 и

x2 = x

имеем более общее выражение для работы

сил упругости:

k

′

Aупр = −

x

2

.

(3.18 )

2

Знак минус указывает на то, что работа совершена над пружиной.

Потенциальная же энергия упруго деформированной пружины в

соответствии с выражением (3.17) равна

(3.19)

Wупр = k x2 , то есть положительна!

2

Рассмотрим работу сил гравитации при перемещении тела

массой m из точки 1 в точку 2 поля сил тяготения некоторой

планеты массы M (см. формулу (2.2) и рис. ниже):

(3.20)

A

=

∫

F ds =

∫

Fdscosα

= R2

− γ Mm dR =

гр

τ

∫

R2

( L)

( L)

R1

R2

dR

1

R2

1

1

= −γMm ∫

= −γMm −

−

R2

= −γMm

,

R

R

R1

R1

R2

1

где α − угол

между направлением

силы и перемещения. Из

рисунка ясно,

что работа сил гравитационного поля при R2 > R1

отрицательна. Это объясняется тем, что гравитационные силы – силы притяжения.

- 66 -

Элементарная длина пути ds=IdrI

2.m

Из формул (3.20) и

(3.17)

следует,

что

.α

потенциальная

энергия

Приращение радиуса dR

гравитационного

поля

m

R2

равна (при R = ∞ Wгр =0):

Fгр

′

1

(3.20 )

Wгр = −γMm R .

Для

потенциальной

1.

энергии тела массы m в

поле

тяготения

Земли,

R1

радиус

которой

27

,

m

M

Rз

формулу

(3.20’)

удобно

К РАСЧЕТУ РАБОТЫ СИЛЫ ГРАВИТАЦИИ.

видоизменить

через

g у поверхности Земли,

ускорение

свободного

падения

и отсчет энергии вести от

поверхности Земли, имея дело с высотой h ( h << Rз):

(3.21)

Wгр

= −γMm 1 = −mg Rз2 = −mg

Rз2

= −mg

Rз

=

R

R

Rз + h

h

1 + Rз

− mgRз + mgh.

Первое слагаемое в правой части (3.21) можно опустить, так

как оно не зависит от положения тела. Справедливо вообще, что

потенциальная энергия системы может быть определена с

точностью до постоянного слагаемого, не влияющего на

изменение энергии.

***** Глава4. §4

*****

§5. Закон сохранения механической энергии

Механической энергией называется энергия механического движения и взаимодействия. Механическая энергия W системы материальных точек равна сумме их кинетической энергии Wk и

потенциальной энергии Wп взаимодействия этих точек друг с

другом и внешними телами28:

(3.22) W =Wk +Wп.

27См. приложение 1 в конце книги

28Внутренние и внешние силы стационарны, то есть не зависят от времени

-67 -

Элементарное приращение механической энергии системы за малый промежуток времени dt :

(3.23) dW = δAнп,

где δAнп − алгебраическая сумма элементарных работ,

совершаемых за время dt всеми действующими на систему внутренними и внешними непотенциальными силами (суммарная работа потенциальных сил равна нулю, см. определения dWk и

dWп).

Если система консервативная, то δAнп ≡ 0 , так как в этом

случае непотенциальных сил нет, а внешние потенциальные силы стационарны, следовательно механическая энергия такой системы

(3.24) W = const .

Формулировка закона сохранения механической энергии:

механическая энергия консервативной системы не изменяется с течением времени.

Закон сохранения механической энергии связан с однородностью времени, то есть с инвариантностью физических законов относительно изменения начала отсчета времени. Это свойство проявляется в том, законы движения любой консервативной системы (тем более замкнутой консервативной системы) не зависят от выбора начала отсчета времени.

Следует заметить, что законы сохранения импульса, момента импульса (см. §7 главы 2) и энергии являются универсальными и применяются не только в классической физике, но и в теории относительности и квантовой физике. Причины этой универсальности были неясны до тех пор, пока не установили их связь со свойствами пространства и времени. Природа законов сохранения в общем виде была вскрыта в 1918 году немецким математиком Эмми Нетер. Согласно теореме Нетер каждому непрерывному преобразованию симметрии физических законов соответствует сохранение определенной физической величины. Наиболее важными примерами подобных преобразований являются параллельный перенос в пространстве (трансляция), сдвиг во времени и поворот в пространстве. Первое из этих преобразований обусловлено однородностью пространства, второе –

-68 -

однородностью времени и третье – изотропией пространства.

Во всех реальных механических системах действуют силы сопротивления и трения, вследствие чего все эти системы неконсервативны. Однако в некоторых случаях их можно приближенно считать консервативными и применять к ним закон сохранения механической энергии. Такой подход возможен, если в рассматриваемом процессе работа всех действующих на систему непотенциальных сил пренебрежимо мала по сравнению с механической энергией системы.

Действие диссипативных сил приводит к постепенному уменьшению механической энергии даже замкнутой системы. Этот процесс называется диссипацией энергии. При диссипации энергии происходит преобразование механической энергии в другие виды энергии (например, в энергию беспорядочного движения молекул). Преобразование механической энергии осуществляется в полном соответствии со всеобщим законом природы – законом сохранении полной энергии.

§6. Применение закона сохранения энергии к космическим скоростям

Аналитическое решение динамической задачи о движении тела в центрально-симметричном гравитационном поле, например, о движении планет вокруг Солнца, сопряжено со значительными математическими трудностями. Между тем применение закона сохранения механической энергии позволяет сравнительно быстро и просто ответить на многие вопросы, касающиеся этого типа движения.

Первую

космическую скорость υ1

(минимальную скорость, которую нужно сообщить

находящемуся на поверхности Земли телу массой m , чтобы оно стало искусственным спутником Земли) наиболее просто можно получить с помощью второго закона Ньютона.

- 69 -

(3.25) marn = F ,

где an −центростремительное ускорение, сообщаемое телу силой тяготения F (см. формулу 2.2 главы 2).

(3.26) m υ12	= mg ,	(3.27) υ	1	=	gR ≈ 7,9 км		,
Rз					з	с

где 29 Rз − радиус Земли.

Определим вторую космическую скорость υ2

(минимальную скорость, которую нужно сообщить находящемуся на поверхности Земли телу, чтобы оно удалилось на бесконечность, то есть освободилось от земного влияния). Проще всего это сделать, используя закон сохранения энергии. Будем считать, что двигатели ракеты срабатывают непосредственно у поверхности Земли, сообщают ракете необходимую скорость υ2 и

выключаются. Механическая энергия тела при запуска в соответствии с формулами (3.11) и (3.21) равна

(3.28) W mυ2 mgRз

= 2 2 − .

Эта энергия в свободном полете в любой момент времени остается неизменной. В конечном состоянии, когда ракета удалилась от Земли на бесконечность, ее потенциальная энергия равна нулю (нет земного влияния). Очевидно также, что искомая начальная скорость будет минимальной, если в конечном состоянии скорость ракеты обратится в нуль. Следовательно, на бесконечности полная механическая энергия равна нулю. Эта энергия равна нулю и на поверхности Земли в соответствии с законом сохранения энергии для консервативной системы телоЗемля:

	(3.29)			mυ22	− mgRз = 0.
				2
Тогда (3.30) υ	2	=	2gR ≈ 11,2 км.
				з	с

29 См. приложение 1 в конце книги

- 70 -