физика механика

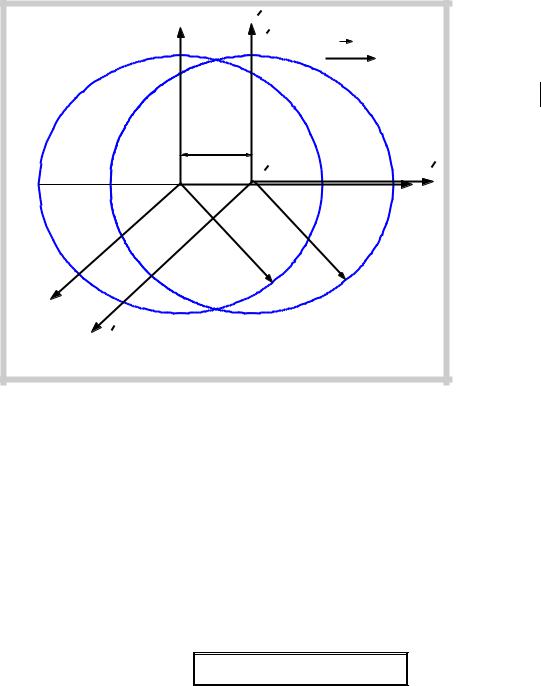
Указанное противоречие можно пояснить на следующем примере (см. рис. ниже). Имеются две инерциальные системы отсчета – неподвижная система Σ и система Σ′, движущаяся вдоль оси ОХ с постоянной скоростью u. Пусть, в момент начала отсчета времени в обеих системах Σ и Σ′ (t = t′ = 0), когда их

начала координат О и O′ совпадают, в точке O производится мгновенная световая вспышка от точечного источника света. К моменту времени t > 0 свет, распространяясь в вакууме со

скоростью c ,	достигнет в системе отсчета Σ точек поверхности
			Σ			сферы		с
	Σ			. u		центром		в
	Y		Y			точке	О	и
						радиусом,
						равным	ct .
						В системе
.A	., O	u*t		.B		Σ′	можно
			O		X	считать,		что
			.		X	световая
			ct			вспышка
				ct		произошла		в
							момент
Z						времени t = 0 в
						точке		O
Z								′
						Поэтому,
РАСПРОСТРАНЕНИЕ СВЕТА ОТ ТОЧЕЧНОГО ИСТОЧНИКА
В ДВУХ ИНЕРЦИАЛЬНЫХ СИСТЕМАХ ОТСЧЕТА						согласно
						постулатам
специальной теории относительности,					к моменту времени			t′ = t

свет в системе Σ′ достигнет точек сферы того же радиуса ct, что и

всистеме Σ, но с центром в точке О′, находящейся в это время не

вточке О, а на расстоянии ut от нее. Таким образом, соединение постулатов специальной теории относительности и классических представлений об абсолютном времени, идущем одинаково во всех системах отсчета, приводит к абсурду – свет вспышки должен одновременно достигать точек пространства, принадлежащих двум разным сферам.

***** Глава4. §2 *****

- 81 -

§3. Одновременность событий. Синхронизация часов

При проведении различных физических измерений широко пользуются понятием одновременности двух или нескольких событий. Например, для определения длины L стержня, расположенного вдоль оси ОХ системы отсчета Σ и движущегося относительно этой системы, необходимо одновременно, т.е. в один и тот же момент времени t , зафиксировать значения х2(t) и

х1	(t) координат концов стержня:
	(4.4) L =		х2(t) − х1(t)		.
	Определение моментов времени совершения того или иного

события (например, старта или посадки космического корабля) сводится к установлению показания часов, одновременного рассматриваемому событию. Это легко сделать с помощью часов, находящихся в том же месте, где происходит событие. Таким образом, в каждой системе отсчета должно быть множество часов, находящихся в различных точках пространства. Само собой разумеется, что все эти часы должны идти согласованно, синхронно – их показания в каждый момент времени t должны быть одинаковыми.

Процедура синхронизации часов, оказывается, является очень не простой задачей. В любом предлагаемом варианте можно всегда найти «слабое» место.

Действительно, синхронность хода часов, находящихся рядом, т.е. в одном и том же месте пространства, можно проверить по совпадению их показаний в каждый произвольный момент времени. Синхронность хода часов, находящихся в удаленных друг от друга точках A и B, можно было бы проверить аналогичным образом, имея возможность посылать сигналы точного времени, распространяющиеся из A и B мгновенно. Однако опыт показывает, что такой способ неосуществим, так как скорость любого сигнала не может превосходить скорости света в вакууме.

Можно поступить следующим образом: перевезти часы из точки B в A , убедиться в синхронности их хода с часами, находящимися в точке A , а затем аккуратно перевезти часы обратно в точку B. Проверить, что привезенные в точку B часы продолжают идти одинаково быстро с часами, оставшимися в точке A , можно с помощью сигналов времени, отправляемых из

- 82 -

Aв B через определенные равные промежутки времени по часам

вточке A . Однако таким способом нельзя установить, не произошел ли при перевозке часов сдвиг в начале отсчета времени по ним, то есть не стали ли часы, привезенные в точку B, спешить

или отставать от часов в точке A на постоянную величину t. Таким образом, вопрос о синхронности хода часов,

находящихся в разных точках A и B, можно решить только путем

однозначного соглашения (определения) относительно того, когда эти часы следует считать синхронными. За основу такого определения Эйнштейн взял реальный физический процесс – распространение света в вакууме. При этом он исходил из того, что скорость света в вакууме, во-первых, является максимально возможной в природе скоростью передачи сигналов, а во-вторых, одинакова во всех направлениях и во всех инерциальных системах отсчета.

Пусть, по часам в точке A световой сигнал отправляется из этой точки в момент времени t1 и после отражения в точке B

возвращается в A в момент времени t3 . Тогда, по определению,

часы в точке B идут синхронно с часами в точке A , если они идут одинаково быстро, и в момент прихода светового сигнала в точку

Bустановленные в ней часы показывают время t2 = (t1 + t3 ) / 2.

Вспециальной теории относительности ход времени в разных инерциальных системах отсчета различен. Соответственно, промежуток времени между какими-либо двумя определенными событиями относителен: он изменяется при переходе от одной инерциальной системы отсчета к другой. В частности, относительна одновременность двух событий, происходящих в разных точках пространства. События,

одновременные в одной инерциальной системе отсчета, вовсе не одновременны в других инерциальных системах отсчета, движущихся относительно первой. В одних системах отсчета первое из этих двух событий происходит раньше второго, а в других – позже второго.

Так, в примере §2 этой главы (см. рис. выше) достижение светом вспышки точек A и B – события, одновременные в

неподвижной системе отсчета Σ. В движущейся системе отсчета Σ′ эти события не одновременны: в точку A , удаляющуюся от точечного источника света – точки O′, свет попадает позже, чем в точку B, приближающуюся к точке O′.

-83 -

События, связанные причинно-следственной связью, не могут совершаться одновременно ни в одной системе отсчета, так как всякое следствие обусловлено каким-то процессом, вызываемым причиной. Между тем любой процесс (физический, химический, биологический) не может протекать мгновенно. Поэтому относительность ни в какой мере не противоречит причинности. В любой инерциальной системе отсчета событиеследствие всегда совершается позже, чем событие, являющееся его причиной.

***** Глава4. §3 *****

§4. Преобразования Лоренца для координат и времени. Преобразования скоростей и ускорений

§4.1. ПреобразованияЛоренцадлякоординативремени

Из постулатов специальной теории относительности, а также из однородности и изотропности пространства и однородности времени следует, что соотношения между координатами и временем одного и того же события в двух инерциальных системах отсчета выражаются преобразованиями Лоренца, а не преобразованиями Галилея, как это считается в классической (ньютоновской) механике. Согласно принципу относительности и вышеуказанным свойствам симметрии пространства и времени преобразования Х. Лоренца (1904г.) должны быть линейными.

Преобразования Лоренца так же, как и преобразования Галилея, имеют простейший вид в том случае, когда сходственные оси декартовых координат неподвижной Σ и движущейся Σ′ инерциальных систем попарно параллельны, причем Σ′ движется относительно Σ с постоянной скоростью u вдоль оси OX (см. рис. в §2 этой главы). Если в качестве начала отсчета времени в обеих системах (t = t′ = 0) выбран тот момент, когда начала координат O и O′ обеих систем совпадают, то преобразования Лоренца для координат и времени имеют вид:

- 84 -

х′ =

х − ut

,

х =

х′ + ut

′

,

1 − u2 / c2

1 − u2 / c2

y′ = y,

y′ = y,

(4.5) z′ =

z,

и (4.6) z′ = z,

ux

ux

′

′

t − c

2

t

+

c2

;

,

t′ =

1 − u2

/ c2

t =

1 − u2 / c2

где с – скорость света в вакууме.

Преобразования Лоренца показывают, что при переходе от одной инерциальной системы отсчета к другой, изменяются не только пространственные координаты рассматриваемых событий, но и соответствующие им моменты времени. Однако между пространственными координатами x′, y′, z′ события и временем t′

его совершения в произвольной инерциальной системе отсчета Σ′ существует определенная взаимосвязь, так что величина

′	=	′	′ 2	′	′ 2	′	′ 2	− c	2	′	′ 2
s12		(x2	− x1 )	+ (y2	− y1 )	+ (z2	− z1 )			(t2	− t1 ) , называемая

интервалом, не зависит от скорости u системы Σ′, то есть одинакова (инвариантна) во всех инерциальных \системах отсчета:

(4.7) s12′ = s12 = inv ,

где индексы 1 и 2 относятся к промежутку времени между рассматриваемыми событиями, измеренными в одной системе отсчета (и время, и расстояние!).

Координата x′ и время t′ не могут быт мнимыми. Поэтому из преобразований Лоренца (4.5) следует, что скорость относительного движения любых двух инерциальных систем отсчета не может превосходить скорости света в вакууме (u ≤ c ).

Согласно первому постулату Эйнштейна физические законы должны удовлетворять условию релятивистской инвариантности. Это означает, что уравнения, выражающие физические законы, должны сохранять свою форму при переходе от одной инерциальной системы отсчета к другой, осуществляемом в соответствии с преобразованиями Лоренца.

Преобразования Лоренца (4.5), (4.6) переходят в преобразования Галилея35 (4.1), (4.1’) при u << c , точнее в пределе

35О преобразовании скоростей и ускорений см. §8 этой главы

-85 -

при uc → 0, то есть при c → ∞. Иными словами, преобразования

Галилея и построенная на них классическая механика построены на предположении о мгновенном распространении взаимодействий. Такой приближенный подход допустим лишь при рассмотрении закономерностей механического движения тел со скоростями, много меньшими скорости света в вакууме.

§4.2. Преобразования скоростейиускоренийврелятивистской кинематике

Пусть, как и прежде (см. рис. в §2 этой главы) сходственные оси декартовых координат систем Σ и Σ′ попарно параллельны и система Σ′ движется относительно Σ с постоянной скоростью ur, направленной вдоль оси OX. Для таких систем, как мы видели, справедливы преобразования Лоренца (4.5), (4.6).

Согласно определению скорости материальной точки ее значения υr и υr′ в двух инерциальных системах отсчета Σ и Σ′ равны:

(4.8)

r

dr

r

r

r

υ =

= i

υx

+

jυy

+ kυz и

dt

(4.9)

r′

=

dr′

r′ ′

r′ ′

r′ ′

′ ,

υ

dt

= i

υx′

+ j υy′

+ k υz

r

r′

где

= i x + jy + kz и

′

′

′

′

′ ′

−

радиусы-векторы

r

r

= i x

+ j y

+ k z

рассматриваемой точки в системах отсчета Σ и Σ′. Проекции

скоростей υ и υ′

на оси декартовых координат равны:

dz′

υ

x

=

dx

, υ

y

=

dy

, υ

z

=

dz

и υ′ ′ =

dx′

, υ′′ =

dy′

, υ′′

=

.

dt

dt

dt′

dt′

dt

x

dt′

y

z

Вычислим, например,

u

2

2

u

d x − ut

1 −

(dx − udt)

1 −

′x′ = dx′

c

2

c2

(4.10) υ

=

=

=

udx

dt′

− ux

1 − u

2

1

−

u2

d t

dt −

2

2

c

2

c

2

c

c

=dx − udt

−udx dt c2

	= dx dt − u		=	υx − u			.
	1 −	u dx	1 −		uυx
		c2 dt			c2

Аналогично можно получить формулы преобразований для двух других проекций скорости:

- 86 -

dy′

υy

1 −

u2

dz′

υz

1 −

u2

(4.11) υ′y′ =

c2

, и (4.12)

υz′′

c2

.

=

=

=

dt′

uυx

dt′

1

−

1

−

uυx

c2

c

2

Для

получения

обратных

преобразований

(υ →υ′)

достаточно

воспользоваться

принципом

относительности

Эйнштейна, не производя каких-либо вычислений:

dx

υ′

′ + u

(4.13)

υx =

=

x

,

dt

uυx′

1 +

c2

dy

υ′y′

1 − u2 c2

(4.14)

υy =

=

,

dt

uυ′x′

1 +

c2

dz

υz′′

1 − u2 c2

(4.15)

υz =

=

.

dt

1 +

uυ′x′

c2

Формулы (4.10)…(4.15) выражают закон сложения скоростей в релятивистской кинематике. В пределе (при c → ∞)

они приводят к обычному галилеевскому закону сложения скоростей (4.1), (4.1’).

Из соотношений (4.10)-(4.15) видно, что частица, движущаяся относительно какой-либо инерциальной системы отсчета со скоростью, меньшей c , имеет скорость относительно любой другой инерциальной системы отсчета также меньшую скорости света в вакууме. Отсюда, в частности, следует, что как бы ни были близки к c скорости двух частиц, их относительная скорость всегда меньше c .

Пример 1. Две частицы движутся вдоль оси ОХ системы отсчета Σ навстречуr друг другу со скоростями, соответственно

равными: υr1 = 0,8ci , υr2 = −0,8ci ( i − единичный орт оси ОХ). Вычислить относительную скорость u21 движения частиц.

a Искомая скорость равна скорости второй частицы относительно системы отсчета Σ′, движущейся вместе с первой

- 87 -

частицей ( ur =υr1 = 0,8ci ),

то

есть

u21 =υ2′ .

Из формулы (4.10)

следует, что

υ2 x − u

1,6c

υ2′ x′ =

= −

= −0,976c,

υ2′ y′ =υ2′z′ = 0.

1

+ 0,64

1 −

uυ2 x

c2

ur21 = −0,976ci ,

ur21

< c .

Таким образом,

Используя прежние обозначения и аналогичный подход, примененный нами при вычислении проекции скорости υx в

формуле (4.10), а затем принцип относительности Эйнштейна, можно получить соответствующие проекции ускорений в прямых (a′ → a ) и обратных преобразованиях (a → a′).

Вычислим, например,

(4.16) a′x′ =

=

υx − u

d

1

−

uυx

dυ′x′

c2

=

=

dt′

ux

u

2

d

t −

1

−

c2

c2

dx − udt		= dx dt − u		= υx − u
	udx		u dx
dt −		1 −		1 −		uυx
	c2		c2 dt			c2

(dx − udt)

1 −

u2

c2

=

udx

1

−

u2

dt −

c2

c2

u

2

3

1 −

c

2

= ax

.

uυ

x

1 −

c2

Выполняя аналогичные, но более громоздкие преобразования, получим:

dυ′

uυx

uυ

1 −

u2

y

c

2

(4.17)

′

y′

1

−

2

3 ,

ay′ =

dt′

=

c

2

ay +

c

ax

uυ

x

1

−

c2

- 88 -

dυ′

uυ

uυ

1 −

u2

(4.18) a′z′ =

′

x

z

c

2

z

= 1

−

az +

ax

.

dt′

c2

uυ

3

c2

x

1

−

c2

Обратные преобразования получим, поменяв на противоположные знаки соответствующих проекций скоростей и поставив штрихи у проекций ускорений, скоростей, координат в правой части формул (4.16…4.18):

(4.19)

(4.20)

(4.21)

u

2

3

1 −

a

=

dυx

= a′ ′

c2

,

x

dt

uυ′x′

x

1 +

c2

dυy

uυ′

′

uυ′y′

ay =

x

′

′

1 +

dt

=

c

2

ay′ −

c

2 ax′

	dυ	z			uυ′		uυ′	′
az =			= 1	+	x′	a′z′ −	z		a′x′
	dt				c2		c2

***** Глава4. §4 *****

1

−

u2

c

2

3 ,

uυ

′

′

1

+

x

c2

1

−

u2

c2

.

uυ′

′ 3

1

+

x

c2

		§5. Лоренцево сокращение длины
	Пусть,		L0 −		длина	Y Σ		Y' Σ
стержня,			покоящегося		в
движущейся			системе	отсчета						u
Σ′.	При		этом	стержень						стержень
расположен вдоль оси					′ ′
					O X ,
следовательно, L0 = x2′				− x1′, где			.	0'.	x'	x'
x2′ , x1′ −		координаты		концов
									1	2 X'
стержня (см. рис.).						0			x1(t)	x2(t) X
						Измерение длины стержня в двух
	Длина L того же стержня					инерциальных системах отсчета
в	системе		отсчета		Σ,
				- 89 -

относительно которой он движется со скоростью u, равна разности значений координат концов стержня, измеренных в один и тот же момент времени t :

(4.22)

′

′

(t)) 1

− u

2

c

2

= L0

1 − u

2

c

2

.

L = x2(t) − x1(t) = (x2

(t) − x1

Поперечные размеры тела не зависят от скорости его движения и одинаковы во всех инерциальных системах отсчета:

(4.23) y2 − y1 = y2′ − y1′ и z2 − z1 = z′2 − z1′ .

Таким образом, линейные размеры тела относительны. Они максимальны в той инерциальной системе отсчета, относительно которой тело покоится. Эти размеры тела называются собственными. Линейный размер тела уменьшается в направлении движения с точки зрения наблюдателя, находящегося в покоящейся системе отсчета, относительно которой движется тело.

Лоренцево сокращение является кинематическим эффектом специальной теории относительности. Оно не связано с действием на движущееся тело каких-либо продольных сил, сжимающих тело при скоростях движения, близких к скорости света в вакууме. Из (4.8) следует, что тела не могут двигаться со скоростями u ≥ c , так как при u = c продольный размер тела обращается в нуль, а при u > c он становится мнимым.

***** Глава4. §5 *****

§6. Лоренцево замедление времени. Интервал между двумя событиями

§6.1. Лоренцево замедление времени

Пусть, в движущейся инерциальной системе отсчета Σ′ два рассматриваемых события 1 и 2 происходят в одной и той же неподвижной относительно Σ′ точке A (x2′ = x1′) в моменты

времени t1′ и t2′ , так что промежуток времени между этими

событиями τ0 = t2′ − t1′.

Относительно неподвижной инерциальной системы Σ точка A движется с той же скоростью u , что и система Σ′. Поэтому события 1 и 2 совершаются в разных точках пространства с координатами x1 и x2 , причем x2 − x1 = uτ , где τ = t2 − t1 −

- 90 -