
- •Е.А. Калиберда е.П. Яхина анализ эффективности информационных систем
- •Предисловие
- •Введение
- •Экономические методы оценки эффективности ис
- •1.1. Финансовые методы оценки эффективности
- •Статические методы оценки Метод окупаемости
- •Метод «затраты - прибыль»
- •Динамические методы оценки Метод чистой текущей стоимости (npv)
- •Метод индекса рентабельности (pi)
- •Метод внутренней нормы доходности (irr)
- •1.2. Затратные методы оценки эффективности ис
- •Совокупная стоимость владения
- •Невидимые затраты
- •Неконтролируемые затраты
- •Первоначальные затраты
- •1.3. Комплексные методы оценки эффективности ис Система сбалансированных показателей (Balanced Scorecard)
- •1.4. Пример расчета затрат на информационную систему
- •2. Элементы теории вероятности
- •2.1. Формулы комбинаторики
- •2.2. Случайная величина
- •Свойства математического ожидания
- •Математическое ожидание числа появления события в независимых испытаниях
- •2.3. Биноминальное распределение
- •2.4. Распределение Пуассона
- •2.5. Экспоненциальное распределение
- •2.6. Простейший поток событий
- •3. Качество и эффективность информационных систем Методы оценки качества
- •3.1. Показатели качества программного изделия
- •Количественные показатели функциональных возможностей программного изделия
- •Количественные показатели эффективности программного изделия
- •Количественная оценка безопасности информационной системы
- •3. 2. Основные понятия теории надёжности
- •Определение надёжности программного изделия
- •Основные количественные показатели надёжности
- •3.3. Примеры оценки основных показателей качества
- •4. Тестировапние программных проодуктов Понятие тестирования
- •Роль тестирования в процессе разработки программ
- •4.1. Различные подходы к тестированию (черный ящик, белый ящик)
- •4.2. Смежные вопросы тестирования
- •Заключение
- •Библиографический список
- •ПриложенИя
- •Работы, выполняемые разработчиками постановки задачи
- •Работы, выполняемые разработчиками постановки задачи
- •Работы, выполняемые разработчиками постановки задачи
Свойства математического ожидания
1. Математическое ожидание постоянной величины равно самой постоянной
![]() (2.10)
(2.10)
2. Постоянный множитель можно вынести за знак математического ожидания:
![]() (2.11)
(2.11)
3. Математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий.
![]() (2.12)
(2.12)
Пример 3
Независимые случайные величины Х и У заданы следующими законами распределения:
Х 5 2 3 У 7 9
Р 0.6 0.1 0.3 р 0.8 0.2
Найти математическое ожидание величины ХУ.
Решение:
Найдём математическое ожидание каждой из данных величин:
![]()
![]()
![]()
Математическое ожидание числа появления события в независимых испытаниях
Пусть производится n независимых испытаний в каждом из которых вероятность появления события А постоянна и равна p. Чему равно среднее число появлений события А в этих испытаниях?
Теорема
Математическое ожидание М(Х) числа появления события А в n независимых испытаниях равно произведению числа испытаний на вероятность появления события в каждом испытании:
![]() .
(2.13)
.
(2.13)
Пример 4
Вероятность
попадания в цель при стрельбе из орудия
![]() .
Найти математическое ожидание общего
числа попаданий, если будет произведено
10 выстрелов.
.
Найти математическое ожидание общего
числа попаданий, если будет произведено
10 выстрелов.
Попадание при каждом выстреле не зависит от исходов других выстрелов, поэтому рассматриваемые события независимы и, следовательно, искомое математическое ожидание
![]() .
.
Если
![]() - случайная величина, то функция
- случайная величина, то функция
![]() (2.14)
(2.14)
называется функцией
распределения
случайной
величины
![]() .
Здесь -
.
Здесь -![]() - вероятность того, что случайная величина
- вероятность того, что случайная величина![]() принимает значения, не превосходящие
числа
принимает значения, не превосходящие
числа![]() .
.
Функция распределения любой случайной величины обладает следующими свойствами:
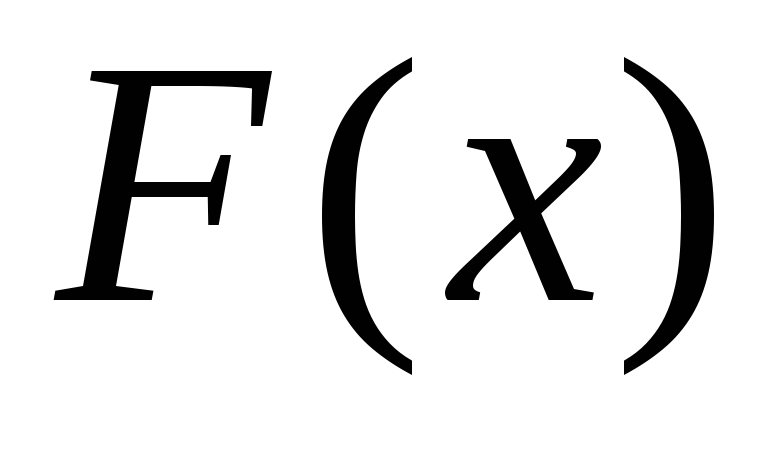 определена
на всей числовой прямой R;
определена
на всей числовой прямой R;
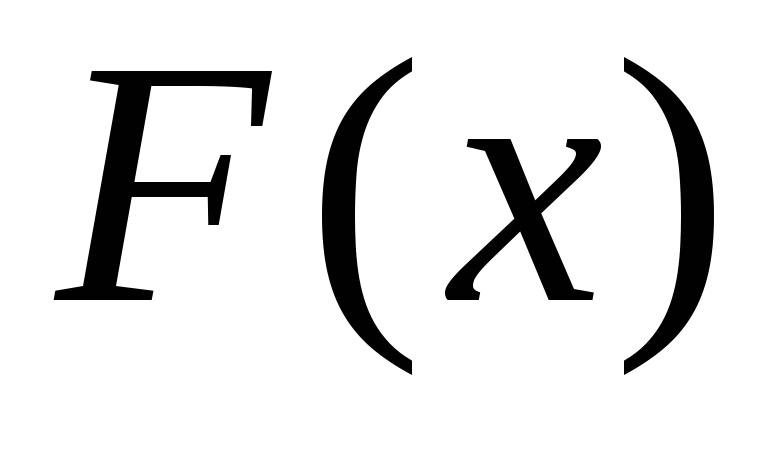 не убывает, т.е.
если
не убывает, т.е.
если ,
то
,
то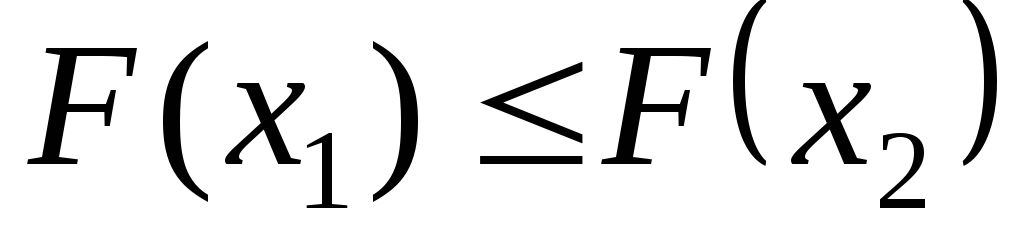 ;
; ,
,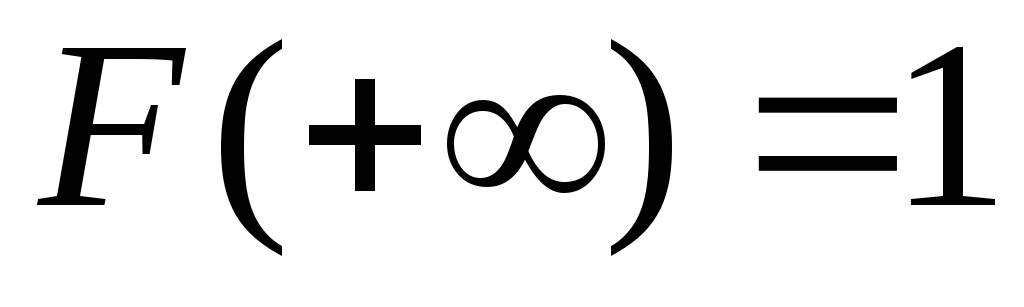 ,т.е.
,т.е.
 и
и
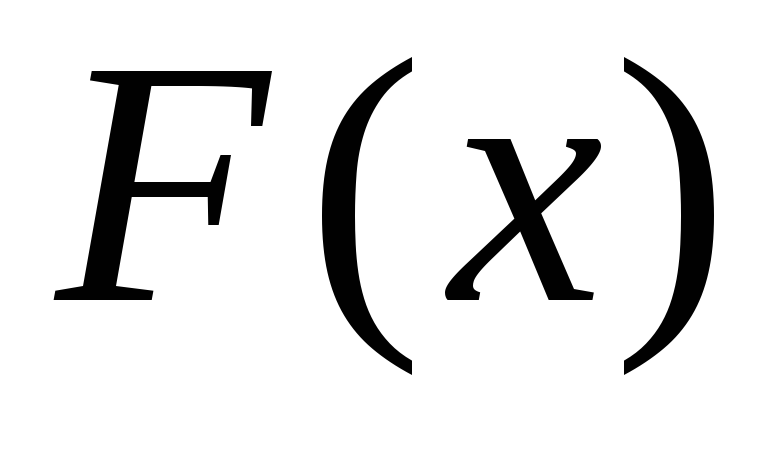 непрерывна справа,
т.е.
непрерывна справа,
т.е.

Функция распределения содержит всю информация об этой случайной величине и поэтому изучение случайной величины заключается в исследовании ее функции распределения, которую часто называют просто распределением. Так что, когда говорят о нормальном распределении, то подразумевают случайную величину, имеющую нормальную функцию распределения.
У дискретной случайной величины функция распределения ступенчатая.
Пример 5
Случайная величина принимает значение числа очков, выпавшее при однократном бросании кости. Определим ее функцию распределения :
Если
![]() -
дискретная случайная величина, принимающая
значения
-
дискретная случайная величина, принимающая
значения![]() с
вероятностями
с
вероятностями![]() ,
то таблица вида
,
то таблица вида
|
|
|
|
... |
|
... |
|
|
|
|
... |
|
... |
называется распределением дискретной случайной величины.
Вероятность того,
что значение случайной величины
![]() попадает в интервал
попадает в интервал![]() вычисляется для дискретной случайной
величины по формуле:
вычисляется для дискретной случайной
величины по формуле:
![]() (2.15)
(2.15)
2.3. Биноминальное распределение
Пусть производится
n
независимых испытаний, в каждом из
которых событие А
может появиться либо не появиться.
Вероятность наступления события во
всех испытаниях постоянна и равна p
(следовательно,
вероятность непоявления
![]() ).
Рассмотрим в качестве дискретной
случайной величиныХ
число
появлений события А
в этих испытаниях.
).
Рассмотрим в качестве дискретной
случайной величиныХ
число
появлений события А
в этих испытаниях.
Поставим перед
собой задачу: найти закон распределения
величины Х.
Для её решения требуется определить
возможные значения Х
и их
вероятности. Очевидно, событие А
в n
испытаниях либо появится 1 раз, либо 2
раза, …, либо n
раз. Таким образом, возможные значения
Х таковы:
![]() .
Остаётся найти вероятности этих возможных
значений, для чего достаточно
воспользоваться формулой Бернулли:
.
Остаётся найти вероятности этих возможных
значений, для чего достаточно
воспользоваться формулой Бернулли:
![]() ,
(2.16)
,
(2.16)
где k=0, 1, 2, …, n.
Данная формула и является аналитическим выражением искомого закона распределения.
Распределение, определяемое формулой Бернулли называют биноминальным. Потому что правую часть равенства можно рассматривать как общий член разложения бинома Ньютона.
![]() .
(2.17)
.
(2.17)
Таким образом,
первый член разложения
![]() определяет вероятность наступления
рассматриваемого события n раз в n
независимых испытаниях; второй член
определяет вероятность наступления
рассматриваемого события n раз в n
независимых испытаниях; второй член![]() определяет вероятность наступления
события
определяет вероятность наступления
события![]() раз; …; последний член
раз; …; последний член![]() определяет вероятность того, что событие
не появится ни разу.
определяет вероятность того, что событие
не появится ни разу.
Напишем биноминальный закон в виде таблицы:
X n n-1 … k … 0
Р
![]()
![]() …
…![]() …
…![]()
Математическое ожидание для биноминального распределения имеет вид:
![]() ,
(2.18)
,
(2.18)
Пример 6
Монета брошена 2 раза. Написать в виде таблицы закон распределения случайной величины Х – числа выпадений «герба».
Решение:
Вероятность
появления герба в каждом бросании монеты
![]() ,
следовательно вероятность непоявления
герба
,
следовательно вероятность непоявления
герба![]() .
.
При бросании монеты
«герб» может появиться либо 2 раза, либо
1 раз, либо совсем не появиться. Таким
образом, возможные значения Х таковы:
![]() .
Найдём вероятности этих возможных
значений по формуле Бернулли:
.
Найдём вероятности этих возможных
значений по формуле Бернулли:
![]()
![]()
![]()
Напишем искомый закон распределения:
Х 2 1 0
Р 0.25 0.5 0.25.
