gos / Гетманов3

			k /2	j Ts	e	j Ts
	H ( j T ) e j Tk /2		2h(s) e
		h(0)
			s 1		2

	k /2
e j Tk /2 h(0) 2h(s) cos( Ts) ,
	s 1

и во втором случае ПФ КИХ-фильтра имеет вид

	k /2
H ( j T ) e j Tk /2 h(0) 2 jh(s)
	s 1
	k /2
e j /2 j Tk /2 h(0) 2h(s)
	s 1

e j Ts e j Ts
2 j

sin( Ts) .

Усечение ряда (6.5.10) и формирование ПФ (6.5.12) приводит к эффекту Гиббса, связанному с образованием пульсаций АЧХ около её точки разрыва (точки среза). Использование весовой последовательности конечной длины w(s), s 0, 1,..., k, которая называется

оконной функцией, для умножения коэффициентов Фурье с целью регулирования сходимости усечённого ряда Фурье даёт хорошие результаты в отношении устранения эффекта Гиббса.

Пусть H0 (e j T ) – частотная функция неусечённого ЦФ из (6.5.10). Положим, что для выбранной оконной функции w(s) найдена частотная функция

	k /2
W (e j T ) W (z) Z{w(s)}	w(s)z s .
	s k /2

Обозначим через Hw (z) Z{w(s)h(s)} частотную функцию КИХ-

фильтра, полученного в результате умножения коэффициентов им- пульсно-переходной функции на функцию окна. Произведение функций во временной области переводится в свёртку в частотной области. Тогда очевидна запись в виде свёртки

		T	2 /T
	Hw (e j T )			H (e j 1T )W (e j( 1)T )d 1.
		2
			0

Частотная функция окна W (e j T ) должна иметь главный лепесток,

содержащий почти всю энергию окна, и боковые лепестки, которые должны обычно быстро затухать. При определённом выборе функции окна w(s) удаётся устранить явление Гиббса. Наиболее часто

216

для рассматриваемой здесь задачи используются временные оконные функции Хэннинга, Хемминга и Блэкмана. Разумеется, существует целый ряд других функций окон.

Рассмотрим пример синтеза низкочастотного КИХ-фильтра с заданными c , T и заданной эталонной функцией АЧХ

H0 ( j T ) в виде

	H0 ( j T )			1 при 0 c ;
				при c 2 / 2T.
H0 ( j T )		0

Будем полагать, что для эталонной ПФ справедливо равенство

H0 ( j T ) 1 для 0 c , H0 ( j T ) 0 для	c 2 / 2T и
H0 ( j T ) имеет период 2 / 2T.

Найдём импульсно-переходную характеристику предполагаемого к синтезу КИХ-фильтра на основе разложения в ряд Фурье

H0 ( j T ), вычислим интеграл в симметричных пределах:

T

2 /T

T

/T

h(s)

H0 ( j T )e j Tsd

H0 ( j T )e j Ts d

2

2

0

/T

T

c

1 e j Ts d

T e j Ts

c

2

2 ( jTs)

c

c

T (e j cTs e j cs )

sin( Ts)

c

.

2 ( jTs)

s

Запишем выражение для ПФ физически реализуемого КИХфильтра для z-переменных, пусть k – чётное число:

	k /2
H (z) z k /2 h(0) h(s)(zs z s ) ,
	s 1

	где a0 h(0)	cT	,	as	2h(s)	2sin( cTs)	, s 1,..., k 2.
						s

ПФ синтезированного КИХ-фильтра имеет вид

k /2

H ( j T ) e j Tk /2 as (e j Ts e j Ts ) s 0

217

		k /2
e j Tk /2 as cos( Ts).							(6.5.13)
		s 0
КИХ-фильтр (6.5.13)		синтезирован с прямоугольным окном
w0 (s) 1 при 0 s k,	w0 (s) 0			при s 0, s k . На рис. 6.5.1а,
6.5.1б изображены АЧХ		H ( j T )		и L		H ( j T )		синтезированного

КИХ-фильтра (6.5.13) для k 100, c 8, T 0,2 в линейном и логарифмическом масштабе. Видно, что в окрестности частоты среза с функция АЧХ имеет значительные пульсации в полосе пропускания и задерживания.

Рис. 6.5.1а. АЧХ синтезированного КИХ-фильтра с прямоугольным окном в линейном масштабе

Рис. 6.5.1б. АЧХ синтезированного КИХ-фильтра с прямоугольным окном в логарифмическом масштабе

218

Этот же пример рассмотрим, когда для синтеза КИХ-фильтра используется окно Хэннинга. Для этого последовательность коэффициентов as умножается на функцию wH (s), которая описывает-

ся весовой функцией
w (s) 0,5 0,5сos 2 s		при 0 s k,	w (s) 0	при s 0,	s k.
H	k		H

Модифицированная ПФ для синтезированного фильтра представляется формулой

k /2
H ( j T ) e j Tk /2 as wH (s)cos( Ts).	(6.5.14)

s 0

На рис. 6.5.2а, 6.5.2б изображены АЧХ H ( j T ) синтезированного

КИХ-фильтра с окном Хэннинга в линейном и логарифмическом масштабе. Видно, что благодаря применению окна существенно снижаются пульсации в полосе пропускания и уровень пульсаций в полосе задержания снижается почти до 50 Дб.

Рис. 6.5.2а. АЧХ синтезированного КИХ-фильтра с окном Хэннинга в линейном масштабе

219

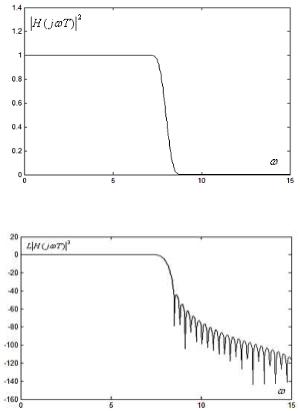
Рис. 6.5.2б. АЧХ синтезированного КИХ-фильтра с окном Хэннинга в логарифмическом масштабе

Рис. 6.5.3а. АЧХ синтезированного КИХ-фильтра с окном Блэкмана в линейном масштабе

Рис. 6.5.3б. АЧХ синтезированного КИХ-фильтра с окном Блэкмана в логарифмическом масштабе

Рассмотрим пример синтеза КИХ-фильтра с использованием окна Блэкманна

w (s) 0,42 0,5сos 2 s 0,08cos 4 s				при 0 s k,
B	k	k
	wH (s) 0	при s 0,	s k.

ПФ для синтезированного КИХ-фильтра с wB (s) представляется формулой

220

k /2
H ( j T ) e j Tk /2 as wB (s) cos( Ts) .	(6.5.15)

s 0

Из рис. 6.5.3а и 6.5.3б видно, что в результате применения окна Блэкмана практически полностью устраняются пульсации в полосе пропускания и уровень пульсаций в полосе задерживания снижается до 80 Дб.

6.5.4. Синтез КИХ-фильтров методом частотных выборок

Продолжим рассмотрение задачи построения КИХ-фильтров в частотной области. Передаточная функция КИХ-фильтров внешне напоминает дискретное преобразование Фурье. Воспользуемся этим обстоятельством при решении задачи синтеза. Действительно, запишем снова выражение ПФ

k

H (a, j T ) ase j Ts .

s 0

Расположим частотные точки равномерно r ; r 0, 1,..., k;r r; 2 /(k 1). Пусть комплексные значения H0 ( j rT )

задают эталонную ПФ для КИХ-фильтра в равномерно расположенных дискретных частотных точках. Введём нормированные частотные выборки H0,r H0 ( j rT )/(k 1). Очевидно, что после-

довательности частотных выборок H0,r и коэффициенты as связаны прямым и обратным дискретным преобразованием Фурье:

k

2

H0,r

1

ase j

rs ,

r 0, 1,..., k,

k 1

k 1

s 0

k

j

2 rs

k

H

( j T )

j

2

rs

0

as H0,r e

N

r

e

k 1

,

s 0, 1,..., k.

k 1

r 0

r 0

На практике решение задачи синтеза КИХ-фильтров практически всегда связано с тем, что требуется синтезировать АЧХ заданного вида с помощью КИХ-фильтра с действительными коэффициентами as . Воспользуемся подходом разд. 6.5.2, основанным на формировании КИХ-фильтров с линейными ФЧХ.

221

Рассмотрим пример задачи синтеза с k-нечётным. Сформируем

симметричную АЧХ Hr ,	r 0,..., k,	Hr Hk 1 r ,	которая соот-
ветствует в точках r 0,	1,..., (k 1) / 2 значениям		заданной эта-

лонной Hr H0,r . Тогда коэффициенты КИХ-фильтра представятся следующей формулой:

k	j	2	rs		(k 1)/2		2
as Hr e		k 1				2Hr cos		rs ,
							k 1
r 0					r 0
s 0,..., (k 1)/2,						as ak 1 s .

Нетрудно видеть, что симметричные коэффициенты as являются действительными.

6.5.5.Синтез КИХ-фильтров по методу аппроксимации во временной области

Данный метод синтеза основан на решении задачи аппроксимации во временной области наблюдений сигнала на ограниченном числе дискретных точек с помощью линейной по параметрам модели. Рассмотрим с учётом определённых допущений используемую здесь задачу аппроксимации и предлагаемый алгоритм синтеза.

Пусть задана выборка из (k 1) наблюдений сигнала y(s) y(Ts), s 0, 1,..., k. Аппроксимируем указанные наблюдения линейной по параметрам c1, c2 ,..., cm моделью в виде полиномиальной функции

m

yM (c,Ts) cr (Ts)r 1.

r 1

Cформируем квадратичный функционал

k		m
S(c, y) y(s) cr (Ts)
s 0		r 1

r 1 2 .

Решение задачи аппроксимации связано с вычислением оптималь-

ного вектора параметров c модели, который обеспечивает минимальное значение функционала, физический смысл которого очевиден. С помощью векторно-матричных обозначений вектора на-

222

блюдений Y и матрицы X

0

оптимальный вектор параметров c

находится следующим образом:

y(0)

1

T 0

(T 0)m 1

Y

y(1)

,

X

0

1

T 1

(T 1)m 1

,

c (X T X

0

) 1 X T Y.

0

0

y(k)

1

T k

(T k)m 1

Для того, чтобы избежать проблем с вычислениями, будем полагать, что k, m принимают малые значения.

Введём матрицу D размерности (m, k 1) и представим вектор c в виде линейной функции от вектора наблюдений

		k
D (X0T X0 ) 1 X0T ,	c DY ,	cr drs y(s),	r 1,..., m,	(6.5.16)
		s 0
где drs , r 1,..., m,	s 0, 1,...,	k, – коэффициенты матрицы D. Мо-
дель сигнала для	вектора параметров c в		некоторой	точке i,

0 i k, может быть найдена в виде линейной комбинации наблюдений

m	m		k
yM (c , Ti) cr (Ti)r 1			drs y(s)		(Ti)r 1
r 1	r 1	s 0

k	m
	drs (Ti)r 1	y(s).
s 0	r 1

Точка i в общем случае не связана со значением k; рассмотрим ча-

стный случай i k. Введём коэффициенты		ak s ,	s 0, 1,..., k, и
представим значение модели сигнала в точке k в виде свёртки
m		k
drs (Tk)r 1 ak s ,	yM (c , Tk)	ak s y(s).		(6.5.17)
r 1		s 0

Примем yM (c , Tk) в качестве результата фильтрации наблюдений y(0), y(1),..., y(k) для точки k, введём обозначение x(k) :

	k	k
yM (c , Tk) x(k) ,	x(k) ak s y(s) as y(k s). (6.5.18)
	s 0	s 0

Основываясь на выражении (6.5.18), можно сформировать КИХфильтр. Положим, что последовательность наблюдений сигнала

223

y(i) реализована для k i . Результат фильтрации сигнала x(i) в точке i, полученный на основе скользящего усреднения наблюдений y(i), y(i 1),..., y(i k) для 0 i , представляется соотношением

k
x(i) as y(i s),	i 0, 1, 2,.. .	(6.5.19)
s 0

Алгоритм синтеза КИХ-фильтра во временной области базируется на соотношении (6.5.16), которое позволяет вычислить по T, k, m коэффициенты drs матрицы D, и соотношении (6.5.17), на

основе которого может быть вычислен вектор as (или ak s ). Разберём пример синтеза КИХ-фильтра во временной области

по трём наблюдениям y(0), y(1), y(2),			которые соответствуют
k 2.	В качестве аппроксимационной модели выбираем прямую
линию	yM (c, Ts) c1 c2Ts,	s 0, 1, 2.	Введём векторно-матрич-

ные обозначения Y , X0 и произведём необходимые вычисления, положив T 1. Опустив промежуточные выкладки, получим

	y(0)				1	0					5	1	1
													6
Y	y(1)	, X	0		1	T	, D (X T X		0	) 1 X T	6	3		.
							0			0	1		1
	y(2)				1	2T						0
Оптимальные коэффициенты модели примут вид											2		2
	с 5 y(0) 1 y(1) 1 y(2),							c		1 y(0) 1 y(2).
1		6		3		6		2		2	2

Значение модели в точке s 2 представится следующим образом: x(2) yM (c , 2) c1 2c2 16 y(0) 13 y(1) 56 y(2). (6.5.20)

Уравнение КИХ-фильтра, реализующего скользящее усреднение, и его коэффициенты запишутся на основании (6.1.20):

x(i) 56 y(i) 13 y(i 1) 16 y(i 2), a0 56 , a1 13 , a2 16 . (6.5.21)

На рис. 6.5.4 представлены результаты математического моделирования работы КИХ-фильтра, синтезированного по предлагае-

224

мому алгоритму.		Модельные	зашумленные	наблюдения
y(i) y(Ti)	с i 0, 1,..., N 1 формируются по формуле
	y(i) y	(i) w(i), y	(i) 1 e T (i 1) ,	(6.5.22)
	0	0

где w(i) – модельные случайные нормальные числа с нулевым ма-

тематическим ожиданием и дисперсией 2. Для (6.5.22) приняты численные значения параметров 0,1; T 1; N 35; 0,1. В качестве модельной функции, реализующей аппроксимацию наблюдений, взята прямая yM (c, Ts) c1 c2Тs, s 0, 1,..., k, k 5. Уравнение КИХ-фильтра представится следующей формулой:

5

x(i) as y(i s),

s 0

где a0 0,5238; a1 0,3810; a2 0,2381; a3 0,0952; a4 0,0476; a5 0,1905 – значения его вычисленных по (6.5.16) и (6.5.17) ко-

эффициентов.

Пунктирная кривая 1 относится к исходному экспоненциальному сигналу y0 (i), ломаная линия 2 с крестиками соответствует зашумлённым наблюдениям y(i), ломаная линия с кружочками обозначает выходной сигнал фильтра x(i). Вычисления x(i) реализованы для точек k i N; на кривой 3 принято x(i) y0 (i) для

0 i k 1. Анализ кривых на рис. 6.5.4 позволяет сделать вывод, что описанный метод синтеза КИХ-фильтров на основе аппроксимации во временной области является вполне работоспособным.

225