Двойное векторное произведение

Двойное векторное произведение есть тернарная операция, результатом применения которой к трем векторам является снова вектор. Эта операция часто встречается в механике. Выражение называется двойным векторным произведением векторов .

Двойное векторное произведение выражается через скалярное произведение. Имеет место следующее

Предложение (тождество “бац минус цаб”).

.

Инвариантные, т.е. не связанные с выбором базиса, доказательства этого тождества требуют несколько виртуозных геометрических построений в пространстве. В правом ортонормированном базисе доказательство представляет собой простую проверку и предлагается в качестве упражнения ниже.

Оказывается, векторное произведение не ассоциативно, т.е. существуют векторы такие, что. В то же время векторное произведение удовлетворяет важнейшемутождеству Ли-Якоби:

.

Его легко доказать (докажите!), опираясь на предыдущее предложение. С помощью тождества "бац минус цаб" легко вычисляется также скалярное произведение

двух векторных произведений. Делая в тождестве

замену , получим

.

Применим здесь к тождество "бац минус цаб":

,

т.е.

. (2.17)

Применив тождество "бац минус цаб" к векторному произведению двух векторных произведений, получим

.

Выведем полезное тождество

. (2.18)

Из тождества "бац минус цаб" следует

,(2.19)

что и требовалось доказать.

Теперь рассмотрим последовательное векторное произведение

.

Распишем по тождеству "бац минус цаб". Отсюда

. (2.20)

В приложениях бывает необходимо разложить вектор a по единичному вектору и ему перпендикулярному .

Тождество "бац минус цаб" дает

.

Отсюда

. (2.21)

Решение векторных уравнений

В векторных уравнениях искомой величиной является вектор. Векторное уравнение или система таковых может иметь единственное решение, бесконечно много решений или не иметь их вовсе.

Рассмотрим некоторые важные уравнения.

1. Рассмотрим на плоскости систему

(2.22)

(векторы a и b неколлинеарны). Она равносильна системе

которая единственным образом определяет вектор x его ортогональными проекциями ина оси базисных векторов(рис. 7).

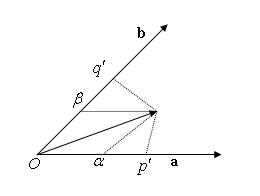
Рис. 7. Ковариантные координаты

Отметим, что числа ,называют ковариантными координатами вектораx в базисе , . Если , то ковариантные координаты вектора совпадают с его ортогональными проекциями на базисные вектора. Обычные координаты вектораx называют контравариантными. При этом (рис. 7)

.

Если базис ортонормированный, то ковариантные координаты вектора совпадают с его контравариантными координатами.

2. При рассмотрим систему

(2.23)

Тройка векторов образует базис. Разложим векторx по этому базису:

.

Тогда

.

Учитывая тождество "бац минус цаб", получим

.

Отсюда

, , ,

и система имеет решение лишь при . Первое уравнение теперь примет вид

.

Отсюда . Таким образом, при система (2.23) имеет единственное решение

.

3. При рассмотрим уравнение

.

Умножим его векторное справа на b:

.

Полученное уравнение умножим скалярно на c:

.

Отсюда

.

Аналогично

, .

Отметим, что решение определяет координаты вектора d в базисе как отношение соответствующих объемов.

4. При рассмотрим систему

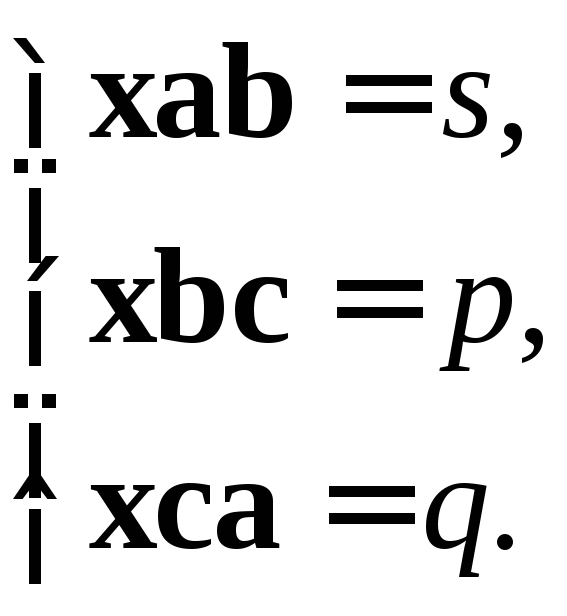(2.24)

Вектор x будем искать в виде . Тогда первое уравнение примет вид

.

Отсюда . Аналогично из второго и третьего уравнений найдем и. Окончательно

.

5. Покажем, что решение системы векторных уравнений

(2.25)

где – данные векторы, а – искомый вектор, приможно записать в форме

.

Так как , то тройка векторов,,образует базис. Будем искать решение в виде

.

Из первого уравнения имеем

, .

Аналогично находятся ,. Окончательно

.

Упражнение 1. Объяснить геометрический смысл решения системы

(2.26)

в пространстве (векторы некомпланарные).

Упражнение 2. Показать, что при уравнение

имеет решение

; ; .
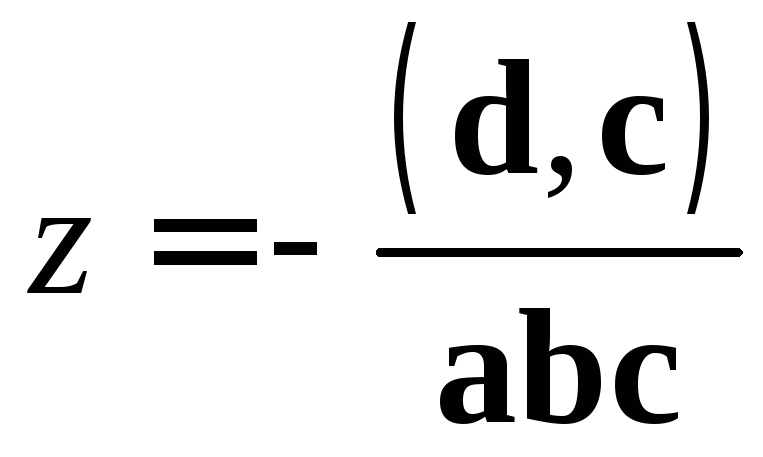