Лекция 17. Ряд Фурье по тригонометрической системе функций (тригонометрический ряд Фурье)

Тригонометрической системой функций называется система функций

Это – периодические функции.

Докажем два свойства периодических функций.

1. Если функция имеет период ,то функция имеет период.

Доказательство. .

2. Если функция имеет период , то .

Доказательство. =

(делаем замену переменных в последнем интеграле )

.

Доказанные свойства позволяют

1. рассматривать тригонометрическую систему функций на любом отрезке длиной (периодравен,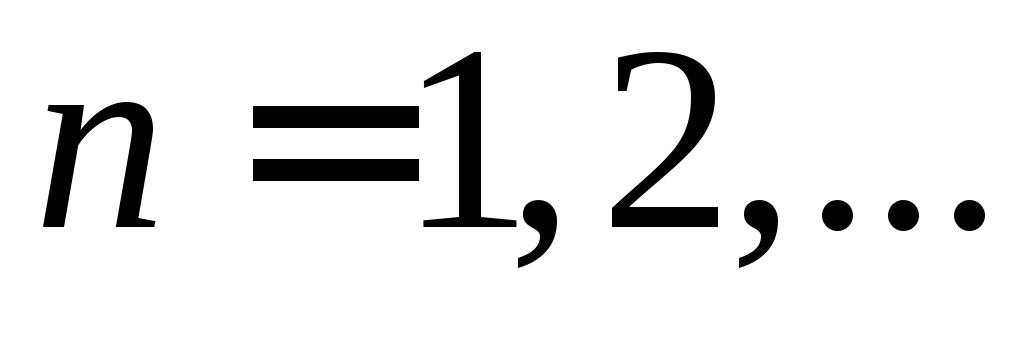), напримерна отрезке ,

2. при вычислениях интегралов от функций с периодом, кратным , проводить интегрирование по любому отрезку длиной.

Так как элементы тригонометрической системы функций представляют собой непрерывные функции, то они сами и их квадраты (как произведение непрерывных функций) интегрируемы на отрезке . Поэтому можно рассматривать пространство L² на отрезке и строить ряд Фурье.

Скалярное произведение функций введем так:

Для того, чтобы построить ряд Фурье по тригонометрической системе функций надо доказать, что эти функции попарно ортогональны на .

Теорема. Тригонометрическая система функций состоит из попарно ортогональных на отрезке функций.

Доказательство. .,

,

Пусть .

Теорема доказана.

Вычислим скалярные квадраты элементов тригонометрической системы.

,

.

Составим ряд Фурье по тригонометрической системе функций

.

Коэффициенты Фурье вычисляются по формуле .

,

,

.

Теперь необходимо сформулировать условия, при которых функция представляется рядом Фурье по тригонометрической системе функций.

Условия Дирихле.

1. Интервал, на котором определена функция, может быть разбит на конечное число интервалов, в каждом из которых функция непрерывна и монотонна.

2. Функция в области определения непрерывна или имеет конечное число разрывов первого рода.

Теорема Дирихле.

Пусть функция задана на некотором сегменте и удовлетворяет на нем условиям Дирихле. Тогда функция может быть разложена на этом сегменте в сходящийся к ней ряд Фурье по ортогональной системе функций.

В точке непрерывности функции , где- сумма ряда Фурье.

В точке разрыва функции .

Связь между гладкостью функции и порядком малости коэффициентов Фурье

Теорема. Пусть функция определена на отрезке, разлагается на нем в тригонометрический ряд Фурье и непрерывна на нем вместе со своими производными доp –1 порядка включительно. Пусть Еслиp –ая производная функции кусочно непрерывна на интервале, то коэффициенты Фурье- бесконечно малые функции по отношению к.

Доказательство.

=.

Здесь - коэффициенты Фурье для функции.

Продолжая аналогично интегрирование по частям, получим

. Из этих соотношений следует

Из этого соотношения или непосредственно можно получить аналогичное соотношение для .

Поэтому , гдеили-n –ый коэффициент Фурье.

По следствию из равенства Парсеваля для коэффициентов Фурье самой функции и ее производных.. Следовательно,_. Теорема доказана.

Пример. Разложить в ряд Фурье функцию и построить график суммы ряда.

Продолжим заданную функцию периодически на всю ось. Тогда функция будет иметь разрывы первого рода в точках . В этих точках функциябудет принимать значение, равное, по теореме Дирихле, полусумме левого и правого пределов функции. В остальных точках значения функцийибудут совпадать.

Вычислим коэффициенты Фурье.

,

.

. Проверьте, выполнив интегрирование по частям.

Из таких разложений часто можно получать суммы числовых рядов.

Например, подставим в разложение , получим

.

Подставим в разложение , получим

.