2003_МИРЗАДЖАНЗАДЕ А.Хи др.-Основы технологии добычи г / 1

Ò à á ë è ö à 1.37

Усредненные значения С5+ для расчета по уравнению (1.65)

t, °Ñ			Значение С5+				Сумма	Среднее
	1	2		3	4	5
0	18	64,5		134,5	191	290	698	139,6
10	20,5	50		117,5	200	281	669	133,8
20	20	52		91	176	275	615,6	123
30	8	50,5		103	174,5	268	602	120
40	11	45		95	166	242	558	11,8
Сумма	77,5	262		541	907	242	–	–
Среднее	15,5	52,5		108	181,5	271	–	–

П ри мер. В табл. 1.37 приведены усредненные значения С5+, которые получены с помощью корреляционной матрицы, выражающей связь выхода конденсата из газа с такими факторами, как давление ð, температура t, содержание конденсата в добываемом газе С5+ и характеристический фактор.

Эмпирическая зависимость g îò Ñ5+ описывается уравнением типа

				ó = à0 + à1õ1 + à2 õ2.
Подобрав коэффициенты, получим
		gC	+	= −4,798 + 11,285		(C5+ ) + 8, 7857		(C5+ )2 .	(1.65)
		5
Средние значения, вычисленные по этому уравнению, достаточно близки к
исходным средним:
gC	+	… … .. .....................................			1	2	3	4	5
5
Значение С5+:					15,5	52,5	108	181,5	271
среднее......................................
вычисленное.........................					15,3	52,9	108,1	180,9	271,2

Для устранения влияния фактора С5+ вычтем из приведенных данных полученные по эмпирической формуле средние значения (табл. 1.38), определим эмпирическую зависимость средних отклонений от второго по степени воздействия фактора. Эта зависимость хорошо описывается формулой

		gt2	= 14, 46 − 0, 764 + 0, 002t2.						(1.66)
			Ò à á ë è ö à 1.38
	Усредненные значения С5+ для расчета по уравнению (1.66)
t, °Ñ			Значение С5+					Сумма	Среднее
	1	2		3	4		5
0	2,5	12		26,5	9,5		19	69,5	13,9
10	5	–2,5		9,5	18,5		10	40,5	8,1
20	4,5	–0,5		–17	–5,5		4	–14,5	–29
30	–7,5	–2		–5	–7		–3	–24,5	–4,9
40	–4,5	–7,5		–15	–15		–29	–69	–13,8
Сумма	0	–0,5		–1	+0,5		1	–	–
Среднее	0	–0,1		–0,2	0,1		0,2	–	–

69

Для сравнения вычисленные по уравнению (1.66) и средние значения t приведены ниже:

gC	+	… … ........................................	0	10	20	30	40
5
Значение t, °Ñ:
среднее.....................................			13,9	8,1	–2,9	–4,9	–13,8
вычисленное ..........................			14,1	6,7	–0,3	–6,9	–13,2
Полученные эмпирические формулы объединим в одну:
g = 9,37 – 0,764t + 0,002t2 + 11,28(C5+) + 8,785 + (C5+)2.								(1.67)
В это уравнение не вошли факторы				l	è ð, так как ими пренебрегли в си-
				K

лу их слабого влияния.

Для оценки точности полученной формулы найдем коэффициент множественной корреляции: R = 0,99, что свидетельствует о хорошей сходимости экспериментальных и расчетных данных.

П ри мер. Ранее с помощью ассоциативного анализа и ранговой классификации решали задачу об установлении связи между коэффициентом увеличения добычи конденсата из пласта и факторами, характеризующими термодинамиче- ское состояние и состав пластового газа. В результате были отобраны четыре наиболее информативных признака: пластовое давление, начальный конденсатный фактор q, ñì3/ì3, температура выкипания 90 % конденсата t90 и параметр

F = (Ñ2 + Ñ3 + Ñ4)/Ñ5+.

В результате корреляционного и регрессионного анализа получено уравнение регрессии для определения коэффициента извлечения конденсата из

пласта:
K! = 109,566 − 0,115ð − 0,022q + 0,00021F − 0,00045t90.	(1.68)

Видно, что последними факторами при вычислении Kð можно пренебречь. Тогда формула будет иметь вид

K! = 109,566 − 0,115ð − 0,022q.

(1.69)

Возможность определения коэффициента извлечения конденсата по формуле (1.69) проверяли на 12 месторождениях США и четырех месторождениях СНГ. Средняя погрешность составила 5,5 %.

При составлении комплексных проектов разработки и обустройства газоконденсатных месторождений, а также для планирования добычи конденсата и его переработки необходимо располагать данными по выходу конденсата, т.е. количеству конденсата, поступающего из пласта с добываемым газом на поверхность, на весь период разработки месторождения.

В целях установления статистической связи между содержанием С5+ в добываемом газе и факторами, характеризующими состав пластового газа и термодинамические условия пласта, собраны экспериментальные данные по потерям конденсата в пласте для 32 месторождений из разных районов СНГ. По этим данным построены кривые изменения содержания конденсата в добываемом газе. Для сопоставления эти кривые перестраивали в безразмерных пара-

метрах ó = qäi/q0 è õ = ði/pí.ê, ãäå qäi – содержание конденсата в добываемом газе, см3/ì3; q0 – потенциальное содержание С5+ â ãàçå, ñì3/ì3; pi – пластовое

давление, МПа; ðí.ê – давление начала конденсации, МПа.

Ряд таких кривых для пластовых газов различных конденсатных месторо-

70

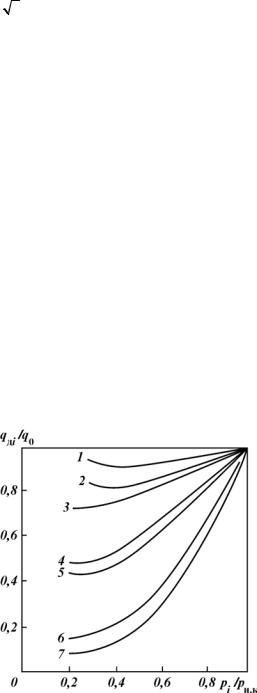
ждений представлен на рис. 1.22. Анализ этих кривых показал, что они могут быть достаточно точно описаны уравнением типа

ó =	à	åbx.	(1.70)
õ

Для установления аналитической связи между коэффициентами à è b уравнения и составом добываемой пластовой смеси были взяты на кривой зна- чения ó ïðè õ = 0,5. Затем с помощью метода ранговой классификации были выявлены наиболее информативные признаки, влияющие на найденные значе- ния ó ïðè õ = 0,5. С использованием корреляционного и регрессионного анализа было подобрано оптимальное сочетание параметров, характеризующее термодинамические параметры пласта. Средняя погрешность по этим месторождениям составила около 6,5 %.

Таким образом, используя формулу (1.70), можно рассчитать ó ïðè õ = = 0,5 для любой кривой, т.е. получить ординату точки на кривой изменения содержания С5+ в добываемом газе.

По значению ó ïðè õ = 0,5 рассчитывают коэффициенты à è b уравнения (1.68) при условии: если õ = 1, òî ó = 1, åñëè õ ≠ 1, òî ó ≠ 1. Затем строят графики изменения содержания С5+ в составе добываемого газа (см. рис. 1.22). Сопоставление проводили с данными, полученными как по константам равновесия, так и по кривым потерь конденсата в пласте. Наблюдалась хорошая сходимость предлагаемого метода с ранее существующим.

Многомерный корреляционный анализ. При многомерном корреляционном анализе уравнение регрессии можно представить в виде произведения функций отдельных факторов:

m

ói = y“! ∏Fi(xij). (1.71)

i=1

Вид функций Fi(xi) выбирается из следующей совокупности:

p, “.1.22.j!, "/å , ƒìå…å…, “%äå!›=…, *%…äå…“=2=" ä%K/"=åì%ì ã=ƒå " ƒ=", “, -

ì%“2, %2 %2…%øå…, ði/p….* äë ìå“2%- !%›äå…, L:

1 – )åëK=““*%å; 2 $ q2=!%ì,…“*%å; 3 $

r!å…ã%L“*%å (a35); 4 $ aå!åƒ=…“*%å; 5 $ r!å…ã%L“*%å (a3$10); 6 $ b3*2/ëü“*%å; 7 $ p3““*,L u32%!

71

	F	= a (x	+ a )a2	− a	; F = a la2 x − a ;			F	= 1/(a		+ a x)− a ;
	1	1	3	4	2	1	3	3		1	2	3
F		2	− a ;	F =	1/(a	+ a l−x )− a		;	F	= a (x + a )a2		la5 (x+a3 ); (1.72)
	= a la2 (x+a3 )
4	1		4	5	1	2	3		6	1	3
										r
	F7	= a1 + a2 ln(x + a3); F8 = a1 + a2 x; F9 = ∑al xl; r = 2, 3, 4.
										l=0

Введение в функцию Fi(xi) дополнительных параметров à3 è à4, сдвигающих значение функций по осям координат, делает совокупность функций более приспособленной к аппроксимации.

Определение уравнения регрессии вида (1.71) заключается в следующем. Значения зависимой переменной yi заменяют нормированными:

				1	n
y1i = yj	y“! ;	y“!	=		∑ yi.		(1.73)
				n j=1
Далее определяют эмпирическую линию регрессии						y1j	= F1(x1j) и рассчи-
						%

тывают значения остаточной функции ó2j = y1j/F1(x1j), равной произведению функций F2(x2j)F3(x3j) è Fm(xmj). Затем находят уравнение регрессии и рассчитывают значение следующего остатка:

ó3 j = y2 j / F2 (x2 j )= F3(x3 j )F4 (x4 j )...Fm (x2m ).

(1.74)

Цикл расчетов проводят до тех пор, пока не будут определены все функ-

öèè Fi(xij).

Из совокупности функций (1.72) наилучшей считается та, у которой сумма квадратов разностей между опытными и вычисленными по данной формуле значениями минимальная (метод наименьших квадратов). Эту функцию используют при составлении уравнения регрессии (1.71). Средняя квадратическая погрешность аппроксимации в зависимости Fi(xij)

	1	n
Si2 =		∑[yij − F(xij )]2 ,	(1.75)
	x j=1

ãäå i = 1, 2, … , m; j = 1, 2, ..., n.

Вычисление i-го приближения для значений óij проводят по формуле

	óij		i				(1.76)
			= yñð ∏Fk (xkj ).
	%
			k=1
Заменой переменных
	Uj = ln(yj + a4)(1/ y + a4);
V	= ln(x	j	+ a )(x	j	+ a )2	exp(−x	);
j			3		3	j
			Wj = (xj + a3)
уравнения для F1–F6 из совокупности (1.72) приводят к виду
			Uj = a1 + a2Vj.				(1.77)
Уравнение для F7 принимает вид

72

Uj

= a1 + a2Vj + a5Wj.

(1.78)

Коэффициенты à1 è à2 линейного уравнения (1.77) вычисляют по форму-

ëàì

1

n

2

1 n

2

à2

=

U“!V“!

−

∑UjVj

V“! −

∑Vj

;

(1.79)

n j=1

n j=1

a1 = U“! − à2V“!,

ãäå

1

n

1

n

U“! =

∑Uj;

V“! =

∑Vj.

n j=1

n j=1

Для нахождения коэффициентов à1, à2 è à5 уравнения (1.78) представим

åãî â âèäå

1

n

Dj =

∑[a1

+ a2Vj

+ a5(xj

+ a3)−Uj]2.

(1.80)

n

j=1

Дифференцируя уравнение (1.80) последовательно по à1, à2 è à5, ïîëó-

÷àåì

2 ∑[a1 + a2Vj + a5(xj + a3)−Uj];

∂Di

=

(1.81)

n

∂a1

j=1

∂Di =

2 ∑[a1 + a2Vj + a5(xj + a3)−Uj]Vj;

n

∂a2

j=1

∂Di =

2∑[a1 + a2Vj + a5(xj + a3)−Uj ](xj + a3).

n

∂a3

j=1

Систему уравнений (1.81) приводят к системе линейных алгебраических уравнений, которую решают по методу Гаусса с выбором главного элемента:

	n		n		n
à1n + a2 ∑Vj		+ a5 ∑(xj		+ a3)=∑Uj;
	j=1		j=1		j=1
n	n		n		n
à1 ∑Vj + a2 ∑Vj2			+ a5 ∑(xj		+ a3)=∑VUj j;	(1.82)
j=1	j=1		j=1		j=1
n	n		n		n
à1 ∑(xj + a3)+ a2	∑Vj (xj + a3)+ a5 ∑				(xj + a3)2 =∑Uj (xj + a3).
j=1	j=1		j=1		j=1

Коэффициенты à3 è à4 определяют последовательно методом локальных вариаций. Оптимальное значение коэффициента соответствует минимальной средней квадратической погрешности аппроксимации для данного вида аппроксимирующей функции, ее находят варьированием в интервале от –Syi äî Syi ñ

3		1	n	2
начальным шагом ry = Syi/Ky, ãäå Syi	=		∑	(yij − yi“! ). Значение Kó задают, оно
		n j=1

определяет точность результата и скорость счета.

73

Если на каком-либо шаге варьирования коэффициента à4 выполняется неравенство

r−1	2	r 2	r 2	(1.83)
[(Syi	) − (Syi )]/(Syi ) ≥ 0,05,

то текущее значение шага варьирования по независимой переменной Ró увели- чится на значение начального шага ry. В выражении (1.83) Syr−1 – средняя

квадратическая погрешность аппроксимации на предыдущем шаге. Выполнение неравенства (1.83) означает, что относительное уменьшение погрешности аппроксимации превышает 5 %. Увеличение шага варьирования сокращает время счета. Процесс варьирования заканчивают, если превышен интервал варьирования или предыдущее приближение лучше последующего.

Аналогичным образом определяют оптимальное решение параметра à3. Интервал варьирования изменяется от –Sxi äî Sxi, ãäå

	2		1	n	2
	Sxi	=		∑(xij − xi“! ).		(1.84)
			2
				j=1
	Начальное значение шага	варьирования			находят	из соотношения rxi =

= Sxi/Kx.

Аппроксимацию табличных значений Ei(xij) полиномом Fg степени r осуществляют с помощью ортогональных многочленов Чебышева. Сущность способа состоит в том, что аппроксимирующий полином ищут не в виде суммы степеней õ, а в виде комбинации ортогональных многочленов:

r
F(x)= b0T0 (x)+ b1T1(x)+ b2T2 (x)+...brTr (x)= ∑biTi(x).	(1.85)
i=1

Коэффициенты b0, b1, … , br определяют исходя из условия минимума суммы квадратов разности между опытными и вычисленными по рассматриваемой формуле значениями функции:

	1	n		r		2
Di =		∑	yij ∑biTi(xij) .				(1.86)
	n i=1			i=	0

Дифференцируя уравнение (1.86) по b и приравнивая к нулю полученные произведения, получаем систему уравнений для определения bi:

n	n		n
b0 ∑T0 (xj )Ti(xj )+ b1	∑T1(xj )Ti (xj )+ bi ∑Ti(xj )Ti (xj )+
j=1	j=1		j=1
n		n
+ ...+ br ∑Tr (xj )Ti (xj )= ∑ yiTi (xj ), i = 0, 1, … , r.				(1.87)
j=1		j=1
Принимая во внимание, что
n		n
∑Ti (xj )Tk (xj )= 0, i ≠ k;		∑Ti (xj )2	≠ 0, i = 0, 1, … , r,
j=1		j=1

получаем формулу для вычисления коэффициента разложения по ортогональным многочленам Чебышева:

74

		n			n
		bi = ∑ yiTi (xj )/∑[yiTi(xj )] 2 .								(1.88)
		j=1			j=1
Коэффициенты ортогональных многочленов Чебышева
	Ti+1(x)= (x + βi+1)Ti(x)+ γi+1Ti−1(x),									(1.89)
ãäå
							1	n
		T0(x)= 1;	T1(x)= x +					∑ xj;
							n j=1
		n				n
		∑ xi[Ti(xj)]2				∑ xijTi−1(xi)Ti(xi)
β	=	j=1	; γ	i+1	=	j=1			.	(1.90)
		n				n
i+1
		∑ [Ti(xj)]2				∑[Ti−1(xj)]2
		j=1				j=1

Группируя значения коэффициентов ортогональных многочленов по степеням, получаем ó = F(x) в виде многочлена r-й степени.

r

Функцию ó% = ∑ aixi вычисляют по схеме Горнера.

i=0

При использовании ортогональных многочленов Чебышева необходимо, чтобы аргументы õ1, õ2, … , õn функции ó = F(x) образовали монотонную последовательность.

Упорядочение массивов исходной информации по возрастанию аргументов осуществляют по методу Шелла. Идея метода состоит в следующем. Сначала следует обнаружить и упорядочить пары, состоящие из отдельных элементов, начиная с тех, в которых расстояние K между элементами составляет целую часть n/2 позиций. Затем просматривают пары с расстоянием K, равным целой части n/4, и так далее – до тех пор, пока n не станет равным нулю.

На заключительном этапе просматривают пары соседних элементов. Элементы каждой из групп упорядочивают методом сравнения и переменой мест тех элементов, у которых значение нижнего элемента меньше верхнего. В результате на первом шаге заключительного этапа на последнее место в массиве ставится элемент с самым большим значением признака. Затем свое место занимает следующий по значению признака элемент и т.д.

Для равных значений аргументов вычисляют среднее значение функции и объединяют значения равных аргументов. При этом осуществляют сдвиг элементов массива влево на число объединенных аргументов и корректируют число полученных вариантов массива.

П ри мер. Многомерный корреляционный анализ использовали для полу- чения уравнения регрессии, связывающего коэффициенты извлечения конденсата с факторами, которые характеризуют термодинамическое состояние пласта (давление, температура) и состав пластовой смеси. В качестве характеристики последнего при анализе использовали следующие параметры: конденсатный фактор G, ñì3/ì3; параметры F è À1, определяемые по формулам F = (Ñ2 + Ñ3 + + Ñ4)/Ñ5+, À1 = (Ñ1 + Ñ2 + Ñ3)/(Ñ4 + Ñ5+); содержание в пластовом газе этана С2, пропана Ñ3, бутанов С4, пентанов и вышекипящих Ñ5+ и их сочетаний –

À2 = Ñ2/Ñ3, À3 = Ñ2Ñ3, À4 = i = C4/n = C4, À5 = Ñ1Ñ5+, а также параметры, характеризующие общие свойства стабильного конденсата и его фракционный и

групповой составы: плотность ρê, молярную массу Ìê, параметр Ï = Ìêdê, выход фракции до 100 îÑ — g100 и температуру выкипания 90 % конденсата — t90,

75

а также параметр группового состава E = Càð/(Cìåò — Cíàô), ãäå Cìåò, Càð, Cíàô — массовое содержание ароматических, метановых и нафтеновых углеводородов

во фракциях соответственно.

Оценку влияния каждого из этих параметров на формирование коэффициента извлечения конденсата Kèçâ проводили с помощью ассоциативного анализа, позволяющего выявить наиболее информативные параметры. Информативность каждого параметра определяли по коэффициенту ассоциации ϕ и среднему квадратическому отклонению ϕñ (табл. 1.39): чем выше ϕ каждого параметра по сравнению с ϕñ, тем информативнее данный параметр.

При оценке информативности дополнительно учитывали предполагаемый вклад каждого фактора в искомые корреляции по абсолютным его значениям.

В качестве основных из 21 рассмотренного параметра были оставлены шесть: ð, Ìê, G, À4, F, C52+. Параметры Ï1 è Ï2 были исключены из списка ос-

новных ввиду редкости определения при анализе газоконденсатных смесей. Однако регрессионное уравнение, состоящее из шести переменных, являет-

ся громоздким. Для упрощения вида искомого регрессионного уравнения следует объединить ряд параметров, отражающих родственные свойства газоконденсатных смесей, в одну группу. Новые объединенные параметры имеют вид

D1 = 0,3 (2,6ð + G); D2 = 0,2 (F + C52

+ )+ 0,1M*.

(1.91)

Параметр D1 характеризует общие свойства газоконденсатных смесей, а D2 – состав смеси и свойства конденсата.

Многомерную корреляционную зависимость между Kèçâ (выходным параметром) и параметрами D1 è D2 (факторами), обусловливающими изменение Kèçâ, представляли в виде произведения отдельных факторов xij:

m

Kèçâj = Kèçâ.ñð iD=1(xij ), j = 1, n; i = 1, m,

ãäå Kèçâ.ñð – среднее арифметическое массива Kèçâ; n – число значений одного фактора; m — число факторов.

Ò à á ë è ö à 1.39

Результаты расчета показателя информативности

	Пределы из-	Показатель				Пределы из-	Показатель инфор-
Параметр		информативности			Параметр		мативности
	менения					менения
		ϕ	ϕñ				ϕ	ϕñ
G, ñì3	40–700	0,491	0,0813		C52+	0,1–110	0,364	0,0885
F	0,8–15	0,450	0,0269		ρ, ã/ñì3	0,65–0,8	0,392	0,0976
A1	5–15	0,239	0,0983		Ìê, êã/ìîëü	70–135	0,594	0,0746
C2	0,6–15	0,26	0,0961		Ï1	50–100	0,489	0,084
C3	0,5–8	0,167	0,1020		Ï2	100–165	0,420	0,0887
C4	0,5–3,5	0,117	0,1020		g100, %	4–5	0,440	0,0273
C5	0,4–13	0,329	0,092		t90	1,54–3,69	0,298	0,0763
A2	0,5–30	0,126	0,1040		E	0,04–1,7	0,24	0,0072
A3	0,01–20	0,261	0,0966		t, °C	50–150	0,16	0,0026
A4	0,3–10,5	0,470	0,1200
A5	2,5–95	0,350	0,0176

П р и м е ч а н и е . Значения C2, C3, C4, C5+ даны в молярных долях.

76

Вид функций Fi (xij) выбирают по минимуму средней квадратической погрешности аппроксимации из совокупности заданных функций: логарифмиче- ской, гиперболической, степенной, показательной, полиномиальной и их комбинаций.

Оказалось, что искомую зависимость можно аппроксимировать четырьмя корреляционными уравнениями, коэффициенты множественной корреляции R и дисперсии σ которых незначительно различаются (табл. 1.40). Для выбора наилучшего из них были рассчитаны Kèçâ газоконденсатных смесей, предварительно отобранных с помощью таблицы случайных чисел из исходного массива, состоящего из 107 смесей.

Таких смесей, не участвовавших в получении корреляционных выражений, оказалось 17, т.е. 15,8 % от общего числа. Для них также рассчитывали Kèçâ по корреляционному выражению.

В результате сравнения рассчитанных и экспериментальных значений Kèçâ для 17 смесей вычисляли коэффициент множественной корреляции R, остаточ- ную дисперсию σ2%“2, критерий Фишера F, дисперсию погрешностей σ2C :

n

2

∑

2

(Ki − Kip)

n

R =

1 −

σ%“2

; σ2%“2 =

i=1

; σ2x = ∑(Ki − K

)2;

2

n − m −1

σy

i=1

n

)2

2

∑(∆Ki − K

E =

σ%“2

;

σ2y =

i=1

;

(1.92)

σ2

n −1

y

n

∆Ki = Ki −

Kip; K = ∑ Ki n,

i=1

ãäå Ki, Kip – соответственно экспериментальные и рассчитанные значения коэффициентов извлечения; n – число значений Kèçâ; m – число коэффициентов корреляционного извлечения.

×åì âûøå R и меньше σîñò è σï, тем с большей точностью получают Kèçâ. Чем меньше значение Å, тем меньше погрешность расчета Kèçâ по 17 смесям и распределение погрешности вычисления Kèçâ (ñì. òàáë. 1.40).

Оказалось, что наиболее точным из рассмотренных пяти является третье уравнение, которое имеет вид

ln K	= 0,3704(à	åà2 p − à )(à
					+ à G			)[à + à ln(Ï				+	à )];
,ƒ"	1		3	4	5			6	7	2			8
		Ò à á ë è ö à 1.40
	Сравнение погрешностей результатов расчетов
									Количество точек
	Число ко-								(в % от общего					Средняя
		Статистический показатель							числа), вычислен-
Уравнение	эффициен-													арифметиче-
	тов уравне-								ных с погрешно-					ская погреш-
	íèÿ									ñòüþ, %				ность
		R	σîñò		E			σï	5	5–10			10
Kèçâ = f(Ï1, Ï2)	8	0,87	0,246		2,26			0,202	65	18			17	5,4
Kèçâ = f(Ï1, Ï2, À4)	15	0,65	0,574		8,03			0,184	70	17			13	4,2
Kèçâ = f(ð, G, Ï2)	8	0,91	0,174		1,65			0,170	82	6			12	3,7
Kèçâ = f(ð, G, Ï2)	14	0,79	0,573		3,90			0,177	70	17			13	4,1
По литературным	3	0,90	0,186		1,41			0,198	47	35			18	5,5
данным

77

p = p 269,6; G = G 202,6; Ï2 = Ï2 15,2 .

(1.93)

Коэффициенты уравнения: à1 = 0,82; à2 = 0,785; à3 = 0,7; à4 = 0,96; à5 = = 0,065; à6 = 0,95; à7 = 0,16; à8 = 0,44.

Метод группового учета аргументов. При построении многомерной статистической связи, исходя из регрессионного и корреляционного анализа, для оценки коэффициентов в уравнении регрессии используют статистическую выборку, а выбор вида функции и информативных признаков осуществляет сам исследователь.

Метод группового учета аргументов (МГУА) отличается от рассмотренных тем, что, используя идею эвристической самоорганизации малой выборки экспериментальных данных, позволяет выбрать вид аппроксимирующей функции и входящих в нее аргументов.

Âоснове МГУА лежит схема, по которой осуществляется шаговая селекция математических моделей процессов, приводящая, как правило, к выбору оптимальной, наилучшим способом описывающей рассматриваемый процесс. Алгоритм имеет вероятностный характер, т.е. вероятность получения лучшего решения растет с увеличением числа селекций.

Пусть задаются входные õ1, õ2, … , õn и выходная переменные и требуется по m наблюдениям найти зависимость y = f(x1, õ2, ..., õn). Для построения математической модели оптимальной сложности с помощью МГУА исходная

экспериментальная выборка делится на две последовательности (в каждой m2 наблюдений) – обучающуюся и проверочную. Обучающуюся последовательность используют в обычном регрессионном анализе для оптимизации оценок коэффициентов уравнения с помощью критерия минимума средней квадратической погрешности. Проверочная последовательность служит для выбора числа членов и конструкции уравнения регрессии минимизацией критерия селекции.

Âкачестве последнего выступает критерий регулярности σïð (средняя квадратическая погрешность построенной модели на экспериментальных точках

проверочной последовательности) или критерий несмещенности nñì (относительное смещение коэффициентов модели при определении их отдельно по обучающейся и проверочной последовательности). Выбор критерия исследователь осуществляет с учетом требований, предъявляемых к исходной модели. При этом следует иметь в виду, что критерий регулярности отбирает более точную модель, а критерий несмещенности – более устойчивую относительно исходных экспериментальных данных.

Для задач однократного прогноза целесообразно несколько снизить точ- ность определения коэффициентов уравнения регрессии, но за счет этого придать ему большую регулярность (прогнозирующую силу). Исходя из этого используют критерий регулярности

N

σ2C! = 1 ∑C! (yi − yi )2 , (1.94)

N i=1

ãäå Nïð – число точек проверочной последовательности; yi, yi – соответственно

прогнозное и действительное значения выхода в i-й точке.

Рассмотрим модифицированный упрощенный алгоритм по МГУА. Прежде всего отметим, что в целях получения компактного математического описания

78