2003_МИРЗАДЖАНЗАДЕ А.Хи др.-Основы технологии добычи г / 1

расширяют размерность вектора исходных данных добавлением к вектору x1

некоторых элементарных функций, таких, как 1/x, x è 1/ x. Таким обра-

зом, новый вектор исходных переменных z имеет размерность l = = 4n. На первом этапе составляют l линейных уравнений регрессии типа

y1(1i ) = a1(1i )z1i, i = 1, 2, … , l.

Коэффициент a1(1i ) для каждого из этих уравнений определяют отдельно для обучающейся и проверочной последовательности, после чего по формуле (1.94) для каждого уравнения находят σ2C!, по которой из l = 4n моделей отбирают r (r – заранее условленная величина, так называемая свобода выбора решений) наиболее перспективных (т.е. модели с минимальными σ2C! ). Äëÿ êàæ-

дого из перспективных решений первого этапа ϕ1(1f) (f = 1, 2, … , r) составляют l уравнений типа

y1(i2) = a1(i2)z1f z1i, i = 1, 2, … , l.

Определяют коэффициенты a1(i2) è σ2C! и снова отбирают r решений y1(f2).

Процесс направленного усложнения модели повторяют k ðàç (k – заранее условленная величина, так называемое число корреляций перспективного решения без увеличения числа слагаемых). Окончательно из совокупности моделей

y1(1f), y1(f2), … , y1(fk) отбирают модель, наилучшую в смысле минимума σ2C!, êîòî-

рая и является результатом первого ряда селекции.

На втором и следующих рядах селекции число слагаемых в частных описаниях увеличивают на одно по сравнению с предыдущим рядом. На каждом ряду селекции идет усложнение промежуточных описаний в результате добавления самих регулярных переменных. Так как частные описания являются функцией лишь одной переменной, а полное описание объекта получается сложением частных описаний, то ясно, что МГУА позволяет определять числовые значения сколь угодно сложного математического описания по малому числу экспериментальных данных.

Окончательно после n рядов селекции (число n рядов выбирают исходя из требуемой точности модели и качества исходной информации) модель имеет вид

S

y = A0 + ∑ AVi i, (1.95)

i=1

ãäå À0, Ài – коэффициенты модели; Vi – обобщенная переменная, структура которой определяется вектором z и процессом многорядной селекции.

Рассмотрим применение МГУА для получения моделей прогнозирования ðí.ê.

П ри мер. МГУА использовали для построения математической модели, описывающей связь ðí.ê пластовых газов с составом газоконденсатной смеси и температурой. Пределы изменения входных признаков, взятых для обучающейся выборки, приведены ниже:

79

Признак.......................................

изменения

ïðè-

Ñ1

Ñ2

Ñ3

Ñ4

Ñ5+

Пределы

знака.............................................

68,5–95,2

1–11

0,7–5,7

0,3–2,5

1,4–10,7

Признак.......................................

изменения

ïðè-

Ìê

ρê, ã/ñì3

tc ,

°C

p, ÌÏà

t , °C

Пределы

–35÷+35

знака.............................................

89–140

0,667–0,787

3,5–4

59–104

В результате расчетов было получено уравнение

À

À

1

t

2

ð

= À +

2

+

3

+ À

+

í.ê

1

Ìê ðñ

(Ñ5+)Ìêρê

4

Ñ3

Ìê ðñ

+

À

+ À6

Ñ (t +

50)

t

2

+

À

,

(1.96)

5

2

c

7

(Ñ5+)Ìê2ρê4

Ñ32

Ìê ðñ

(Ñ5+)Ìê2ρ7ê

ãäå Ìê, ρê – молярная масса, кг/моль, и плотность, г/см3, стабильного конденсата соответственно: ðñ, tñ – давление, МПа, и температура, °С, сепарации; t – температура опыта, °С.

Коэффициенты		уравнения:	À1	=	0,4238 103; À2 = –0,6131 106; À3 =
= –0,4332 104; À4	=	0,1605 106;	À5	=	–0,1426 106;	À6 = 0,9281 103; À7 =
= –0,5588 105.
Многорядная	селекция обеспечила				попадание в	уравнение наиболее ин-

формативных признаков, чем объясняется отсутствие в модели С1 è Ñ4.

Это уравнение дает хороший прогноз для залежей Тюменской области и Азербайджана.

Дискриминация моделей. Для описания того или иного процесса можно предложить несколько моделей, различающихся как по признакам, положенным в основу модели, так и по виду используемой функции или способу получения модели. При этом мера идентичности и средняя погрешность могут быть примерно одинаковыми.

Для того чтобы из всех предложенных моделей выбрать ту, которая наилучшим образом описывает процесс, прибегают к методу дискриминации моделей (метод Бокса – Хилла). При этом выбор часто обусловлен определенной областью применения модели, так как в зависимости от пределов изменения параметров модель может с достаточным приближением описывать одну область применения и плохо – другую. Поэтому при выборе той или иной модели следует исходить из интересующей области ее применения.

Естественно, что выбор модели осуществляют на основании экспериментальных данных. Пусть при изучении какого-либо процесса выполнено n экспериментов. Для описания полученных результатов предложено несколько моделей, характеризующихся одинаковой мерой идентичности. В этих случаях целесообразно проведение (n+1)-го эксперимента, на основе которого можно было бы установить, какая модель лучше.

Порядок проведения дискриминантного анализа следующий.

1. Оценивают параметры всех r предложенных моделей с помощью линей-

ной или нелинейной регрессии, а также дисперсий

σ2

è

σ2

:

y

r

1

n

1

n

σ2ó

=

∑(yi −

i)pi;

σr2 =

∑(yi − yi)pi,

(1.97)

y

n − 2

i=1

n − 1 i=1

ãäå yi – вычисленные по r-й модели значения; ði – число повторных изме-

рений.

2. Вычисляют для (n+1)-го эксперимента априорные вероятности либо за-

80

даются ими, исходя из эвристических соображений. Априорные вероятности (n+1)-го опыта являются апостериорными вероятностями для n-го опыта.

По теореме Бейеса апостериорная вероятность

pr(n) =	prn−1pr(y(n))	,	(1.98)
	n
	∑ prn−1pr(y(n))

r =i

ãäå pr(n −1) – априорная вероятность, относящаяся к r-й модели (если начальные

вероятности pr(0) известны, то их принимают равными 1/r); pr – плотность рас-

пределения вероятности наблюдаемого значения y(n) измеряемой величины в n-м опыте.

Äëÿ r-й модели

	(y(n)) =	1		−	1 (y(n) − y(n))2						(1.99)
p			exp					r		,
r		2 2			2 σ2			+ σ2
		2π(σy + σr )					y	r

ãäå y(n) è yr(n)– соответственно измеренное и вычисленное значения показателя

â n-м опыте.

Выбирают условия проведения (n+1)-го эксперимента, который позволит различить модели. Для этого находят максимум дискриминантной функции:

Kν =

1

ν ν

(n)

(n)

σ2r − σ2s

+

∑ ∑

pr

ps

(

2

2

2

2

2 r =1 s =r +1

σy

− σr

)(σy

+ σs )

1

1

+ (yr(n+1) − ys(n+1))

+

,

(1.100)

(σ2y

+ σ2r )

(σ2y + σ2s )

ãäå yr(n+1) – предсказанное (вычисленное) значение показателя на r-й модели в (n+1)-м опыте; индексы r è s относятся к номерам моделей.

Величину yr(n+1) определяют таким образом: задают значение аргумента

õ(n+1) и по предложенным моделям рассчитывают значение yr(n+1). Åñëè Kν íå

достигнет максимального значения, то проводят (n+1)-й эксперимент, уточняют параметры моделей и максимум функции Kν отыскивают в условиях (n+2)-го опыта.

Экспериментирование может быть прекращено, когда вероятности ðr станут столь различными, что можно будет отдать предпочтение одной из них.

П ри мер. Рассмотрим применение дискриминантного анализа при выборе модели для описания термодинамических свойств í-гептана. Были предложены следующие модели.

Модель 1:

p = K/V 3 + C/V 6,

(1.101)

ãäå ð – давление, Па; K = K0 + t/(a1 + b1t) – коэффициент, (см3/ã)3; C – êîýô-

фициент, (см3/ã)6; 1/Ñ = a2 + b2t; K0 = –4788,912; à1 = 0,045188; b1 = 0,3133 10–4; à2 = 0,34727255 10–4; b2= –0,354465 10–7.

81

p, “. 1.23. j!, "/å , ƒìå…å…,

pr " ƒ=", “, ì%“2, %2 n C!, !=ƒ- …/. 2åìCå!=23!=.:

1, 1′ $ 50$100 °q; 2, 2′ $ 150$ 200 °q; 3,3′ $ 250$300 °q

Модель 2:
	z =	pV	=1+	C	+	G	,	(1.102)
		RT
			V2		V6
ãäå ð – â Ïà; V –	â ñì3/ã; R =		8,31 ÌÏà ì3/(ã°C); T =					(t + 273,15), °C;
6	6
Ñ = ∑àntn, (ñì3/ã)2;	G = ∑bntn , (ñì3/ã)6; n – число атомов углерода в молеку-
0	0

ëå; à0 = –30,35; b0 = 118,65; a1 = 0,1952642; b1 = –0,306137; a2 = 0,5259329 10–3; b2 = –0,256141 10–3; a3 = –0,5079667 10–6; b3 = 0,1660393 10–4; a4 = 0,1014244 107; b4 = 0,120954 10–6; a5 = –0,316533 10–10; b5 = –0,3643413 109; a6 = 0,3148444 10–13; b6 = –0,38944 10–12.

Методика проведения дискриминантного анализа заключается в следующем. Сначала по первым n расчетным и опытным значениям удельных объемов вычисляют их средние значения yi ñð и определяют дисперсии каждой модели. Затем находят апостериорную вероятность правильности каждой модели. На- чальные вероятности Pi(0) можно приравнять к 1/m.

Описанную процедуру продолжают до тех пор, пока на основе значений вероятностей P не будет отдано предпочтение одной из моделей. На рис. 1.23, где представлены вероятности разных моделей при применении дискриминантного анализа, видно, что при 50, 100, 150 и 200 °С модели почти не отличаются одна от другой, а при 250 и 300 °С вероятность первого уравнения выше вероятности второго (P1(10) > P2(10)).

Учитывая, что уравнение (1.102) имеет более общий характер, так как охватывает большее число углеводородов – от С7 äî Ñ40, и что при температурах до 200 °С оба уравнения дают идентичные результаты, можно отметить, что при этих температурах в равной мере можно использовать оба уравнения.

При температурах более 200 °С точность уравнения (1.102) выше, и для описания термодинамических свойств í-гептана следует пользоваться им.

1.9. МЕТОД БЕЗЭТАЛОННЫХ ИЗМЕРЕНИЙ

При решении тех или иных технологических задач в промысловой практике часто приходится сталкиваться с отсутствием или недостатком необходимой исходной информации.

82

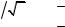
В этом подразделе приведена последовательность расчетов, позволяющая определять значения интересующего исследователя параметра не путем непосредственного его измерения, а на основе оценок значений других известных показателей, технологически с ним связанных. При этом требуется только один или два исходных измерения определяемого параметра. Данный подход основан на применении свойств порядковых статистик – одного из разделов непараметрической статистики. Простота и наглядность методики расчетов позволяют использовать ее непосредственно на промыслах.

Теория порядковых статистик изучает свойства объектов, занимающих определенные места (ранги) в упорядоченной выборке. Между значением элемента выборки и местом, которое он занимает после упорядочения, в ряде слу- чаев существует связь, позволяющая, ранжировав выборку, сделать оценки и выводы лишь по рангам элементов.

Поскольку можно упорядочить и те объекты, параметр которых неизвестен, теория порядковых статистик позволяет решать задачи идентификации объекта с ненаблюдаемым входом.

Рассмотрим общую схему проведения расчетов.

1.Известно, что два параметра õ è ó связаны между собой зависимостью

ó= g(x). При этом значение входной величины с известным законом распределения F(x) нельзя измерить непосредственно. Наблюдаемую величину ó можно измерить, но зависимость g(x) неизвестна. Известно лишь, что она монотонна. Под õ è ó понимаются значения дебитов скважин, расходов рабочего агента и других технологических показателей.

2.Выборка yi ранжируется в порядке возрастания. Так как известно, что зависимость ó = g(x) монотонна, то соответствующие результаты измерений yi è xi имеют одинаковые ранги, поэтому, кроме известных значений xi, имеются величины их рангов.

Связь между значениями переменной и величинами рангов выражается уравнением

R = 1 + (N – 1)Φ(õR),

(1.103)

ãäå R – ðàíã; N – число измерений выходного параметра ó; Φ(xR) – закон распределения случайной величины; xR = (x – mx)/σx; mx – математическое ожидание; σx – дисперсия.

3. По известному рангу опорного значения величины R из уравнения (1.103) определяют величину Φ(õ).

3.1. Если исходная выборка подчинена равномерному закону распределения, то

	õ ,õ ≤ x;
1
Φ(x)=	õ > x.
0,

Для определения известного параметра x требуется одна опорная точка (замер) и одно уравнение типа

R = 1 + (N −1)	xR			.	(1.104)
	x

3.2. Если исходная выборка подчинена нормальному и другим названным законам распределения, то для определения неизвестных параметров m и σ требуются как минимум две опорные точки и два уравнения.

83

4.По определенным параметрам законов распределения на основании уравнения (1.103) восстанавливается вся неизвестная выборка õ. Это осуществ-

ляется следующим образом. По известному рангу из уравнения (1.103) определяют Φ(xR), затем по таблице из [52] находят xR.

5.Так как зависимость y = g(x) монотонная, то связь между y è x можно описать уравнением

y = ag(x) + b.

(1.105)

Неизвестные коэффициенты находят с помощью метода наименьших квадратов. При этом решают систему из двух уравнений с двумя неизвестными

N	N	N	N	N
∑	ói = aN + b∑ g(xi ); ∑		ói xi = a∑ gxi + b∑ g(xi )3.		(1.106)
i =1	i =1	i =1	i =1	i=1

П ри мер. Значительную долю в комплексе мероприятий по контролю за разработкой месторождения составляют текущие измерения дебитов добывающих скважин. Представляет интерес по анализу предыдущей работы скважины определить необходимую длительность или частоту измерений для оценки с заданной погрешностью среднего дебита скважины на последующем этапе ее работы.

Однако длительность непрерывного измерения может быть значительной. В этом случае можно по двум фактическим результатам измерений оценить средний дебит скважины на основе применения аппарата теории порядковых статистик. Будем рассматривать выборку результатов измерений дебита скважины, упорядоченную, например, по возрастанию значений. Это можно сделать, не зная всех фактических значений дебита, по какому-то косвенному измерению, например, устьевого давления на данной скважине. При монотонном возрастании дебита скважины давление на устье будет монотонно снижаться и, наоборот, при уменьшении дебита – расти. Поэтому, зная значения устьевого давления в определенные моменты времени, можно ранжировать выборку дебитов в эти же моменты времени. Допустим, что в ранжированной таким образом выборке нам известны только два результата измерений дебита, а у остальных значений известен только ранг (порядковый номер в ранжированной, например по возрастанию, выборке).

Тогда с помощью методов теории порядковых статистик можно по двум имеющимся на определенном интервале времени результатам измерений дебита скважины и их рангам определить среднее значение дебита на этом интервале. Зная ранги остальных результатов измерений, можно оценить их значения и дисперсии этих оценок.

Необходимое условие этой процедуры – знание закона распределения измеряемой величины. В частности, для газовых и газоконденсатных скважин можно принять нормальный закон распределения дебита.

Для проверки гипотезы о нормальности закона распределения дебитов был проведен ретроспективный анализ результатов измерений дебитов газа сепарации, полученных в 1981 г. по скважинам УКПГ-2 Вуктыльского месторождения. Для примера приведем расчеты по скв. 116. Измерения дебита по этой скважине проводили через каждые 6 ч с 07.05.81 г. по 31.07.81 г.

Установлено, что данные о результатах измерений дебита не противоречат гипотезе о нормальности закона распределения значений дебита для этой скважины.

Проверку гипотезы о нормальности закона распределения в 1981 г. прово-

84

дили еще для восьми скважин Вуктыльского месторождения (скважины 119, 114, 3, 168, 121, 115, 111, 10). При этом только для скважин 10, 111, 115 значе- ния дебита не подчинялись нормальному закону распределения. Выборки результатов измерений по этим скважинам отличались значительной неоднородностью, что объясняется изменением технологического режима этих скважин по команде диспетчера. Для остальных скважин была принята гипотеза о нормальности закона распределения на основе критерия согласия Пирсона.

Процедуру оценки среднего за период исследований дебита по двум фактическим значениям проиллюстрируем на примере скв. 116 (табл. 1.41).

Представим данные табл. 1.41 в ранжированном виде: 798, 804, 805, 807, 808, 810, 811, 812, 813, 814, 815, 816, 818, 920, 822, 823, 824, 825, 826, 840.

Согласно контрольным измерениям 22.05.81 г. на скв. 116 буферное давление было равно 8,8 МПа, а 09.07.81 г. оно составило 8,6 МПа (на затрубье скважины установлен пакер). Дебиты газа сепарации при этом соответственно составляли 807 и 813 тыс. м3/ñóò (ñì. òàáë. 1.41).

Таким образом, снижению буферного давления на 0,2 МПа соответствовало увеличение дебита скважины на 6 тыс. м3/сут. Считая, что по образцовому манометру уверенно можно фиксировать разность давлений в 0,1 МПа, получа- ем, что изменение ранга значения дебита можно установить по манометру на буфере скважины в том случае, если дебит изменится не менее чем на 3 тыс. м3/сут. Тогда значения дебитов, представленные в табл. 1.41, можно отранжировать, используя показания манометра на буфере, следующим образом:

Ðàíã… ................................	1	2	3	4	5	6	7	8	9	10
Дебит..................................	798	804	807	810	813	816	819	822	825	840

В результате прямого измерения из этой последовательности, допустим, известны только два значения, соответствующие рангам 3 и 5: Q(3) = 807 è Q(5) = 813 òûñ. ì3/сут, а для остальных значений известен только ранг (по результатам измерений устьевого давления). Таким образом, используя результаты измерений устьевого давления и двух прямых измерений дебита скв. 116 22.05.81 г. и 09.07.81 г., после ранжирования по возрастанию значений проведем вычисления по формуле (1.103).

Ò à á ë è ö à 1.41

Результаты измерений дебитов скв. 116 Вуктыльского месторождения в 1981 г.

Äàòà	Дебит Q,		Äàòà	Дебит Q,		Äàòà	Дебит Q,
	òûñ. ì3/ñóò			òûñ. ì3/ñóò.			òûñ. ì3/ñóò.
Ìàé:			Èþíü:			Èþíü:
22	807		7	818		24	815
23	811		8	814		25	804
24	804		9	826		26	811
25	820		10	805		27	825
26	804		11	816		28	808
27	804		12	840		29	813
28	814		13	825		30	813
29	807		14	824		Èþëü:
30	813		15	820		1	811
31	798		16	810		2	805
Èþíü:			17	826		3	812
1	804		18	819		4	813
2	809		19	814		5	815
3	816		20	812		6	815
4	824		21	815		7	815
5	824		22	818		8	813
6	822		23	819		9	813

85

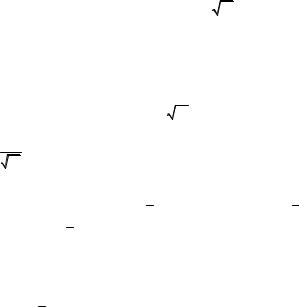
В рассматриваемом случае N = 10. Для нормального закона распределения значений дебита Q

1

z

FN

, σ) = FN (z, 0, 1) =

∫ e−u2 / 2 du,

(1.107)

(Q, Q

2π −∞

– среднее значение дебита; σ – среднее квадратическое

ãäå z = (Q – Q

) /σ; Q

отклонение.

Далее можно записать:

F (z,0,1)=

1

z e−u2 / 2

du,

(1.108)

N

2

π ∞∫

z

ãäå Φ(z) = 1 ∫e−u2 / 2 du – функция Лапласа.

2π 0

Ñучетом (1.102) получим 3 = 1 + (10 – 1)F [Q(3)]; 5 = 1 + (10 – 1)F [Q(5)], èëè F [Q(3)] = 0,2222; F [Q(5)] = 0,4444.

Ñучетом [17] имеем: (Q(3) – Q) /σ = –0,763; (Q(5) – Q) /σ = –0,140, откуда

σ= 9,63 òûñ. ì3/ñóò, Q = 814,4 òûñ. ì3/ñóò.

Определенные по всей выборке измерений по скв. 116 (N = 343) средний дебит и среднее квадратическое отклонение соответственно равны 816,5 и 11,1 тыс. м3/сут. Таким образом, относительная погрешность определения среднего дебита по абсолютной величине равна 0,26 %.

Найдя σ и Q , можно вычислить математическое ожидание Å[Q(i)] и дисперсию D[Q(i)] i-й порядковой статистики:

Å[Q(i)] = σli +Q

; D[Q(i)] = σ Vii,

(1.109)

ãäå li – математическое ожèдание; Vii – дисперсия i-й порядковой статистики, вычисленная при σ = 1 и Q = 0. Значения li è Vii затабулированы и зависят от N и закона распределения. Для li è Vii в случае нормального закона распределения и при N = 10, можно оценить значения дебита Q(i) по соответствующим рангам и определить дисперсии этих оценок (табл. 1.42).

П ри мер. При разработке морских газоконденсатно-нефтяных месторождений по ряду причин, связанных с технологией самой разработки, а также добычи, сбора и транспорта углеводородов, не всегда можно раздельно осущест-

Š = K ë , ö = 1.42

påƒ3ëü2=2/ !=“÷å2%" äåK, 2=C!, !=ƒ…/. !=…ã=.

p=…ã	li	n öå…*= äåK,2=,	Vii	d,“Cå!“, %öå…*,,
		2/“.ì3/“32		2/“.ì3/“32
1	$1,5388	799,6	0,3443	31,9
2	$1,0014	804,8	0,2145	19,9
3	$0,6561	808,1	0,1750	16,2
4	$0,3758	810,8	0,1579	14,7
5	$0,1227	813,2	0,1511	14,0
6	+0,1227	815,6	0,1511	14,0
7	+0,3758	818,0	0,1579	14,7
8	+0,6561	820,7	0,1750	16,2
9	$1,0014	824,0	0,2145	19,9
10	+1,5388	829,2	0,3443	31,9

86

вить измерения объемов добычи природного и нефтяного газа, нефти и конденсата. Среди упомянутых причин: способ разработки, при котором в продукции скважины представлены все четыре (помимо воды) вида продукции; естественные или искусственно создаваемые межпластовые перетоки; перемещение газонефтяного контакта; разгазирование нефтяной оторочки; использование неотсепарированной продукции газоконденсатных скважин на нужды бескомпрессорного газлифта; недостатки обвязки скважин, недостаточная надежность арматуры и задвижек; отсутствие достаточного количества обводных линий и замерных емкостей, вследствие чего на некоторых группах скважин, особенно расположенных на отдельных морских основаниях, можно осуществлять только совместные измерения. В связи с этим затрудняются контроль за разработкой отдельных залежей, оценка технологической эффективности методов интенсификации разработки, подсчет запасов углеводородов.

Задача заключается в восстановлении с достаточной для практики точностью динамики добычи природного газа, конденсата, нефти и нефтяного газа в отдельности при наличии регулярных измерений объемов добычи жидкости и газа по скважине или группе скважин и нескольких (не менее двух) измерений какого-либо физико-химического параметра смеси, позволяющего оценить ее состав.

Рассмотрим отрезок времени t, разделенный на интервалы ∆ti (i = 1, … , N), для которых известны значения добычи углеводородной жидкости и газа. Оче- видно,

qi = qi	+ qi	;	Qi = Qi	+ Qi	,	i = 1, … , N,
1	2		1	2

ãäå q – добыча углеводородной жидкости; qi – добыча конденсата; Q – добыча нефти; q2 – добыча газа; Q1 – добыча природного газа; Q2 – добыча нефтяного газа.

При этом содержание конденсата и газовый фактор

K = q1 Q1 ; Ã = Q2/q2.

(1.110)

Тогда

qi

=

K

Qi

− Ãqi

;

qi

= K

qi − KQi

;

(1.111)

1

1 − KÃ

2

1 − KÃ

Qi

=

Qi − Ãqi

;

Qi

= Ã

qi − KQi

.

1

1

− KÃ

2

1

− KÃ

Данные параметры неизвестны. Далее из соотношения

qj / q

j

= (ρ

i

− ρ

)/(ρ

…

− ρ

),

(1.112)

1

j

*

ãäå ρi, ρj, ρí, ρê – соответственно плотность смеси, газа, нефти и конденсата, получим

q1	= −	KÃ	+		K		Q	, èëè y = a + bx.	(1.113)
q		1 − KÃ
				1 − KÃ q

Здесь x = Q/q – средний газовый фактор, значения которого известны для N интервалов времени; y = q1/q – содержание в жидкой смеси конденсата, значе- ния которого известны для Ì интервалов времени ∆ti.

87

Априорно известно, что для большинства случаев õ – случайная величина, подчиняющаяся нормальному закону распределения. Поскольку ó линейно зависит от õ, эта переменная также подчиняется нормальному закону распределения, т.е. все расчеты проводят так же, как и для предыдущих задач: по двум опорным точкам определяют m и σ, восстанавливают õ и рассчитываются коэффициенты à è b, с помощью которых оцениваются K è Ã по формулам K =

= b/(1 – a), Ã = –a/b, и, наконец, определяют Q1i , Q2i , q1i , q2i .

На основании изложенного рассмотрим задачу восстановления динамики добычи нефти, конденсата, природного и нефтяного газов по приконтактным скважинам месторождения Бахар. Задача заключается в разделении продукции скв. 13 месторождения Бахар, добывающей смесь нефти, конденсата, природного и нефтяного газов (табл. 1.43). Известны также результаты двух измерений плотности жидкой фазы, по которым были рассчитаны значения q1/q, составившие в марте 0,5833 и в сентябре 0,6361 (значение i соответствует номеру месяца в году).

После упорядочения величин Q/q методом порядковой статистики восстанавливают недостающие значения q1/q (òàáë. 1.44).

Математическое ожидание и дисперсию определяют из системы двух уравнений:

						y5		− m = σ			45				0,5833			− m = −0,32σ;
						y7 − m = σ						èëè			0,6361			− m = −0,11σ;
											47
									m = 0,6226;								σ = 0,1228.
											Ò à á ë è ö à 1.43
		Данные по ежемесячной добыче газа и жидкости месторождения Бахар
Месяц					Q,	3		q, ì3			Q/q,						Месяц				Q,		3		q, ì3			Q/q,
				òûñ. ì						òûñ. ì3/ì3											òûñ. ì							òûñ. ì3/ì3
Январь				16 602				3777			4,396					Èþëü					11 986				4084			2,935
Февраль				13 370				3685			3,628					Август					13 238				4423			2,993
Ìàðò				13 440				4444			3,024					Сентябрь					14 478				4161			3,479
Апрель				13 170				4382			0,005					Октябрь					16 716				4123			4,054
Ìàé				14 110				4920			2,868					Ноябрь					13 985				3828			3,653
Èþíü				14 364				4353			3,300					Декабрь					13 928				3786			3,679
											Ò à á ë è ö à 1.44
					Данные для расчета содержания конденсата и газового фактора
k		i			Q/q				q1/q				K − 0,5				− 0,5			Uk = Ô–1		K − 0,5				− 0,5		yk
														N
																							N
1		5			2,868				–					–0,458							–1,73							0,4101
2		7			2,935				–					–0,375							–1,15							0,4814
3		8			2,993				–					–0,292							–0,81							0,5231
4		4			3,005				–					–0,208							–0,55							0,5551
5		3			3,024				0,5833					–0,125							–0,32							0,5833
6		6			3,300				–					–0,042							–0,11							0,6091
7		9			3,479				0,6361					–0,042						0,11								0,6361
8		2			3,628				–					0,125						0,32								0,6619
9		11			3,653				–					0,208						0,65								0,6901
10		12			3,679				–					0,222						0,81								0,7221
11		10			4,054				–					0,375						1,15								0,7638
12		1			1,396				–					0,458						1,73								0,8350

88