Предел функции.

Определение1 (по Гейне): Пусть задана функция f из некоторого множества , точка внутренняя точка , если , , то .

Определение: Окрестностью точки называется любое открытое множество, содержащее в себе некоторый открытый шар с центром в точке .

Определение2 (по Коши): , если f определена в некоторой окрестности точки ,

за исключением, быть может, самой точки (в ), и выполняется условие

Определения по Коши и по Гейне эквивалентны, доказательство этого проводится аналогично доказательству для функций одной переменной.

Теорема1 (критерий Коши существования предела функции):

Существование конечного предела функции эквивалентно выполнению условия Коши: выполняется условие Коши:

Доказательство аналогично случаю с одной переменной.

Свойства пределов функций многих переменных.

Теорема1 (ограниченность сходящейся функции):

Если функция имеет конечный предел , где – конечное или бесконечное, то ограничена в некоторой выколотой окрестности точки ( в ).

.

Теорема2 (о сохранении знака):

Если функция имеет конечный предел и , а – конечное или бесконечное, то существует окрестность такая, что . Более того, , и .

Теорема3 (предельный переход под знаком неравенства):

Если в некоторой выколотой окрестности , то .

Теорема4: (лемма о двух милиционерах):

Если в некоторой выколотой окрестности , и , то .

Теорема5: (арифметические свойства пределов):

Пусть , где A и B – конечные, – конечное или бесконечное, то

1.

2.

, где С – константа

3. Если

Пределы по направлениям.

Пусть задана функция , определенная в некоторой .

Рассмотрим произвольный вектор , тогда, так как функция определена в некоторой окрестности точки, она будет определена для всех точек вида , тогда можно рассмотреть уже функцию одной переменной: . И можно рассмотреть ее предел. Этот предел называется пределом функции по направлению .

Пример 1. Пусть у нас задана функция n переменных .

Мы можем рассмотреть в качестве единичный вектор, направленный вдоль одной из осей.

и предел ; Если рассмотреть минус единицу, то будет по противоположному направлению. Двумерный случай рассмотрен на рисунке.

Очевидно, что если существует , то . Это необходимое условие существования предела.

По определению предела , тогда мы нашли сферу радиусом , для всех точек которой выполняется такое неравенство, но тогда и для любого направления найдется такая точка , что для будет аналогичное неравенство выполняться уже для всех точек, лежащих на этом направлении. И предел по каждому направлению будет равен тому же самому числу A. Это условие не является достаточным.

Пример 1.

Рассмотрим . Она определена везде, кроме точки . Будем рассматривать . Имеем право рассматривать такой предел, поскольку функция определена везде в выколотой окрестности. В самой точке функция по определению предела может и не быть определена. Мы получаем, в силу того, что

Пример 2. . Пусть , тогда видим, что предел зависит от направления, то есть предел функции не существует.

П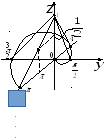ример 3. Покажем, что равенство пределов по направлению не является достаточным для существования предела. То есть нужно привести пример такой функции, что по всем направлениям пределы одни и те же, но предела у функции не существует.

Построим функцию двух переменных следующим образом: в плоскости зададим спираль (уравнение ). Пусть на спирали и за ней значение функции равно 0 и пусть . И соединим каждую точку спирали с точкой прямой, то есть зададим линейную на этом луче функцию.

Найдем, например, значение функции в точке с координатами : так как функция линейна и , , значит .

Получаем, что какое бы направление стремления к началу координат мы не взяли, значение функции будет стремиться к 1: . Однако сколь бы маленькую окрестность точки мы не взяли, в ней всегда найдутся нулевые значения, т.к. значение функции на спирали и за ней = 0.

Таким образом, предел равный единице существовать не может, а не равный единице он тоже не может существовать, так как пределы по направлениям равны 1. То есть, несмотря на то, что пределы по каждому направлению равны между собой, однако у функции предела нет.