Perekhodnye_protsessy_lektsii

=	*
			.
	'	( )
		$ ∆ (

Подставим (17.13) в (17.10):

( )∙+

∙

∙+

= −

∆

= −

!

(

$

)∙

!

Подставим (17.13) в (17.12):

( )∙+

∙

∙+

= −

∆

= −

!

!

(

$

)∙

!

!

= − !

$ !

= −
			$
			!

(17.14)

(17.15)

(17.16)

Для определения напряжения с одной из сторон продольной несимметрии (в данном случае обрыв одной фазы) предварительно по схемам отдельных последовательностей симметричной части цепи находятся соответствующие составляющие этих напряжений.

Прибавив к кА, кА, кА значения ∆ , ∆ , ∆ определяются симметричные составляющие напряжений с другой стороны продольной

несимметрии. Зная симметричные составляющие токов и напряжений можно определить фазные значения токов и напряжений. Для этого можно использовать выражения аналогичные (13.53) и (13.56). В этих выражениях ток

( , )	, сопротивления	и заменяется током и сопротивлениями
кА
и .
	Для нахождения модуля фазных токов при обрыве одной фазы можно

использовать коэффициент, определяемый аналогично .(/)(см. таблицу 14-2 учебник Ульянова).

Векторные диаграммы напряжений по концам разрыва в точках 0 и 01 (рис. 17.1) имеет вид:

Рис. 17.2

3

Векторная диаграмма токов в месте разрыва:

Рис. 17.3

17.3. Разрыв двух фаз

I&A L	L′
I&B
	&
&	UB
I
C	&
	UC

Рис 17.4

Граничные условия:

В = 0;	(17.17)
С = 0;	(17.18)
∆ А = 0;	(17.19)

Эти условия аналогичны граничным условиям однофазного короткого замыкания.

В соответствии с (17.17), (17.18) следует, что для фазы А можно записать соотношение:

= = =		.	(17.20)

4

В соответствии с (17.19) можно записать:

∆ + ∆ + ∆							= 0	(17.21)
							;
Сложим правые части уравнений (17.1) – (17.3):
− ∙	− ∙ − ∙ = 0;							(17.22)
С учетом (17.20) запишем (17.22):
− ( +					+ ) = 0
=			*
						,		(17.23)
		'			( )
				$ ∆ (
где ( ) = + .
∆
Из (17.20) выражение для фазного тока:
	= 3							(17.24)

Симметричные составляющие разности фазных напряжений обратной и нулевой последовательности из (17.2), (17.3) запишутся:

∆

∆

= − * ∙

' $ ∆( )(

= − * ∙!

' $ ∆( )(

=− ∙ ;

=− ∙ .

Из (17.21) получим выражение для ∆ :

∆ = −∆ − ∆ = ∙ + ∙ = (

∆ = ∙ ∆( ).

(17.25)

(17.26)

+)

(17.27)

5

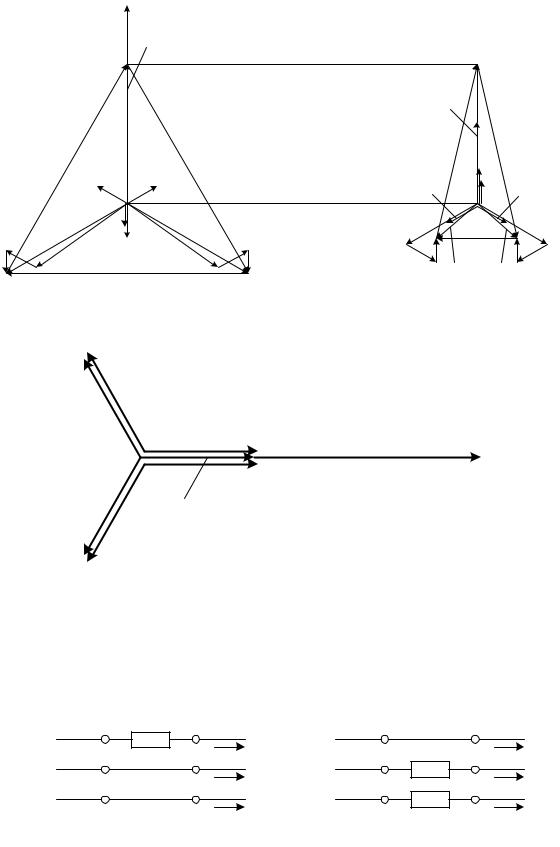
Векторные диаграммы напряжений по концам разрыва (в точках L и L’) имеет вид:

Рис. 17.5

Векторная диаграмма токов в месте разрыва:

Рис. 17.6

17.3. Несимметрия от включения сопротивлений

Считаем, что в одну или две фазы включаются одинаковые сопротивления 5(рис. 17.7).

Рис. 17.7

6

Такую несимметрию можно рассматривать как шунтирование сопротивлений 5 в фазах B и C или в фазе А (рис. 17.8).

Рис. 17.8

Если фазы В и С закорочены, то можно для фазы А записать:

∆ = 5 ∙

(17.28)

Два других граничных условия запишутся:

∆ В = 0

(17.29)

∆ С = 0

(17.30)

Для фазы А так же можно записать:

∆ + ∆ + ∆ = 5 ∙

(17.31)

∆ = ∆ = ∆ = ∙ ∆

(17.32)

Согласно второму закону Кирхгофа запишем:

∆ = − 6

∙

(17.33)

∆ = 0 − 6

∙

(17.34)

∆ = 0 − 6

∙

(17.35)

Выражение (17.28) распишем через симметричные составляющие:

7∆ + ∆ + ∆ 8 = 5( + + ).

(17.36)

7

Согласно (17.32):

3∆ = 5( + + ).

(17.37)

Выразим , из (17.34) и (17.35) с учетом (17.32):

= − ∆9 ;

= − ∆9 .

!

Подставим выражение для , в (17.37):

3∆ = 5( − ∆9 − ∆9 );

!

∆ = : (

− ∆9 − ∆9 );

!

:

:

;

+

( =

∆ +

∙ ∆ '

9!

9

∆ '1 +

:

9

$9

:

∙

9

∙ 9 !

( = ;

!

Преобразуем выражение в скобках:

:( 9 $9!

)

=

9

∙ 9! $:( 9 $9!

)

1 +

9

∙ 9

9

∙ 9

.

!

!

∆ =

5

∙

3 6

∙ 6

∙ ;

3

3 6

∙ 6

+ 5( 6

+ 6

)

∆ = : 6

6

∙ ;

(17.38)

= 5

( )

,

(17.39)

∆

∙

∆

где 5∆( ) – дополнительное сопротивление в схеме прямой последовательности.

Сопротивление 5∆( ) учитывает сопротивление 5, включённое в фазу.

8

Из (17.32) следует:

∆ = ∆ ; ∆ = ∆ ;

Из (17.33) получим:

5	( )
		∙ =		− 6 ∙
∆
		=		*
						.
			9		$:( )
					∆

Из (17.34) имеем с учетом (17.39 а):

5∆( ) ∙ = 6 ∙ ;

:( )

= − 9∆ ∙ .

(17.39 а)

(17.39 б)

(17.40)

(17.41)

17.4. Правило эквивалентности прямой последовательности

Ток прямой последовательности при продольной несимметрии определяется как ток симметричного трехфазного режима в схеме, где несимметричный участок заменен симметричной цепью, величина сопротивления которой для каждого вида продольной несимметрии определяется сопротивлениями как самого несимметричного участка, так и схем обратной и нулевой последовательностей относительно места несимметрии.

Ток прямой последовательности можно выразить в общем виде:

(/)			*
	=				;	(17.42)
				(=)
		9 $:∆
(/)	= 5		(/)	(/)		(17.43)
				∙ .
		∆

9

Применительно к (17.42), (17.43) принципиальная схема имеет вид

(рис. 17.9):

Рис 17.9

Правило эквивалентности прямой последовательности применимо только для основной гармоники.

Правило эквивалентности прямой последовательности позволяет применять для расчета переходного процесса практические методы расчета коротких замыканий.

10

ЛЕКЦИЯ №18

Однократная продольная несимметрия (окончание)

18.1. Комплексные схемы замещения

Рассмотрим комплексную схему при включении сопротивления в одну фазу (рис. 18.1).

Рис. 18.1

Полученные выражения для ∆ , ∆ , ∆ в месте рассматриваемой продольной несимметрии позволяют составить

комплексную схему замещения (рис. 18.2)

∆ = ∆ = ∆ = ∙ ∆ .

Рис. 18.2

Данные схемы удобны для расчета на моделях, расчетных столах, которые в настоящее время для расчетов уже не используются.

1

18.2. Распределение напряжений

При продольной несимметрии напряжение прямой последовательности по концам несимметричного участка отличается только по величине, напряжение обратной и нулевой последовательностей отличаются также по знаку.

Эпюры напряжений при разрыве одной фазы линии имеют вид (рис

18.3).

Рис 18.3

По мере удаления от места продольной несимметрии степень искажения векторной диаграммы напряжений снижается, т. к. вырастает относительное значение напряжения прямой последовательности.

Если сохраняется предшествующая ЭДС источника, то напряжение прямой последовательности до места разрыва оказывается выше предшествующих.

18.3. Применение принципа наложения

Неполнофазный режим можно представить как результат наложения на предшествующий режим собственно аварийного режима при условии, что в месте разрыва введен источник тока (− ) и все ЭДС из схемы удалены.

2