
- •Методические указания и контрольные задания
- •«Экономико–математические методы»
- •Рецензенты:
- •Оглавление
- •Введение
- •1. Методы решения задач линейного программирования. Теория двойственности в линейном программировании
- •Требуется:
- •Решение
- •Рассмотрим экономическую интерпретацию двойственной задачи. Двойственная задача соответствует следующей экономической проблеме.
- •2. Транспортная задача и методы ее решения
- •Решение
- •3. Решение матричных игр
- •Решение
- •4. Решение задачи линейного программирования в табличном процессоре Excel
- •5. Анализ решения задачи линейного программирования в табличном процессоре Excel
- •6. Решение транспортной задачи в табличном процессоре Excel
- •7. Вопросы для выполнения контрольной работы по экономико–математическим методам для студентов экономического факультета заочного отделения
- •8. Задачи для контрольной работы по экономико–математическим методам для студентов экономического факультета заочного отделения
- •Задача № 2
- •9. Литература
- •10. Правила выполнения и оформления контрольной работы
Введение
В методических указаниях рассматриваются основные типы задач по дисциплине «Экономико–математические методы», изучаемой студентами экономических специальностей заочной формы обучения.
Методические указания служат руководством для студентов – заочников при самостоятельном выполнении контрольных заданий по дисциплине «Экономико–математические методы».
С их помощью в условиях дефицита учебной литературы студент – заочник может самостоятельно разобраться в основных типах задач и без посторонней помощи справиться с выполнением контрольных заданий.
1. Методы решения задач линейного программирования. Теория двойственности в линейном программировании
На предприятии имеется возможность выпускать 2 вида продукции P1 и P2. При её изготовлении используются ресурсы R1, R2 и R3. Размеры допустимых затрат ресурсов ограничены соответственно величинами b1, b2 и b3. Расход ресурса i–го вида (i=1, 2, 3) на единицу продукции j–го вида составляет aij единиц. Цена единицы продукции i–го вида равна ci ден. ед. Найти план выпуска продукции по видам с учётом имеющихся ограниченных ресурсов, который обеспечивал бы предприятию максимальный доход.
Требуется:
-
составить математическую модель задачи линейного программирования;
-
найти оптимальное решение задачи линейного программирования графическим методом;
-
найти оптимальное решение задачи линейного программирования симплексным методом;
-
записать двойственную задачу и дать ее экономическую интерпретацию;
-
используя оптимальное решение исходной задачи, найти оптимальное решение двойственной задачи;
-
указать наиболее и наименее дефицитный ресурс;
-
установить, целесообразно ли выпускать новую продукцию P3, на единицу которой ресурсы R1, R2 и R3 расходуются в количествах d1, d2 и d3 единиц, а цена продукции составляет z денежных единиц: d1=1, d2=2, d3=3, z=15
Все необходимые числовые данные приведены в таблице 1.
Таблица 1 – Исходные данные
|
Ресурсы и цены продукции |
Затраты ресурсов на производство единицы продукции (aij) |
Запасы ресурсов (размеры допустимых затрат, bi) |
|
|
P1 |
P2 |
||
|
R1 |
3 |
4 |
30 |
|
R2 |
2 |
1 |
16 |
|
R3 |
8 |
9 |
72 |
|
Цены продукции |
30 |
25 |
|
Решение
Для того чтобы, можно было использовать математические методы для нахождения оптимального решения, необходимо составить математическую модель задачи оптимизации.
Математическая модель - математическое описание исследуемого процесса или явления. Процесс построения математической модели называют моделированием.
Построение математической модели задачи оптимизации можно разбить на следующие этапы:
-
Определение границ объекта оптимизации. Выполнение этого этапа носит неформальный характер и выходит за границы математики.
-
Выбор переменных, значения которых можно менять и выбирать с целью достижения наилучшего результата.
-
Определение ограничений на переменные.
-
Выбор числового критерия оптимизации. Числовой критерий оптимизации – функция, зависящая от выбранных переменных; минимальное или максимальное значение которой необходимо определить. Числовой критерий оптимизации иначе называют целевой функцией.
Построим математическую модель задачи линейного программирования.
Исходя из условий задачи, невозможно установить границы объекта оптимизации. Поэтому перейдем ко второму этапу – вводу переменных.
Обозначим через x1 – объем продукции P1, а через x2 – объем продукции P2.
Составим систему ограничений. Предположим что, все затраты ресурсов растут прямо пропорционально объёму выпуска продукции. Более точно, допустим, что затраты при выпуске xi единиц продукции Pi описываются вектором (a1ixi, a2ixi, a3ixi), причем одновременное использование нескольких технологических процессов приводит к суммарным затратам. Также учтем, что переменные, исходя из экономического смысла, должны принимать неотрицательные значения. В итоге получаем следующую систему ограничений:
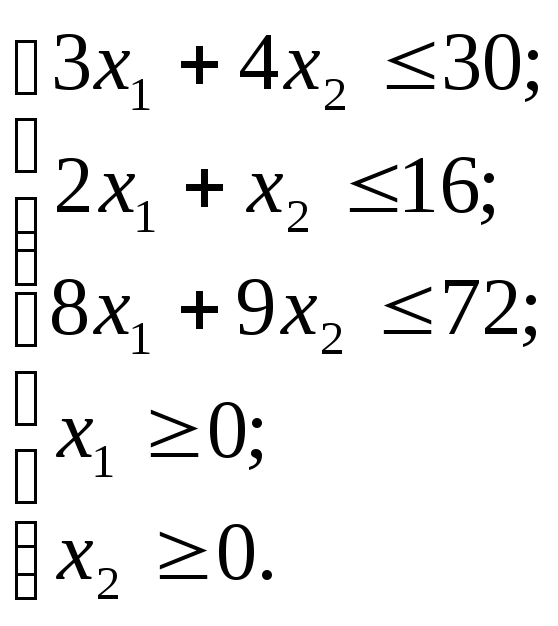
Запишем целевую функцию. Исходя из условия задачи, стоимость продукции должна быть максимальной. Стоимость продукции можно записать в виде следующей функции:
![]()
Окончательно математическая модель задачи имеет следующий вид:
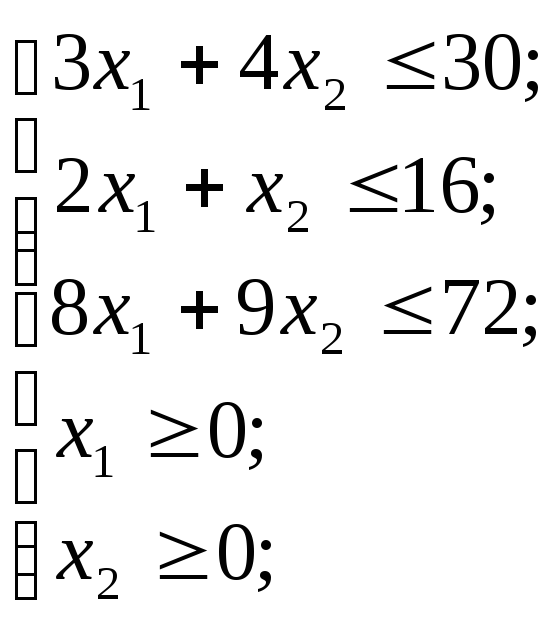
![]()
Математическая модель задачи представляет собой задачу линейного программирования, так как целевая функция и все функции в ограничениях являются линейными функциями.
Число переменных равно двум, поэтому значения переменных можно рассматривать как координаты точки на плоскости. Решим задачу линейного программирования графическим методом.
Решение задачи линейного программирования графическим методом можно разбить на два этапа.
1 этап - построение множества допустимых решений (допустимого множества).
Упорядоченный набор значений переменных (x1, x2,….xn) (иначе точка или вектор x с координатами (x1, x2,….xn)), удовлетворяющий ограничениям задачи линейного программирования называется допустимым решением (или планом) задачи линейного программирования. Множество всех допустимых решений задачи линейного программирования (далее, для краткости, ЗЛП) называется допустимым множеством этой задачи.
Построим множество
решений неравенства
![]() Для этого мысленно заменим знак
неравенства равенством и построим на
плоскости прямую, заданную уравнением
Для этого мысленно заменим знак
неравенства равенством и построим на
плоскости прямую, заданную уравнением
![]()
Найдем множество
решений неравенства
![]() Используем следующее утверждение. Если
две точки плоскости
Используем следующее утверждение. Если
две точки плоскости
![]() не лежат на этой прямой; то их взаимное
расположение относительно этой прямой
определяется знаками величин выражений
не лежат на этой прямой; то их взаимное
расположение относительно этой прямой
определяется знаками величин выражений
![]() и
и
![]() .
Если знаки величин выражений одинаковые,
то точки лежат по одну сторону от прямой;
если разные – по разные стороны от
прямой.
.
Если знаки величин выражений одинаковые,
то точки лежат по одну сторону от прямой;
если разные – по разные стороны от
прямой.
Возьмет точку O
и подставим ее координаты в выражение
![]() 3*0+4*0-30=30<0.
Знак выражения отрицательный, поэтому
множеством решений неравенства является
множество точек плоскости, лежащих ниже
прямой
3*0+4*0-30=30<0.
Знак выражения отрицательный, поэтому
множеством решений неравенства является
множество точек плоскости, лежащих ниже
прямой
![]() и
на самой прямой.
и
на самой прямой.
Неравенства
![]() означают, что множество решений
неравенства будет расположено в первой
координатной четверти.
означают, что множество решений
неравенства будет расположено в первой
координатной четверти.
В итоге множеством допустимых решений является прямоугольный треугольник AEO, который показан на рисунке 1.
Аналогично находим множество решений второго неравенства, учитывая условия неотрицательности, а затем находим пересечение множеств решений первого и второго неравенств.
Пересечением будет являться выпуклый четырехугольник AFDO.
Прежде чем строить
третью прямую
![]() ,
определим аналитически, как она
расположена относительно точки F
– точки пересечения первой и второй
прямых. Часто приходится приближенно
строить множество допустимых решений,
поэтому важно определить положение
прямых на чертеже.
,
определим аналитически, как она
расположена относительно точки F
– точки пересечения первой и второй
прямых. Часто приходится приближенно
строить множество допустимых решений,
поэтому важно определить положение
прямых на чертеже.
Найдем координаты точки F:
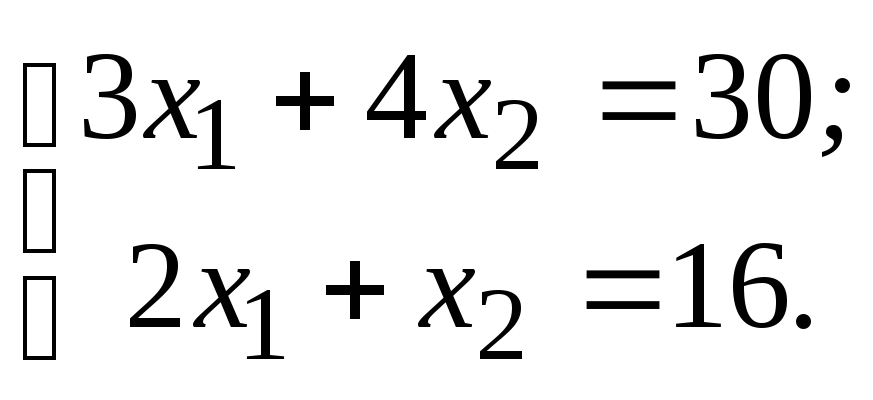
Решим систему линейных уравнений по правилу Крамера.
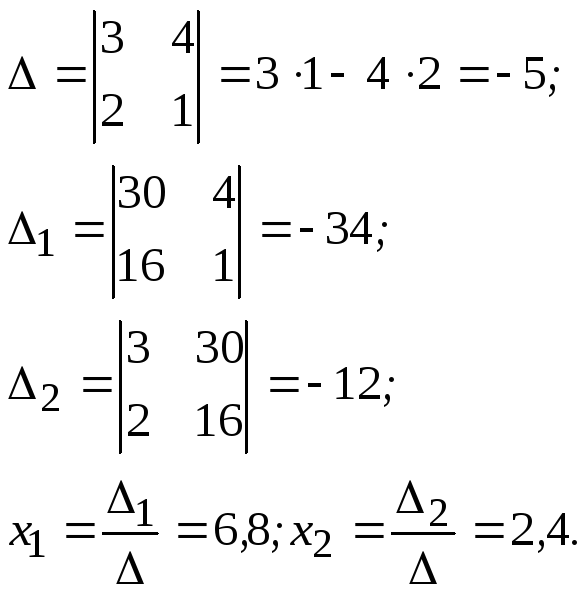
Точка F имеет координаты: F(6,8; 2,4).
Значение выражения
![]() в
точке O
отрицательно. Значение выражения
в
точке O
отрицательно. Значение выражения
![]() в точке F
положительно:
в точке F
положительно:
![]() .
Знаки выражений разные. Точка O
находится ниже третьей прямой, поэтому
точка F
находится выше третьей прямой.
.
Знаки выражений разные. Точка O
находится ниже третьей прямой, поэтому
точка F
находится выше третьей прямой.
Находим пересечение множеств решений первого, второго и третьего неравенств. Пересечением является выпуклый пятиугольник ABCDO.
Допустимым множеством для данной задачи линейного программирования является выпуклый пятиугольник ABCDO.



Рисунок 1 – Построение множества допустимых решений
2 этап - нахождение оптимальной точки в допустимом множестве.
Найдем точку, которая является оптимальным решением задачи линейного программирования (оптимальная точка).
Точка
![]() называется оптимальным решением задачи
линейного программирования, если,
во–первых, она является допустимым
решением этой задачи и если, во–вторых,
в этой точке целевая функция достигает
наибольшего значения (в случае задачи
максимизации) или наименьшего значения
(в случае задачи минимизации).
называется оптимальным решением задачи
линейного программирования, если,
во–первых, она является допустимым
решением этой задачи и если, во–вторых,
в этой точке целевая функция достигает
наибольшего значения (в случае задачи
максимизации) или наименьшего значения
(в случае задачи минимизации).
Для нахождения оптимальной точки используем следующую теорему.
Теорема. Пусть допустимое множество задачи линейного программирования является выпуклым многогранником. Среди точек, в которых целевая функция принимает максимальное (минимальное) значение, есть и крайняя точка. Если целевая функция принимает максимальное (минимальное) значение более чем в одной крайней точке, то она принимает это же значение в любой их выпуклой комбинации.
Из теоремы следуют два утверждения:
-
в допустимом множестве существуют точки, в которых целевая функция принимает наибольшее и наименьшее значения;
-
среди этих точек обязательно найдется крайняя точка.
Выпуклые многоугольники являются выпуклыми многогранниками. Вершины многоугольников являются крайними точками.
Поэтому план нахождения оптимальной точки для нашей задачи линейного программирования следующий:
-
найти координаты вершин пятиугольника;
-
вычислить значения целевой функции в этих вершинах;
-
среди найденных значений выбрать наибольшее число;
-
вершина, которая соответствует наибольшему числу, является оптимальной точкой. Значение целевой функции в этой точке является наибольшим значением целевой функции на множестве допустимых решений.
Найдем координаты вершин A, B, C, D. Имеем:
A(0;8), B(3,6;4,8), C(7,2;1,6),D(8;0)
Найдем значения целевой функции в этих вершинах:
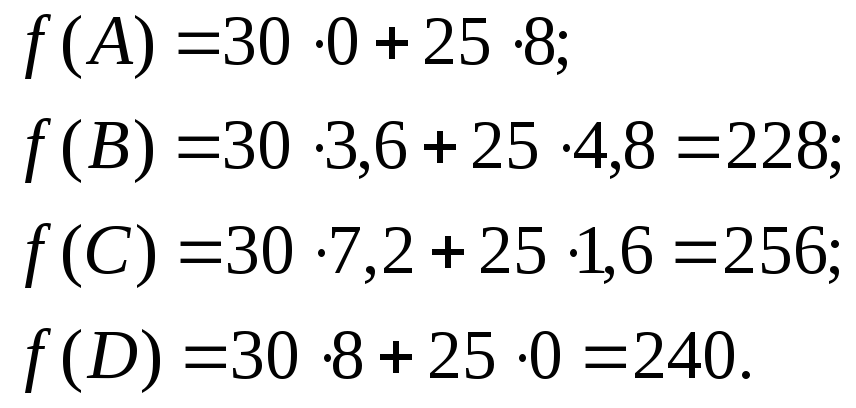
Оптимальной точкой будет вершина C.
Наибольшее значение целевой функции равно 256.
Решим данную задачу линейного программирования симплекс – методом.
Приведем задачу линейного программирования к каноническому виду.
Введем три дополнительные переменные x3, x4 , x5, которые принимают неотрицательные значения. В целевую функцию введем дополнительные переменные с нулевыми коэффициентами. Свободные члены в системе уравнений канонической задачи должны быть неотрицательными.
В результате получаем каноническую задачу линейного программирования с положительными свободными членами:
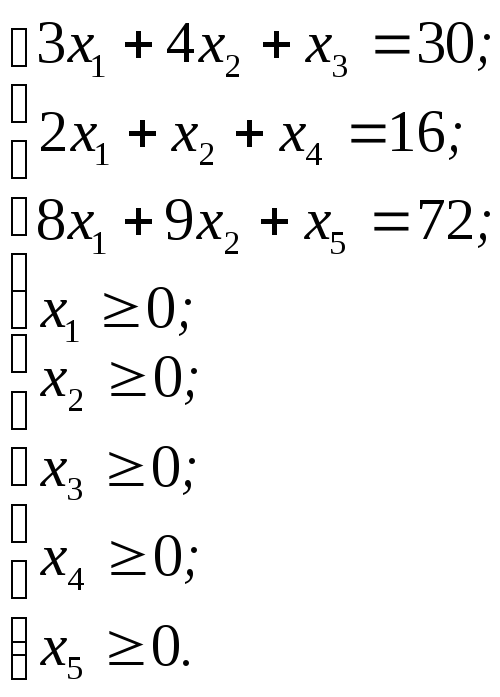
![]()
Находим начальное опорное решение. Для этого запишем матрицу коэффициентов системы линейных уравнений A.
Матрица A имеет следующий вид:

Матрица A содержит единичную матрицу третьего порядка, поэтому переменные x3, x4, x5 являются базисными; переменные x1, x2 являются свободными. Полагая свободные переменные равными нулю, получаем следующее начальное опорное решение: (0, 0, 30, 16, 72).
Заполним первую симплексную таблицу, которая показана в таблице 2.
Таблица 2 – Первая симплексная таблица
|
ci |
Базисные переменные |
Значения базисных переменных |
30 |
25 |
0 |
0 |
0 |
|
x1 |
x2 |
x3 |
x4 |
x5 |
|||
|
0 |
x3 |
30 |
3 |
4 |
1 |
0 |
0 |
|
0 |
x4 |
16 |
2 |
1 |
0 |
1 |
0 |
|
0 |
x5 |
72 |
8 |
9 |
0 |
0 |
1 |
|
|
Δ |
0 |
-30 |
-25 |
0 |
0 |
0 |
В первом столбце записаны коэффициенты у базисных переменных в целевой функции.
В третьем, четвертом, пятом, шестом, седьмом и восьмом столбцах записаны коэффициенты разложения столбца свободных членов и вектор - столбцов матрицы A, соответствующих переменным x1, x2, x3, x4, x5 по базису опорного решения. Так как базис является единичным, то эти коэффициенты совпадают с исходными значениями.
Оценки Δi вычисляем по формуле:
![]()
(Оценку Δi вычисляем как сумму произведений коэффициентов для базисных переменных в целевой функции на соответствующие элементы aji столбца Ai минус коэффициент ci в целевой функции.)
Значение целевой функции Δ0 при данном опорном решении заносится в последнюю строку третьего столбца,
![]()
где
![]() -
значения свободных членов
-
значения свободных членов
В нашем примере m=3 (число строк матрицы A равно 3), n=5 (число столбцов матрицы A равно 5).
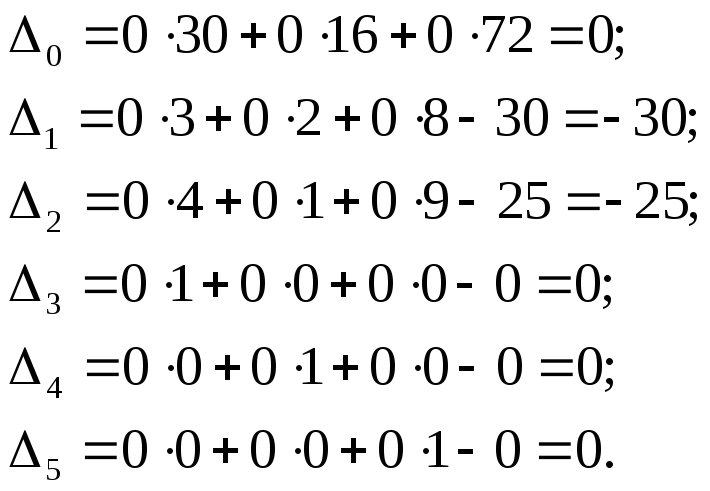
Отметим, что оценки для базисных переменных всегда равны нулю и в дальнейшем их можно не вычислять.
После заполнения первой симплексной таблицы переходим к этапам симплексного метода. Содержание этих этапов основывается на двух теоремах.
Теорема 1. Если оценки Δi (i=1,…,n) неотрицательные, то опорное решение является оптимальным.
Теорема 2. Если имеется отрицательная оценка Δk, то можно получить новое опорное решение, для которого значение целевой функции будет больше исходного; при этом могут быть два случая:
-
в столбце Ak все элементы неположительные, тогда целевая функция неограничена сверху на множестве допустимых решений - задача оптимального решения не имеет;
-
в столбце Aк существует хотя бы один положительный элемент, то возможен переход к новому, лучшему опорному решению, связанному с большим значением целевой функции.
Рассмотрим подробнее переход к новому опорному решению. Базис нового опорного решения отличается от старого лишь одним вектором. Геометрически это означает, что мы переходим от одной вершины к другой, двигаясь по ребру многогранника.
Переменная xk, которую необходимо ввести в число базисных переменных для улучшения решения, определяется по наименьшей отрицательной оценке Δk. Столбец, содержащий эту оценку, называется направляющим (в таблице помечен стрелкой).
В направляющем столбце определяем отношения (отношение) свободных членов к положительных элементам направляющего столбца. Из состава базисных переменных выводим переменную xr, на которой достигается наименьшее из этих отношений (в этом случае гарантируем переход к новому невырожденному опорному решению). Строка r называется направляющей (в таблице помечена стрелкой). Элемент ark, который стоит на пересечении направляющей строки и столбца, называется направляющим (в таблице обведен в рамку).
Далее переходим к новой симплексной таблице. Для этого направляющую строку делим на направляющий элемент (чтобы на месте направляющего элемента появилась единица) и пишем её на месте прежней. Из остальных строк таблицы вычитаем строку, полученную на месте направляющей строки, умноженную на такое число, чтобы элемент, стоящий в направляющем столбце, обратился в 0. Полученную строку пишем на месте прежней. Эти действия аналогичны операциям метода Жордана – Гаусса, который изучается в курсе линейной алгебры. На схеме показано как рассчитываются элементы строк таблицы.
|
Новое значение элемента, нахо-дящегося в i–й строке и в j– м столбце |
= |
Старое значение элемента |
|
Элемент матрицы, находящийся на пересе-чении направляющего столбца с i–й строкой |
|
Элемент обновленной направляющей строки в j–м столбце |
Иначе говоря, исключаем выбранную базисную переменную из всех строк симплексной таблицы, кроме направляющей строки. В результате из столбцов матрицы A, соответствующих базисным переменным, можно образовать единичную матрицу третьего порядка (переставляя при необходимости столбцы).
В нашем случае справедлив второй случай 2 теоремы. Переходим к новому опорному решению.
В число базисных переменных вводим переменную x1, так как она соответствует наименьшей отрицательной оценке. Столбец, соответствующий переменной x1, является направляющим.
Находим наименьшее отношение значений базисных переменных к положительным элементам в направляющем столбце:
![]()
Наименьшее отношение соответствует переменной x4, поэтому из числа базисных выводим переменную x4. Строка, соответствующая переменной x4, является направляющей строкой.
Элемент 2, который находится на пересечении направляющего столбца и направляющей строки, называется направляющим элементов. Он обведен в рамку. Переходим к новой симплексной таблице.
Все элементы направляющей строки делим на направляющий элемент: 2.
Исключаем переменную x1 из первой и третьей строки таблицы. Для этого, из элементов первой строки вычитаем элементы преобразованной направляющей строки, умноженные на 3. Полученные значения записываем на месте соответствующих элементов первой строки:
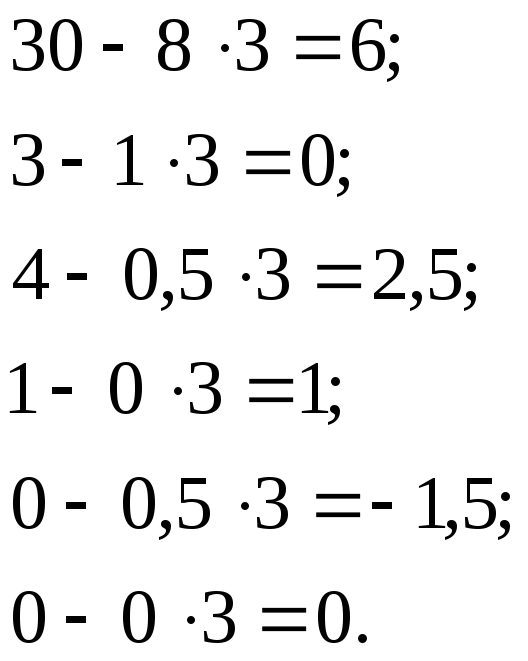
Находим элементы третьей строки симплексной таблицы. Для этого из элементов третьей строки вычитаем элементы преобразованной направляющей строки, умноженные на 8. Полученные значения записываем на месте соответствующих элементов третьей строки:

Находим оценки аналогично, как в первой таблице.
Результаты вычислений показаны в таблице 3.
Проверяем справедливость теорем 1 и 2.
Опорное решение не является оптимальным. Переходим к новому опорному решению, которое записано в 4 таблице.
Таблица 3 – Вторая симплексная таблица
|
ci |
Базисные переменные |
Значения базисных переменных |
30 |
25 |
0 |
0 |
0 |
|
x1 |
x2 |
x3 |
x4 |
x5 |
|||
|
0 |
x3 |
6 |
0 |
2,5 |
1 |
-1,5 |
0 |
|
30 |
x1 |
8 |
1 |
0,5 |
0 |
0,5 |
0 |
|
|
x5 |
8 |
0 |
5 |
0 |
-4 |
1 |
|
|
Δ |
0 |
0 |
-10 |
0 |
15 |
0 |
Таблица 4 – Третья симплексная таблица
|
ci |
Базисные переменные |
Значения базисных переменных |
30 |
25 |
0 |
0 |
0 |
|
x1 |
x2 |
x3 |
x4 |
x5 |
|||
|
0 |
x3 |
6 |
0 |
0 |
1 |
0,5 |
-0,5 |
|
30 |
x1 |
7,2 |
1 |
0 |
0 |
0,9 |
-0,1 |
|
25 |
x2 |
1,6 |
0 |
1 |
0 |
-0,8 |
0,2 |
|
|
Δ |
256 |
0 |
0 |
0 |
7 |
2 |
Все оценки Δi (i=1,…,5) в третьей симплексной таблице неотрицательные, поэтому опорное решение является оптимальным.
Подведем итоги решения задачи линейного программирования графическим методом и симплекс - методом. Запишем результаты решения в экономической интерпретации.
Оптимальный план выпуска продукции следующий: необходимо выпустить 7,2 единиц продукции P1 и 1,6 единиц продукции P2. Доход от производства этого плана будет наибольшим и составит 256 ден. ед.
Запишем двойственную задачу для данной задачи линейного программирования и дадим ее экономическую интерпретацию.
Предварительно рассмотрим понятие двойственной задачи и правила ее построения.
Пусть дана стандартная задача линейного программирования:
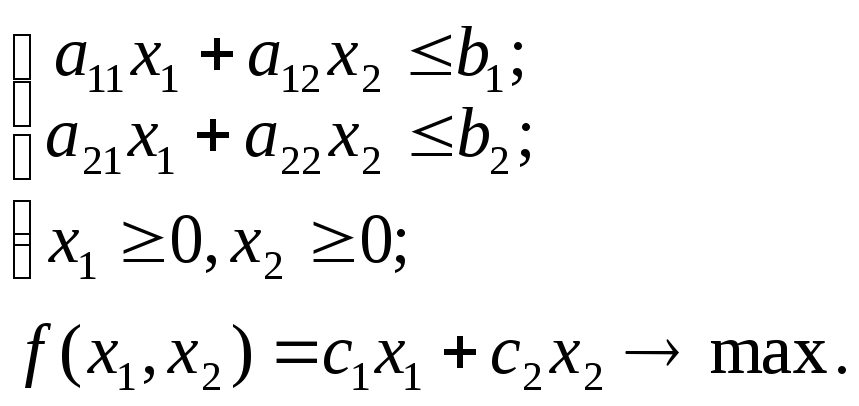 (1)
(1)
Задачей, двойственной к задаче 1, называется следующая задача линейного программирования:
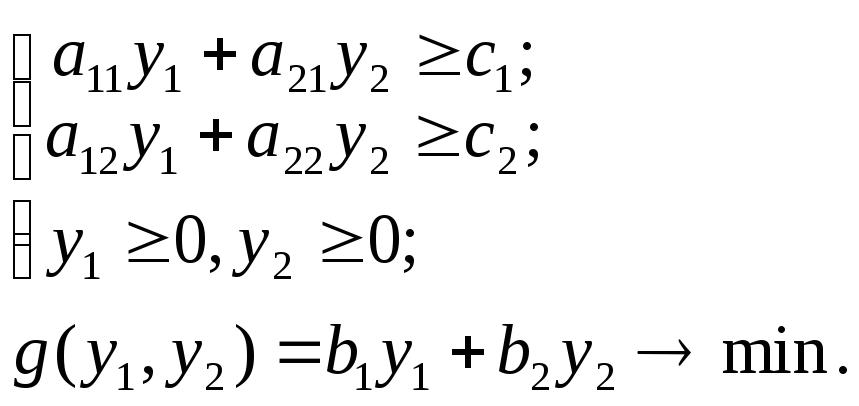
Аналогично можно записать двойственную задачу, если задача (1) имеет большее число ограничений и переменных.
Первая задача называется прямой задачей.
Правила построения двойственной задачи следующие:
-
число переменных двойственной задачи равно числу строк матрицы коэффициентов системы основных ограничений прямой задачи;
-
если прямая задача является задачей максимизацией, то двойственная будет задачей минимизации;
-
коэффициенты целевой функции прямой задачи становятся свободными членами ограничений двойственной задачи;
-
свободные члены ограничений прямой задачи становятся коэффициентами целевой функции двойственной задачи;
-
матрица коэффициентов системы основных ограничений двойственной задачи получается транспонированием матрицы коэффициентов системы основных ограничений прямой задачи;
-
знаки ограничений в системе основных ограничений двойственной задачи «».
Основные ограничения – все ограничения математической модели, кроме условий неотрицательности.
Запишем двойственную задачу для данной задачи линейного программирования.
Прямая задача:
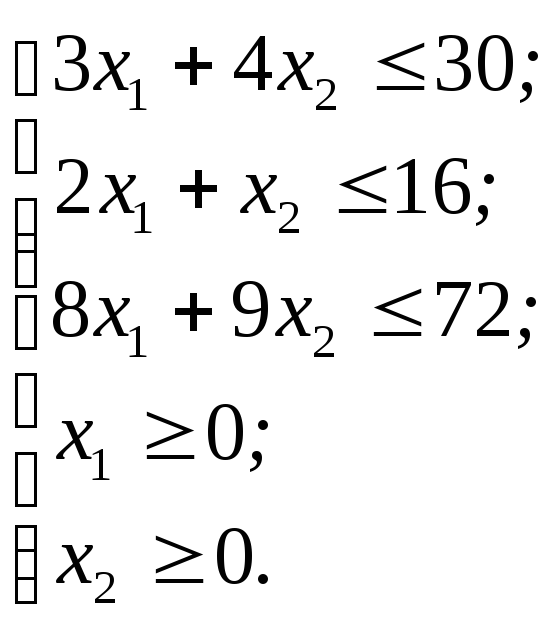
![]()
Составим двойственную задачу.
Введем три
переменные:
![]() ,
так как число ресурсов равно трем.
,
так как число ресурсов равно трем.
Запишем матрицу коэффициентов A:
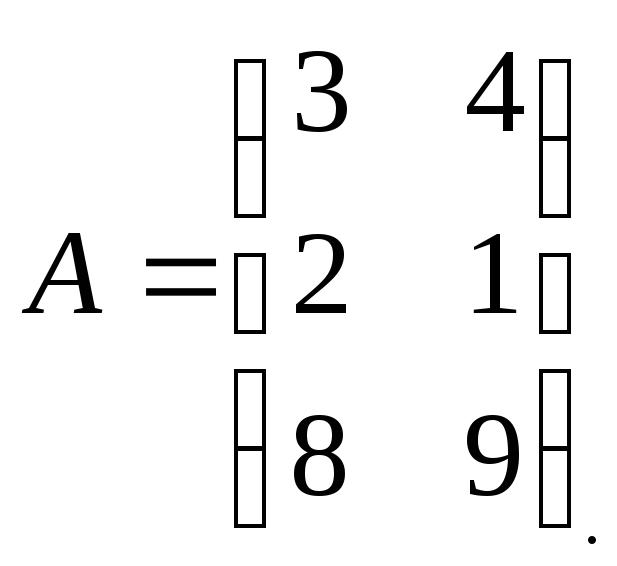
Транспонируем матрицу A:
![]()
Двойственная задача имеет следующий вид:
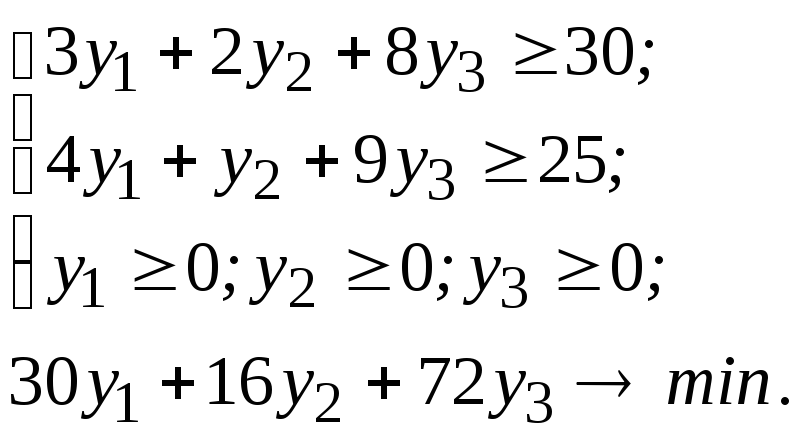


 0
0