Темы вопросов

11. Решение системы линейных уравнений. Теорема Кронекера-Капелли. 2

12. Решение невырожденных линейных систем. Формулы Крамера. 5

13. Метод Гаусса. Система линейных однородных уравнений. 6

14. Комплексные числа. Основные понятия. Геометрическое изображение. Формы записи комплексных чисел. 8

15. Действия над комплексными числами. 10

16. Уравнение линии на плоскости. Уравнение прямой. 12

17. Условие параллельности и перпендикулярности прямых. 14

18. Расстояние от точки до прямой. Окружность и эллипс. 16

19. Гипербола и парабола. Уравнение плоскости и прямой в пространстве. 18

20. Множества. Основные понятия. Свойства. 20

11. Решение системы линейных уравнений. Теорема Кронекера-Капелли.

Исторически первым, наиболее распространенным методом решения систем линейных уравнений является метод Гаусса, или метод последовательного исключения неизвестных. Сущность этого метода состоит в том, что посредством последовательных исключений неизвестных, данная система превращается в ступенчатую (в частности, треугольную) систему, равносильную данной. При практическом решении системы линейных уравнений методом Гаусса удобнее приводить к ступенчатому виду не саму систему уравнений, а расширенную матрицу этой системы, выполняя элементарные преобразования над ее строками. Последовательно получающиеся в ходе преобразования матрицы обычно соединяют знаком эквивалентности.

Система называется совместной, или разрешимой, если она имеет, по крайней мере, одно решение. Система называется несовместной, или неразрешимой, если она не имеет решений.

Теорема Кронекера-Капелли. Для того чтобы система была совместна, необходимо и достаточно, чтобы ранг основной матрицы системы равнялся рангу расширенной матрицы.

Определение. Если ранг матрицы системы равен рангу расширенной матрицы, т.е. , то ранг матрицы называют рангом системы.

Примечание. Если ранг системы равен числу неизвестных, то система определённая.

Теорема Крамера. Если матрица квадратной системы невырожденная, то система определенная.

В этом случае решение системы может быть найдено по формулам Крамера.

Формулы Крамера. Решение неоднородной системы уравнений с неизвестными, имеющей невырожденную основную матрицу системы, находится по формулам

, i = 1, 2, …, n

где – определитель системы; – определитель матрицы, получаемой из основной матрицы системы заменой её i-го столбца столбцом свободных членов.

Матричный метод. Если матрица А системы линейных уравнений невырожденная, т.е. det A ≠ 0, то матрица А имеет обратную, и решение системы совпадает с вектором . Иначе говоря, данная система имеет единственное решение. Отыскание решения системы по формуле называют матричным способом решения системы, или решением по методу обратной матрицы.

Примеры.

Решить систему уравнений

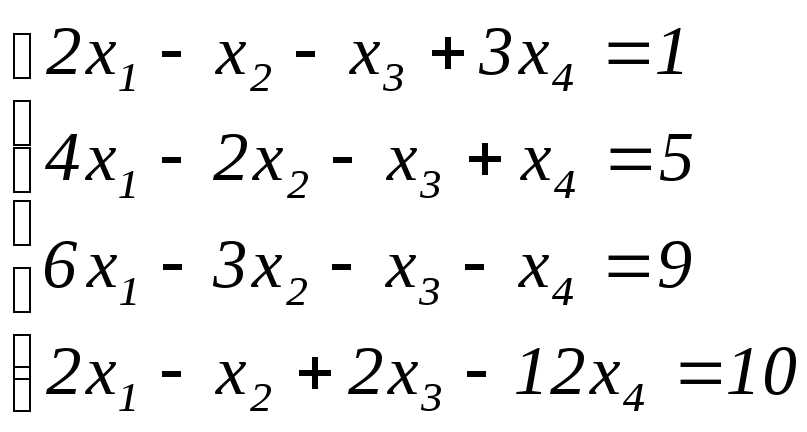
Решение. Будем решать методом Гаусса. Выпишем расширенную матрицу системы и преобразуем её, вычитая первую строку, умноженную на 2, 3 и 1 соответственно из 2-ой, 3-ей и 4-ой строк:

.

Далее вторую строку, умноженную на 2 и 3, вычтем соответственно из третей и четвёртой строк:

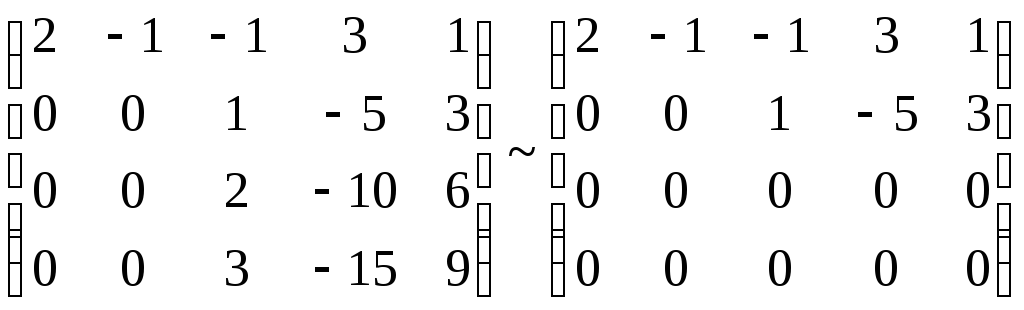
Последняя матрица эквивалентна следующей ступенчатой системе:

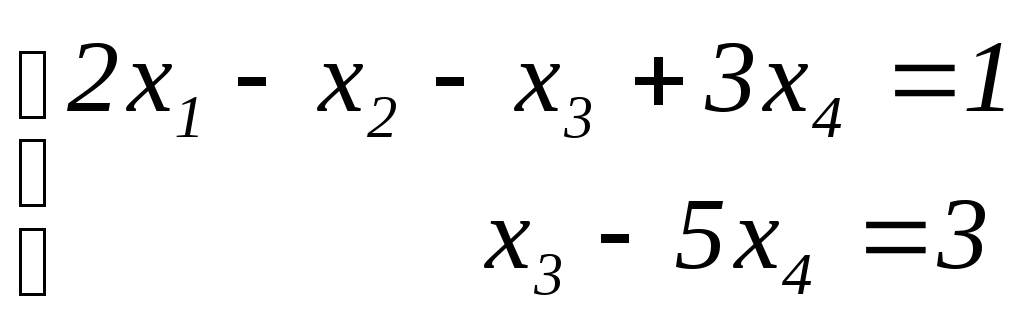
Полученная упрощённая система представляет собой систему из двух уравнений для четырёх неизвестных. Следовательно, два из неизвестных можно выбрать за главные, а два – за свободные, через которые будут выражены главные. В качестве главных неизвестных можно выбрать любую пару, если определитель, составленный из коэффициентов, стоящих перед ними, отличен от нуля (базисный минор). В данной задаче в качестве главных неизвестных можно выбрать .

Действительно, определитель, составленный из их коэффициентов, отличен от нуля:

.

Теперь из второго уравнения выразим через . Затем подставим его в первое уравнение и найдём через . В итоге получим

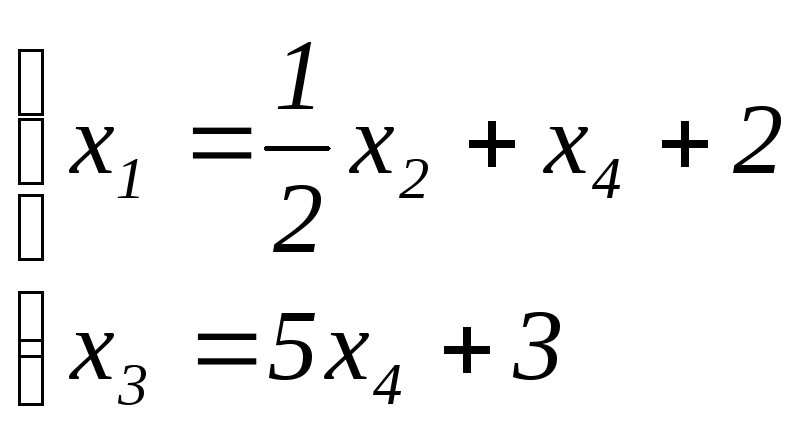
Переменные принимают произвольные значения. Положив , общее решение системы можно записать в виде:

.

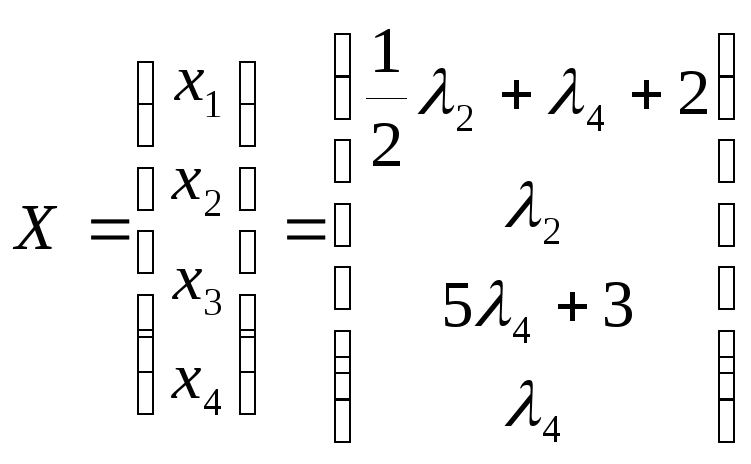Теорема. Если ранг однородной системы меньше числа неизвестных, то такая система имеет фундаментальную совокупность решений, состоящую из решений, где число неизвестных, ранг системы.

Определение. Совокупность решений однородной системы называется фундаментальной, если выполняются два условия:

1. эта совокупность линейно независимая;

2. любое решение однородной системы может быть линейно выражено через эту совокупность.