Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Тувинский государственный университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

практика алгебра 1.DOC

Скачиваний:

Добавлен:

15.11.2018

Размер:

2.26 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 1213 / 1613 14 15 16 > Следующая >>>

6.4. Доказательство от противного

Метод доказательства от противного основан на замене доказательства теоремы А  В доказательством равносильной ей:

а) А  В  А В  С С;

б) А  В  А В А;

в) А  В  А В  В.

В каждом из трех случаев рассуждение идет по следующей схеме: предполагается истинность условия и отрицания заключения теоремы, а затем доказывается, в первом случае, два противоречащих друг другу предложения С иС; во втором случае получаем противоречие с условием А; в третьем случае - противоречие с заключением теоремы.

П р и м е р 3. Во всяком треугольнике против равных углов лежат равные стороны.

ДОКАЗАТЕЛЬСТВО. Эта терема является обратной по отношению к теореме: во всяком треугольнике против равных сторон лежат равные углы.

Пусть в треугольнике АВС А = С, докажем, что

ВА = ВС.

Предположим противное, т.е. что ВА  ВС. Тогда одна из сторон должна быть больше другой, и, следовательно, согласно прямой теореме, один из углов А или С должен быть больше другого. Это противоречит условию, что А = С; значит, нельзя допустить, что стороны АВ и ВС не равны, поэтому АВ = ВС. ( Второй случай).

Теоретические вопросы:

Отношение следования и равносильности. Определение математических понятий. Теоремы. Взаимно обратные и противоположные теоремы. Необходимые и достаточные условия. Доказательство от противного.

6.1. Даны два предиката на R . Установите между ними отношение логического следования:

1. x > 1 и х > 2; 2. x  3 и x  5;

3. x < 4 и x < - 1; 4. x  3 и x  0;

5. ( x - 1) ( x + 2)=0 и ( x - 1 = 0)  ( x + 2 = 0);

6. x+ 6 + = 5x + и х- 5х + 6 = 0;

7. x- 1 = 0 и ;

8. х- 8х + 15 = 0 и ( х - 3 = 0)  ( х - 5 = 0)

9. | x | < 2 и x < 2 ; 10. | x | > 3 и x > 3;

11. | x - 1 |  2 и x  3; 12. | x + 2 |  1 и x  -3;

13. x > 2 и ; 14. x < 2 и ;

15. > 0 и 3 < x < 5; 16. 2 < x < 3 и >1.

6.2. Даны два предиката на некотором универсальном множестве U. Установите между ними отношение логического следования.

1. x  А и x  А \ В; 2. x  А и x  А  В;

3. x  А и x  А  В; 4. x  А  В и x А \ В.

6.3. Равносильны ли на множестве R следующие предикаты?

1. x = 0 и x ( x+1)=0; 2. х= х и =;

3. x + 1 =0 и (x + 1)=0; 4. 2x = 10 и (2х-10)(х+1)=0;

5. 7(x - 3) = 49 и х - 3 = 7; 6. x+5=x-1 и x(x-3)=x+8-3x;

7. и х - 3 >3(x - 1); 8. 2x>1 и 2х + х+3 >4+x;

9. х + 3 > 2 и х + + 3 > 2 + ;

10. 2x - 1 < 5 и 2x- x< 5x;

11. sin x + cos x = 1 и ( sin x + cos x)= 1;

12. = 1 и x- 1= 1;

13. = и x = 2x + 1;

14. = и 1- x = 2x;

15. log(x+2) = log(3 - x) и x + 2 = 3 - x;

16. lg (x + 1) = lg (2x + 3) и x + 1 = 2x + 3;

17. arcsin x = 1 и x = sin 1;

18. arcsin x = 3 и x = sin 3;

19. x x и x  1;

20. x> x и x> 1;

21. > x + 1 и x > (x + 1)

22. = x+ 1 и x > (x+ 1).

6.4. Запишите на языке предикатов определения:

1. - делимости целого числа n на целое число m;

2. - коллинеарности векторов а и в;

3. - ограниченной функции из R в R;

4. - периодической функции;

5. - наибольшего элемента на М относительно <.

6.5. Укажите род и видовое отличие в определениях четырехугольника, прямоугольника, ромба, квадрата, равнобедренного треугольника, равностороннего треугольника, трапеции.

6.6. Укажите ошибки в следующих определениях:

1. прямоугольник - это, когда все углы прямые;

2. отрезок - это прямая, ограниченная с двух сторон;

3. луч - это прямая, ограниченная с одной стороны;

4. простое число - это, когда оно имеет два делителя;

5. углом, вписанным в окружность, называется угол, образованный двумя хордами;

6. окружностью называется фигура, состоящая из всех точек, равноудаленных от данной.

6.7. Выделите условие и заключение в следующих теоремах и сформулируйте их в виде: “ Если..., то...” :

1. перпендикуляр к одной из двух параллелных прямых есть также перпендикуляр к другой;

2. вертикальные углы равны;

3. сумма углов треугольника равна 180;

4. диагонали ромба взаимно перпендикулярны;

5. сумма двух смежных углов равна 180;

6. против равных сторон треугольника лежат равные углы;

7. дуги, заключенные между равными хордами, равны;

8. диагонали параллелограмма делятся в точке пересечения пополам.

6.8. Для каждого из следующих утверждений сформулируйте обратное к нему, противоположное и противоположное к обратному утверждению. Укажите, истинно оно или ложно, дайте обоснование:

1. квадратное уравнение имеет корни только в том случае, когда его дискриминант неотрицателен;

2. если дискриминант квадратного трехчлена равен нулю, то его корни совпадают;

3. сумма корней квадратного трехчлена х+ px + q

равна - p, а произведение корней равно q;

4. квадратный трехчлен с неотрицательным дискриминантом можно разложить в произведение линейных множителей.

6.9. Вместо многоточия вставьте одно из выражений “ необходимо, но не достаточно”, “ достаточно, но не необходимо “, “ необходимо и достаточно” - так, чтобы получилось истинное высказывание:

1. а - четное число ... для того, чтобы 3а было четным числом;

2. а делилось на с ... для того,чтобы а,в делилось на с;

( а, в, с  Z);

3. а и в делятся на с ... для того, чтобы а + в дели-

лось на с ( а, в, с  Z );

4. делимость числа на 4 ... для того, чтобы оно дели- лось на 8;

5. свойства треугольника быть равносторонним ...

для того, чтобы он был остроугольным;

6. x  A ... x  A  B ;

7. x  A ... x  A  B ;

8. x  A ... x  A \ B ;

9. x  A  B ... x  A  B ;

10. x  A  B ... x  A \ B ;

11. x  A  B ... x  A \ B ;

12. ав = 0 ... для того , чтобы а = 0 и в = 0 ;

13. а < 2 и в < 5 ... для того, чтобы а + в < 7.

6.10. Для каждого из следующих утверждений о натуральных числах дайте три разные формулировки, используя слова: “ достаточно” , “ необходимо” , “ только тогда, когда” :

1. если а делится на 24, то а делится на 2 и на 3;

2. если а делится на 20 и на 30, то а делится на 60;

3. если произведение двух чисел делится на простое число р, то хотя бы один из сомножителей делится на число р;

4. если а делится на два различных простых числа, то а делится на их произведение;

5. если число имеет ровно два различных делителя, то оно простое.

6.11. Сформулируйте каждое из следующих утверждений о натуральных числах при помощи слов; “если..., то...” ;

1. для того чтобы число делилось на 12, достаточно,

чтобы оно делилось на 6 и на 4.

2. а делится на 12 только в том случае, когда а делится на 6;

3. для того, чтобы а делилось на 900, достаточно,

чтобы а делилось на 10 и на 6;

4. для того, чтобы а делилось на в, необходимо,

чтобы а делилось на любой простой делитель в;

5. число имеет не более двух различных делителей только тогда, когда оно простое или равно 1.

6. для того, чтобы а делилось на произведение bc, необходимо, чтобы а делилось на b и на с.

6.12. Руководствуясь определением импликации, сформулируйте:

1. достаточное, но не необходимо условие ложности импликации;

2. необходимое, но недостаточное условие ложности импликации;

3. необходимое и достаточное условие ложности им- пликации;

4. необходимое и достаточное условие истинности

импликации

6.13. Методом от противного докажите следующие теоремы:

1. в круге равные хорды одинаково удалены от центра и стягивают равные дуги;

2. в круге хорды, одинаково удаленные от центра, равны и стягивают равные дуги;

3. если одно из слагаемых делится на 7, а другое - нет, то сумма не делится на 7;

4. две прямые, параллельные третьей, параллельны;

5. если две параллельные прямые пересечены какой-нибудь прямой, то соответственные углы равны;

6. бесконечность множества простых натуральны чисел;

7.доказать, что число не является рациональным.

З А Н Я Т И Е № 7.

Прямое произведение множеств.

Теоретические вопросы.

Прямое произведение упорядоченного набора множеств. n -ая степень множества А. Прямое произведение двух множеств. Декартов квадрат множества А. Докажите, что А х В  В х А . В каком случае А х В = В х А ?. В каком случае А х В =?. Докажите: |А |= n , |В| = m , то |А х В| = n  m . Сформулируйте правило произведения.

7.1. Заданы множества А и В. Найдите:

а) А х В ; б) В х А ; в) ; г) ; д) А, если

1. А = {1,2}, В = {1,2,3} , 2. А = {3,4}, В = {0,1,2,5}

7.2. Найдите : 1) А х В , если А = 2Z, В = 3 Z.

2) А, если А = 3Z.

7.3. На координатной плоскости изобразите элементы множеств: а) А х В; б) В х А ; в) А г) В, если

1. А =[-1, 1], В = (-2, 1);

2. А = [-2, 2] , В = (0, );

3. А ={х R ; х > 4}; В = {5,3,4,1,9,8};

4. А = {х  R ; | х | 1}, В = {- 1, 0,5}.

7.4. Докажите, что для любых множеств А,В,С,Д.

1. А х (В  С) = (А х В)  (А х С);

2. (А  В) х С = (А х С)  (В х С);

3. (А  В) х (С Д) = (А х С) (В х Д);

4. А х (В U С) =(А х В) U (А х С );

5. А х (В \ С) = (А х В) \ (А х С);

6. (А U В) х С = ( А х С) U (В х С);

7. (А\ В) х С = (А х С) \ (В х C).

Решите задачи, используя правило произведения.

№ 1. Сколько имеется четырехзначных чисел, все цифры которых различна 

№2. Сколько имеется четырехзначных чисел, в записи которых встречаются одинаковые цифры 

№3. Сколько можно составить четных трехзначных чисел из цифр 1, 3, 4, 6, 7, в записи каждого числа соседние цифры различны 

№4. 1. Сколько трехзначных чисел можно записать, используя цифры 0, 1, 2, 3, 5, 7, 

2. Сколько среди них оканчивается цифрой 7 

3. Сколько таких , в которых 5 и 3 не стоят рядом 

4. Сколько из них не содержат цифру 0 

5. Сколько из них содержат только один раз цифру 3 

6. Сколько из них не начинается с цифры 5 

Решите задачу, если: А) цифры в записи числа не повторяются.

Б) цифры в записи числа повторяются.

№5 . Сколько имеется функций, удовлетворяющих условием: Д (f) = {1, 2, 3, 4, 5}, Е ( f) = {1, 2, 3, 4,} и (5) делится на (3)

№ 6. |А| = n , |В| = m. Сколько существует отображений множеств А во множество В ?

№ 7. А = {1, 2, ... n}. Сколько существует биективных отображений множестве А и А.?

№8. А = {1, 2... n }. Сколькими способами можно упорядочит множество А ?

№9. Сочетаниями называются подмножества конечного множества .Сочетаниями из n по к называются к подмножества n множества ( к  n). Символом С обозначается число сочетаний из n по к. 1.Объясните,почему?

а) С = С = 1 ; б) С = n; в) С =С .

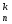Докажите: а) С = б) С + C=

З А Н Я Т И Е № 8.

Метод математической индукции.

Индукцией (от латинского слова inductio - наведение) называется метод исследования, познания, связанный с обобщением результатов наблюдений и экспериментов. В умозаключениях от частного к общему анализ данных опыта, зафиксированный в посылках, “наводит” на существование в них общего, что и фиксируется в заключении. Заключение может быть как истинным, так и ложным.

Речь идет об истинности предложения вида (n)P(n) (*) на некотором множестве А. Если множество А конечно и содержит немного элементов, истинность утверждения (*) устанавливается, как правило, перебором элементов.

П р и м е р 1. Доказать, что всякое четное натуральное число n, 4  n  100 представимо в виде суммы двух простых чисел.

Достаточно рассмотреть: 4 = 2 + 2; 6 = 3 + 3; 8 = 3 + 5;

10 = 3 + 7; ... ; 98 = 5 + 93; 100 = 3 + 97. Доказательство проведено разбором всех возможных случаев.

П р и м е р 2. Французский математик Пьер Ферма (1601-1665) рассматривал числа вида f(n) =+1. При n = 0, 1, 2, 3, 4 числа f(n) являются простыми. Действительно, f(0) =;

f(1) =; f(2) =; f(3) =

f(4) =. Ферма предположил, что все числа такого вида простые. Но через некоторое время Л.Эйлер показал, что уже следующее число f(5) = является составным:

4294967297 = 641^.6700417.

Для бесконечного множества перебор невозможен и для доказательства истинности предложения (*) недостаточно проверить истинность Р(n) при n из какого-нибудь конкретного подмножества множества А. Более того, известны случаи, когда установление истинности Р(n) при всех n из достаточно широкого подмножества А₁ множества А приводили к неверной гипотезе о том, что утверждение (*) истинно.

П р и м е р 3. На сколько частей делит пространство n плоскостей, проходящих через одну точку так, что никакие три из них не проходят через одну прямую?

Одна плоскость делит пространство на две части. Две плоскости , проходящие через одну точку, делят пространство на

4-е части. Три плоскости, проходящие через одну точку, но не проходящие через одну прямую, делят пространство на 8 частей. Можно высказать утверждение , что для n = 1, n = 2, n = 3 число частей, на которое плоскости делят пространство равно 2ⁿ. Если сделать заключение, что n плоскостей разбивают пространство на 2ⁿ частей, то это предположение неверно.

П р и м е р 4. Рассмотрим ряд чисел вида b(n) = 991n² + 1.

Подставляя вместо n числа натурального ряда, начиная

с 1, мы не получим чисел, являющихся полным квадратом какого-либо другого числа, даже посвятив этому всю жизнь.

И все же математик не имеет право утверждать, что все числа указанного вида не являются квадратами. Это строго оправдано. В данном случае число b(n) = 991n² + 1 является полным квадратом при n = 12055735790331359447442538767.

П р и м е р 5. Пусть ( a_n ) - арифметическая прогрессия с

разностью d : a₁ = a₁; a₂ = a₁ + d; a₃ = a₂ + d = a₁ + 2d; a₄ = a₃ + d = = a₁ + 3d. Гипотеза: a_n = a₁ + (n -1)d.

Проверка при n = 1, 2, 3,...позволяет выдвигать гипотезу, которая нуждается в проверке, ибо гипотеза может быть верной или неверной. Индукция - сильное и опасное оружие: велико искушение принять указанную закономерность без строгого обоснования, ведь опыты так убедительны! Примеры 2, 3, 4, где гипотезы неверны, служат хорошим лекарством от такого искушения

Метод перебора является полноценным доказательством, но невозможен, если случаев бесконечно много. В последнем случае задачи часто решаются с помощью метода математической индукции.

ТЕОРЕМА (Принцип математической индукции)

Если на множестве натуральных чисел утверждение Р(n)

удовлетворяет условиям:

(а) P(1) истинно;

(б) (n)(P(n)  P(n+1)) истинно,

то истинно и предложение (n) P(n).

Справедливость принципа математической индукции следует из аксиом теории натуральных чисел. Более того, аналогичный принцип можно сформулировать и для высказывательной формы P(n) на множестве А, устроенном по типу множества натуральных чисел.

ОПРЕДЕЛЕНИЕ. Говорят, что множество А устроено по типу множества натуральных чисел, если его элементы можно упорядочить так, что

1) есть первый элемент а₁,

2) для каждого элемента а есть следующий за ним а^/,

3) каждый элемент из А можно получить как следующий за а₁ через конечное число шагов.

П р и м е р 6. А - множество четных неотрицательных чисел:

а₁ = 2, 2^/ = 4, 4^/ = 6 и т. д.

П р и м е р 7. А = N \  1, 2, 3 . a₁= 4, 4^/ = 5, 5^/ = 6, ...

П р и м е р 8. А = -n | n  N . a₁ = -1, (-1)^/ = -2, (-2)^/ = -3,

(-3)^/ = -4, ...

П р и м е р 9. A = Z. a₁= 0, 0^/ = 1, 1^/ = -1, (-1)^/ = 2, 2^/ = -2, (-2)^/ = 3, 3^/ = -4, ...

ТЕОРЕМА (Принцип математической индукции в более общей форме)

Пусть P(n) - высказывательная форма на множестве А устроенном по типу множества натуральных чисел такая, что

(а) Р(а₁) истинно;

(б) (n)(P(n)  P(n^/)) истинно,

тогда истинно и предложение (n) P(n).

На сформулированном принципе основан метод доказательства, называемый методом математической индукции. Доказательство уже сформулированных утверждений методом математической индукции разбивается на четыре части.

1. Проверка того, что доказываемое утверждение P(а₁) верно для первого элемента множества А. Эту часть доказательства называют базисом индукции.

2. Предположение, что доказываемое утверждение верно при некотором значении k  А. Индукционное предположение.

3. Доказательство того, что утверждение верно для следующего элемента из множества А, т.е. истинно Р(a^/). Индукционный шаг: P(k)  P(k+1).

4. Вывод: доказываемое утверждение истинно на основании принципа математической индукции.

Метод математической индукции применяется при решении задач на суммирование; задач, связанных с рекуррентным способом задания последовательности; при доказательстве тождеств и неравенств; выводе формул n-ого члена и суммы n первых членов арифметической и геометрической прогрессий; при решении задач на делимость и некоторые геометрические задачи, при доказательстве ряда математических утверждений и теорем.

Теоретические вопросы:

Принцип математической индукции. Различные формы метода математической индукции.

П р и м е р 11. Доказать, что число 7ⁿ⁺¹ + 8²ⁿ^-1 делится на 19 при любом натуральном n.

Решение.

1. Доказываемое утверждение верно при m = 1, так как 7² + 8¹ = 57 и 57 делится на 19.

2. Предположим, что данное утверждение верно при некотором значении m = k, где k  1, т.е. выражение р(k) = 7^k⁺¹ + 8²^k^-1 делится на 19.

3. С учетом сделанного предположения докажем, что выражение р(n) = 7ⁿ⁺¹ + 8²ⁿ^-1 делится на 19 при n = k + 1, т.е. 7^k⁺²+ 8²^k⁺¹ делится на 19.

Действительно, 7^k⁺²+ 8²^k⁺¹= 7^. 7^k⁺¹ + 64^. 8²^k^-1 = 7^. (7^k⁺¹ + 8²^k^-1) + + 57^.8²^k^-1. Каждое слагаемое полученной суммы делится на 19: первое по индукционному предположению и 57 делится на 19, поэтому и 7^k⁺²+ 8²^k⁺¹ также делится на 19.

4. На основании принципа математической индукции можно сделать вывод, что исходное выражение р(n) делится на 19 при любом натуральном значении n.

Условимся о следующем: если даны n чисел а₁, а₂, ... , а_n_,то вместо записи их суммы в виде а₁ + а₂ + ... + а_n_, мы будем использовать обозначение .

П р и м е р 2. Докажем, что для nN.

Решение

П е р в ы й с п о с о б. Обозначим данное утверждение через P(n), где nN. При п = 1 левая часть формулы принимает вид 1³,т.е. равна 1. Правая часть формулы при п = 1 принимает вид 1²(1+1)²/4 и тоже равна 1. Итак, Р(1) истинно.

Предположим, что это утверждение верно при п = k, т.е. что верно равенство .

Докажем, что P(k)  P(k+1) для k  N. Имеем:

1³ + 2³ +...+ k³ + (k +1)³ = = .

Итак, утверждение справедливо при п = 1, и из его справедливости для n = k следует, что оно верно и при n = k + 1. Значит, утверждение справедливо для любого натурального значения n.

В т о р о й с п о с о б. Введем обозначения:

А(n) = = 1³ + 2³ + 3³ + ... + n³; B(n) = . Надо доказать: (n  N) A(n) = B(n)

При n = 1: А(1) =1³ = 1, В(1) = , т.е. А(1) = В(1).

Пусть A(k) = B(k).

Докажем, что A(k+1) = B(k+1). Это утверждение будем доказывать в виде A(k+1) - A(k) = B(k+1) - B(k). Из последнего равенства с учетом того, что A(k) = B(k), получим A(k+1) = B(k+1).

A(k+1) - A(k) = ( 1³ + 2³ + ... + k³ + (k + 1)³) - ( 1³ + 2³ + ... + k³) = (k+1)³.

B(k+1) - B(k) = = = .

П р и м е р 3. Докажите, что при nN, n  5 справедливо неравенство 2ⁿ  n² + n + 2.

Решение

Обозначим данное утверждение через M(п). При п = 5 неравенство справедливо: 32  32.

Пусть M(к): 2^k  k² + k + 2 при n  5.

Докажем, что M(k)  M(k+1): 2^k⁺¹  (k + 1)² + (k + 1) + 2, т.е. 2^k⁺¹  k² + 3k + 4. Рассмотрим 2^k⁺¹ - k² - 3k - 4 = 2(2^k - k² - k - 2) + k² - k  0 на основании индукционного предположения и того, что k²- k  0 при n  5. На основании принципа математической индукции утверждение М(п) верно при n  5.