Лекція 11 Матриця густини та сприйнятливість ансамбля атомів

11.1. Матриця густини

Для обрахунку фізичних величин квантових систем, що складаються з багатьох частинок (лазерне активне середовище) використовують матрицю густини. Нехай ансамбль складається з частинок, кожна з яких описується нормованою хвильовою функцією . Введемо набір ортонормованих власних функцій і розкладемо по них хвильові функції.

(11.1)

Розглянемо деяку фізичну величину , що характерезує систему і спробуємо знайти її значення у випадку ансамблю систем. Для кожного з членів ансамбля середня величина знаходиться по відомій хвильовій функції з допомогою формули:

(11.2)

Таке визначення середнього значення є наслідком статистичного характеру опису засобами квантової механіки. Якщо тепер провести усереднення по всьому ансамблю, то ми отримаємо очікуване значення спостережуваної величини для системи, що розглядаємо.

(11.3)

де

Поміняємо порядок сумування в формулі (11.3) і введемо матрицю густини, елементи якої ми визначимо наступним чином:

(11.4)

відмітимо, що порядок розміщення нижніх індексів в лівій частині зворотній в порівнянні з правою.

Тепер ми можемо представити (11.3) у вигляді:

(11.5)

або в матричній формі З визначення (11.5) видно, що матриця – ермітова

(11.6)

а також нормована на одиницю:

(11.7)

Для того, щоб вивести рівняння руху для матриці густини, допустимо, що хаильова функція атомів в ансамблі задовільняє рівнянню Шредінгера:

,

і може бути розкладена в ряд по власних функціях, що складають повний ортонормований набір:. Тут ми індекс поміняли на внаслідок отримаємо:

Помножимо останнє рівняння на та проінтегруємо по всьому об’єму, внаслідок отримаємо:

або

(11.8)

де

Через те, що оператор є ермітовий, можемо написати:

(11.9)

Помноживши (11.8) на , а (11.9) на і результати додамо, будемо мати:

Останній вираз усереднимо по ансамблю частинок (сума від до ):

або:, або в матричній формі:

(11.10)

де квадратні дужки і кома означають коммутатор.

11.2. Сприйнятливість ансамбля атомів

В цій лекції формалізм матриці густини буде використаний при виведені виразу для сприйнятливості ансамбля атомів, що взаємодіють з електромагнітним полем, яке гармонічно міняється в часі. Допустимо, що у взаємодії беруть участь тільки два рівні з енергіями і , як показано на рис. 11.1.

Рис. 11.1. Дворівнева атомна система, яка взаємодіє з електромагнітним полем випромінювання, частота якого Передбачається, що всі інші нерезонансні рівні (вони позначені штрихованими лініями) безпосередньо у взаємодії не беруть участіЖ їх присутність впливає на рівноважне значення населеності рівнів і .

Таке допущення можливе, коли частота ЕМ – поля задовільняє умові В цьому випадку матриця густини зводиться до матриці розміром з елементами Допустимо, щомає місце електродипольна взаємодія, якому вілповідає гамільтоніан:

(11.11)

де – паралельна полю компонента оператора дипольного моменту. Будемо покb вважати поле класичною змінною. Отже для оператора можемо написати:

(11.12)

Дальше ми будемо опускати дашок над операторами. Отже а

(11.13)

Діагональні елементи оператора рівні нулю: оскільки стани 1 і 2 володіють певною парністю (або обидва парні або обидва непарні). Фази власних функцій стану 1 і 2 можна вибрати так, Отже

Потрібно знайти середнє по ансамблю значення дипольного моменту атома , наведеного полем . У відповідністю з формулою (11.5):

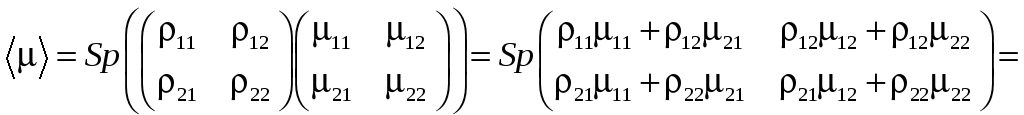
(11.14)

Отже Матриця густини записується у представлені незбуреного оператора так, що базисні функції задовільняють рівнянню

Н₀_n =  _n _n . Для визначення потрібно розрахувати і . Отже виразів (11.12) і (11.13) отримуємо:

(11.15)

тому що . (11.16)

З умови нормування

(11.17)

(11.18)

(11.19)

(11.20)

Зверномося до рівняння (11.15). Після виключення збуреного поля величина повинна прямувати до нуля, оскільки фазова когерентність між власними функціями ансамбля виражається через удари (зіткнення) між членами ансамбля. В результаті буде релаксувати з часом. Такі зіткнення визначають ширину спектральних ліній, як було показано в лекції 9. Щоб включити в розгляд явище втрату фазової когерентності (зіткнення між частинками) рівняння (11.20) необхідно доповнити релаксаційним членом:

(11.21)

Дипольний момент матриці густини дає ймовірність знаходження атома в і – му стані. Якщо – густина атомів, то — (середня) густина різниці населеностей між двома рівнями. Позначимо рівноважне (при ) значення через і допустимо, що коли виключено, різниця населеностей релаксує до рівноважного значення з постійною часу Отже, (11.19) можна написати у вигляді:

(11.22)

Розглянемо тепер частковий випадок, коли з часом міняється по гармонічному закону.

(11.23)

З (11.22) випливає, що для незбуреної системи () зручно користуватися новими повільно змінними і які вводяться співвідношенями:

. (11.24)

Підставимо (11.23) і (11.24) в рівняння (11.21) і (11.22), будемо мати:

(11.25)

(11.26)

При виведенні формули (14.25) зберігалися тільки члени, що мають часову залежність а при отриманні (11.26) — лише такі члени, що не мають експоненціальної залежності від часу, таким чином опущені доданки з часовою залежністю і . Нехтування несинхронними членами виправдано тому, що в середньому їх вклад за період рівний нулю. Якщо підставити (11.24) в (11.14), то отримаємо: а завдяки тому, що то можна написати:

(11.27)

Щоб знайти матрицю густини стаціонарного стану прирівняємо ліві частини рівнянь (11.25) і (11.26) до нуля . Будемо мати:

(11.28)

(11.29)

.

Підставляємо останню рівність в друге рівняння (11.29), будемо мати:

З останнього рівняння можна визначити

(11.30)

Напишемо до рівняння (11.28) комплексно спряжене:

(11.31)

Спочатку додамо рівняння (11.28) і (11.31), будемо мати:

(11.32)

Від рівняння (11.28) віднімемо (11.31), отримаємо:

(11.33)

З (11.32) визначимо і підставляємо в (11.33). З (11.30) визначаємо і підставляємо в (11.33):

(11.34)

(11.34)

(11.35)

Маючи (11.35) можна визначити з (11.32):

(11.36)

В формулах (11.35) і (11.36) частота нутації З (11.35) підставляємо в (11.30), будемо мати:

(11.37)

Макроскопічна (змінна) поляризація у відповідності (11.27) отримуємо:

(11.38)

. (11.39)

Тоді різниця населеностй в одиниці об’ємуна основі виразу (11.37):

, (11.40)

де – різниця населеностей у відсутності поля.

Якщо скористатися позначенням спприйнятливості , то

(11.41)

то порівнявши (11.41) з (11.39), отримаємо:

(11.42)

Введемо в розгляд нормовану функцію форми лінії

(11.42а)

де – ширина на рівні половини від максимуму.

Очевидно, що функція пропорційна поглинанню, – зміні показника заломлення під впливом накачування, отже: Вид цих функцій представлений на рис. 11.2.

Рис.11.2 Дійсна () і уявна () частини сприйнятливості при нехтуванні насиченням

Функція , що визначена за формулою (11.42) описує нормовану лоренцеву форму лінії. Постійна нормування знаходиться з умови