3.2.4.2Особенности арифметика чисел с плавающей запятой

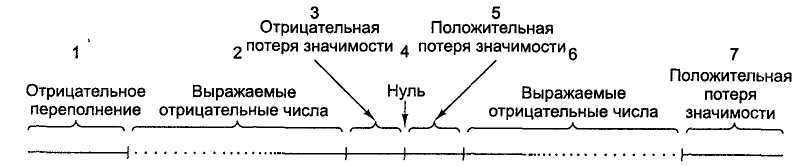
Числа с плавающей точкой можно использовать для моделирования системы действительных чисел в математике, хотя здесь есть несколько существенных различий. На рисунке представлена ось действительных чисел, для представления которых используется 1 байт (см. предыдущий пункт).

Первое отличие действительных чисел от чисел с плавающей точкой, которые представляются 1 байтом, состоит в том, что последние нельзя использовать для записи чисел из областей 1, 3, 5 и 7. Если в результате арифметической операции получится число из области 1 или 7, то произойдет ошибка переполнения и резуль­тат будет неверным. Причина – ограничение области значений чисел в данном представлении. Точно так же нельзя выразить результат из области 3 или 5. Такая ситуация называется ошибкой из-за потери значимости. Эта ошибка менее серь­езна, чем ошибка переполнения, поскольку часто нуль является вполне удовле­творительным приближением для чисел из областей 3 или 5.

Второе важное отличие чисел с плавающей запятой от действительных чисел ­ это их плотность. Между любыми двумя действительными числами х и у существу­ет другое действительное число независимо от того, насколько близко к у располо­жен х. Действи­тельные числа формируют континуум.

Числа с плавающей точкой континуума не формируют. В рассмотренной выше системе представления можно выразить лишь конечное количество действительных чисел. Если полученное число нельзя выразить в используемой системе представления, нужно брать ближайшее число, которое представимо в этой систе­ме. Такой процесс называется округлением. (см. рисунок)

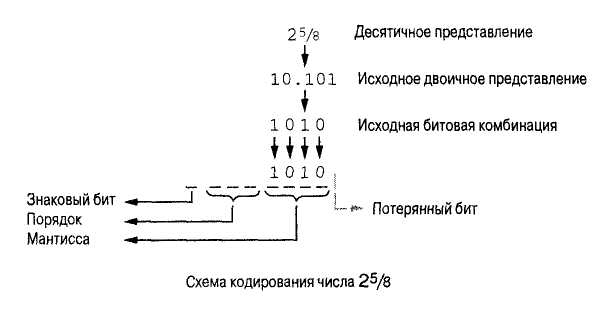
Промежутки между смежными числами, которые можно выразить в представле­нии с плавающей запятой, во второй и шестой областях не постоянны. Однако если промежутки между числом и его соседом выразить как процентное отношение от этого числа, большой разницы в проме­жутках не будет. Другими словами, относительная погрешность, полученная при округлении, приблизительно равна и для малых, и для больших чисел.

3.2.4.3Стандарт ieee 754.

До 80-х годов каждый производитель имел свой собственный формат чисел с пла­вающей точкой. Все они отличались друг от друга. Более того, в некоторых из них арифметические действия выполнялись неправильно, поскольку арифметика с плавающей точкой имеет некоторые тонкости, которые не очевидны для обыч­ного разработчика аппаратного обеспечения.

Чтобы изменить эту ситуацию, в конце 70-х годов IEEE учредил комиссию для стандартизации арифметики с плавающей точкой. Целью было не только дать воз­можность переносить данные с одного компьютера на другой, но и обеспечить раз­работчиков аппаратного обеспечения заведомо правильной моделью. В результа­те получился стандарт IEEE 754 (IEEE, 1985).

Стандарт определяет три формата: с одинарной точностью (32 бита), с удвоен­ной точностью (64 бита) и с повышенной точностью (80 битов).

1. 32 разряда. Для представления чисел используются 8 разрядов для показателя степени и 24 разрядов для мантиссы. Описанный формат дает числа в диапазоне примерно 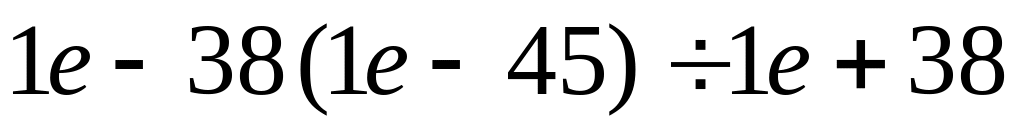с 7-8 десятичными знаками точности.

2. 64 разряда. Для представления чисел используется 11 разрядов для показателя степени и 53 разряда для мантиссы. Описанный формат дает числа в интервале примерно 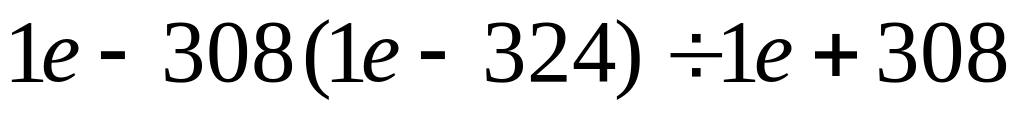с 15-16 десятичными знаками точности.

3. 80 разрядов. Для представления чисел используется 17 разрядов для показателя степени и 63 разряда для мантиссы. Описанный формат дает числа в интервале примерно 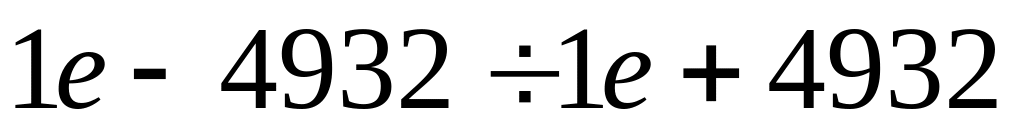с 19-20 десятичными знаками точности.

Рассмотрим более подробно форматы с одинарной и удвоенной точностью

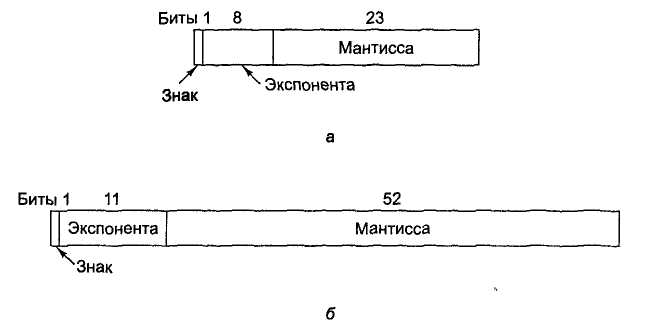
Числовые характеристики стандарта IEEE для чисел с плавающей точкой даны в таблице

Параметр	Одинарная точность	Удвоенная точность
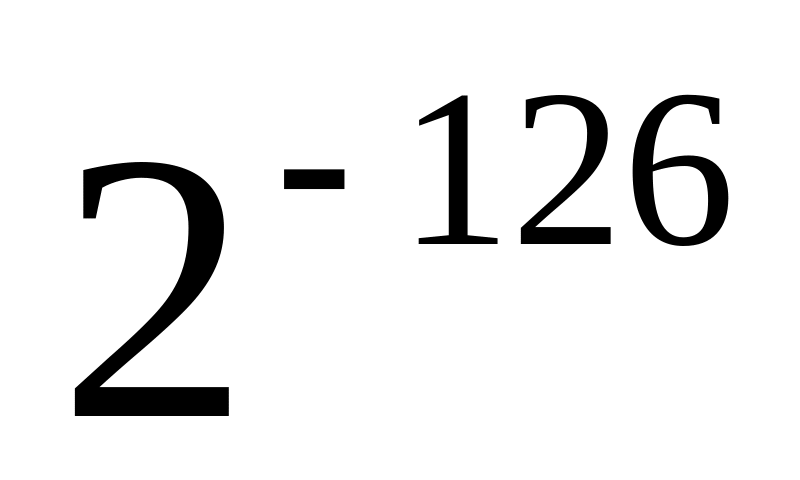
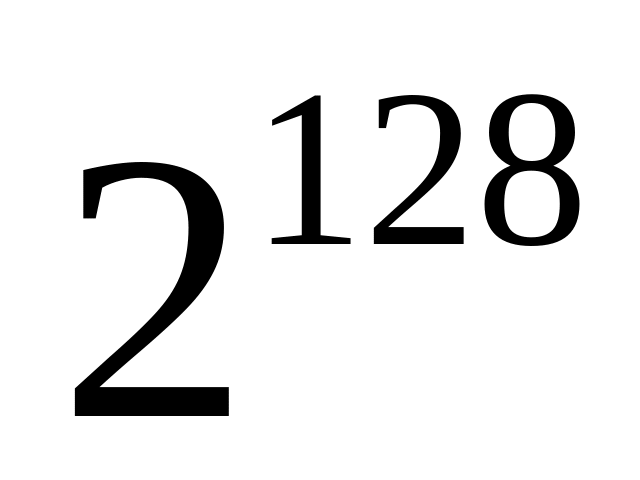
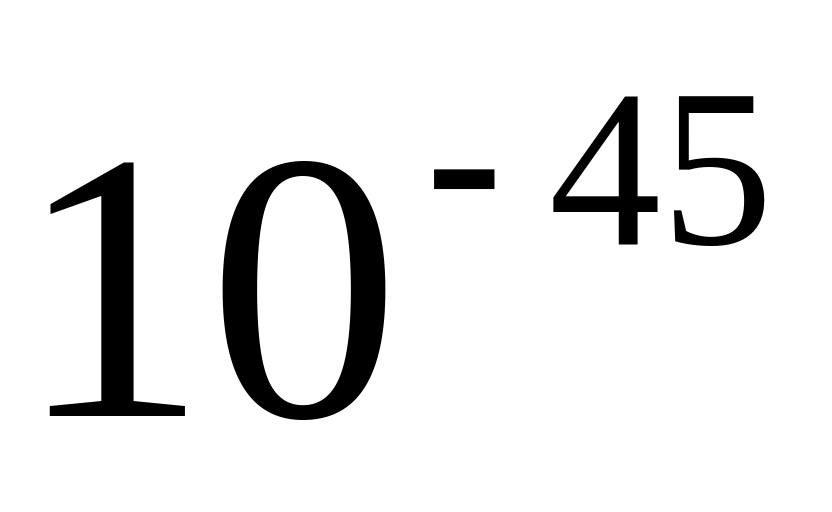
Количество битов в знаке Количество битов в экспоненте Количество битов в мантиссе Общее число битов Смещение экспоненты Область значений экспоненты Самое маленькое нормализованное число Самое большое нормализованное число Диапазон десятичных дробей Самое маленькое ненормализованное число	1 8 23 32 Смещение (excess) 127 От-126 до+127	1 11 52 64 Смещение (excess) 1023 От-1022 до+1023

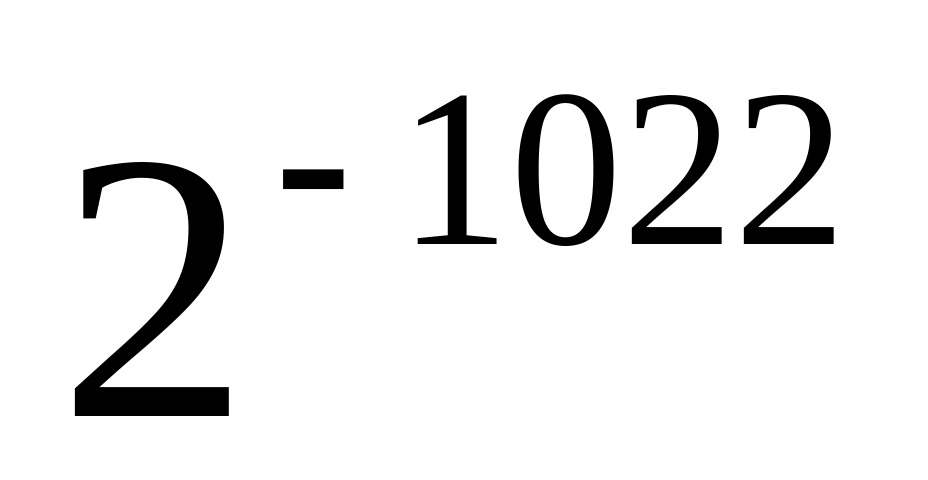
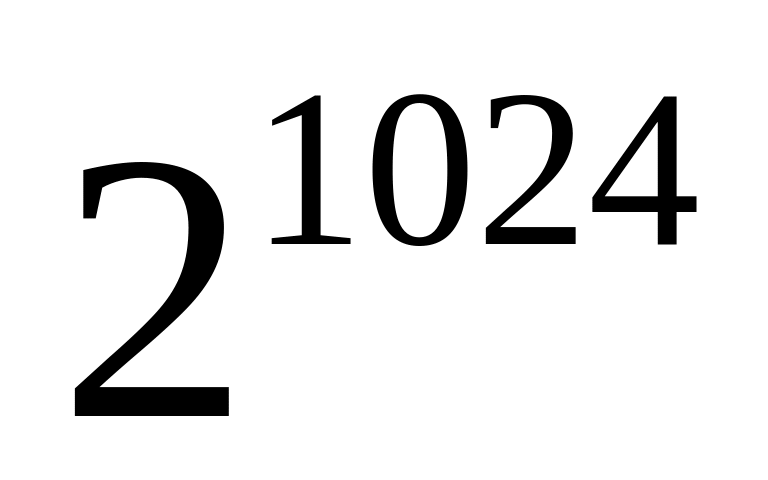
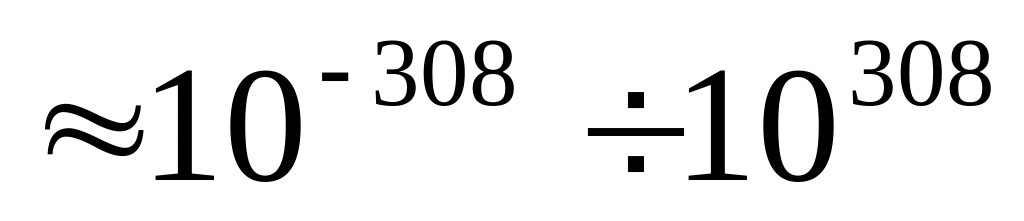
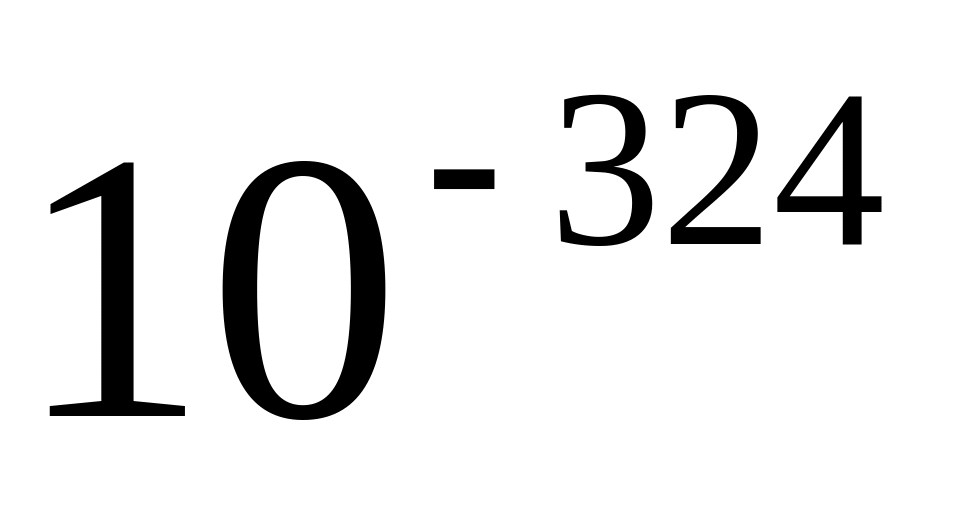
Традиционные проблемы, связанные с числами с плавающей точкой, – что делать с переполнением, потерей значимости и неинициализированными числа­ми.

Проблема возникает в том случае, если абсолютное значение (модуль) резуль­тата меньше самого маленького нормализованного числа с плавающей точкой, ко­торое можно представить в этой системе. Раньше аппаратное обеспечение действо­вало одним из двух способов: либо устанавливало результат на 0, либо вызывало ошибку из-за потери значимости. Ни один из этих двух способов не является удов­летворительным, поэтому в стандарт IEEE введены ненормализованные числа.

Рис. Числовые типы стандарта IEEE

Самое маленькое нормализованное число с одинарной точностью содержит 1 в экспоненте и 0 в мантиссе и представляет . Самое большое ненорма­лизованное число содержит 0 в экспоненте и все единицы в мантиссе и представ­ляет примерно , то есть почти то же самое число. Следует отметить, что это число содержит только 23 бита значимости, а все нормализованные чис­ла – 24 бита.

По мере уменьшения результата при дальнейших вычислениях экспонента по-прежнему остается равной 0, а первые несколько битов мантиссы превращаются в нули, что сокращает и значение, и число значимых битов мантиссы. Самое малень­кое ненулевое ненормализованное содержит 1 в крайнем правом бите, а все ос­тальные биты равны 0. Экспонента представляет , а мантисса­ – , поэтому значение равно . Такая схема предусматривает постепенное исчезновение зна­чимых разрядов, а не перескакивает на 0, когда результат нельзя выразить в виде нормализованного числа.

В этой схеме присутствуют 2 нуля, положительный и отрицательный, опреде­ляемые по знаковому биту. Оба имеют экспоненту 0 и мантиссу 0. Здесь тоже бит слева от двоичной запятой по умолчанию 0, а не 1.

С переполнением нельзя справиться постепенно. Вместо этого существует спе­циальное представление бесконечности: с экспонентой, содержащей все единицы, и мантиссой, равной 0. Это число можно использовать в качестве операнда. Оно подчиняется обычным математическим правилам для бесконечности.

А что получится, если бесконечность разделить на бесконечность? Результат не определен. Для такого случая существует другой специальный формат, NaN (Not a Number — не число). Его тоже можно использовать в качестве операнда.