Предельный переход в неравенствах

Теорема 1. Пусть - сходящаяся последовательность и . Тогда .

Доказательство этой теоремы проведем методом от противного.

Обозначим . Тогда утверждение, противоположное доказываемому, имеет вид:

.

Возьмем . Тогда, по определению, предела последовательности, можно написать

.

Последнее неравенство распишем в виде двойного

Но так как , то и получается что , что противоречит условию теоремы.

Следствие. Если и сходящиеся последовательности и , то

.

Доказательство дается следующей цепочкой следствий

=> => =>

=>

Важное замечание. Допустим, что в условии теоремы вместо мы написали . Можно ли утверждать, что ?

Ответ отрицательный. Действительно, пусть, например, . Тогда , но .

Таким образом, итог этой теоремы и замечание выглядит так: в неравенствах допустим предельный переход, надо только иметь ввиду, что после предельного перехода строгое неравенство (типа > или <) может замениться на нестрогое

(> перейдет в , < перейдет в ).

Вопрос 22: Предел функции. Определение предела функции в точке. Предел функции при х→∞. Односторонние пределы.

Преде́л фу́нкции (предельное значение функции) в заданной точке, предельной для области определения функции, — такая величина, к которой стремится рассматриваемая функция при стремлении её аргумента к данной точке.

Определение. Число А называется пределом числовой последовательности {an}, если для любого даже сколь угодно малого положительного числа ε>0 найдется такой номер N( зависящий от ε), N = N(ε), что для всех членов последовательности с номерами n>N верно неравенство: |an - A| < ε

lim = A

n→∞

Опр: Число А называется пределом функции у = f(х) при Х→Хо, если для любого сколько угодно малого, но положительного числа ε найдется такое положительное число , что для всех Х выполняется условие:

Хо – 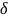< Х < Хо + δ

lim = A

n→∞

Односторо́нний преде́л в— предел числовой функции, подразумевающий «приближение» к предельной точке с одной стороны. Такие пределы называют соответственно левосторо́нним преде́лом (или преде́лом сле́ва) и правосторо́нним преде́лом (или преде́лом спра́ва).

Вопрос 23: Основные теоремы о пределах: единственность предела функции, пределы функций f(X) g(X), f(X)·g(X), f(X)/g(X), c·f(X).

Теорема о единственности предела:

Если последовательность имеет предел, то он единственен.

1 f(x) g(x) → 0 - сумма и разность бмв и есть бмв.

2. f(x)·g(x)→0 – произведение бмв и есть бмв.

3. f(x)/g(x) →0 – отношение бмв есть бмв, const

4. c·f(x) →0 – произведение const и бмв есть бмв.

Вопрос 24: Бесконечно малые и бесконечно большие функции. Аривметические операции над бесконечно малыми функциями.

Опр 1: Переменная величина Хn называется бесконечно малой, если для всякого наперед заданного положительного числа ε можно узнать такое натуральное число N, что |Xn|<ε, для всех n>N.

Опр 2: Если {n имеет предел О, т.е.

lim Хn = 0, то такая величина на называется бесконечно малой величиной.

х→0

Опр 1: Величина Xn называется бесконечно большой, если для любого наперед заданного числа М>0 можно указать такое натуральное число N, что для всех номеров n>N выполняется неравенство |Xn|>M.

Свойства бмв:

1 f(x) g(x) → 0 - сумма и разность бмв и есть бмв.

2. f(x)·g(x)→0 – произведение бмв и есть бмв.

3. f(x)/g(x) →0 – отношение бмв есть бмв, const

4. c·f(x) →0 – произведение const и бмв есть бмв.

Свойства ббв:

1 f(x) g(x) → ∞

2. f(x)·g(x)→∞

3. f(x)/g(x) →∞ –бмв, ббв, const

4. c·f(x) →∞