Вопрос 60.Формула Ньютона-Лейбница .

Формула (1) называется формулой Ньютона — Лейбница. Она верна для любой функции f, непрерывной на отрезке [а; b]

Вопрос 61. Интегрирование заменой переменной.

Формула (22) выражает собой правило замены переменной в определенном интеграле. Оно напоминает правило замены переменной в интеграле неопределенном, но отличается от него тем, что здесь отпадает надобность в возвращении к старой переменной, т. к. формула (22) представляет собой равенство двух постоянных чисел. Заметим еще, что эта формула заменяет собой для случая определенных интегралов оба вида правила подстановки в интегралах неопределенных; только, применяя ее на практике, иной раз приходится читать ее слева направо, а иногда - справа налево.

Вопрос 62 Интегрирование по частям определенного интеграла.

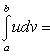
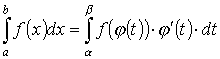
Если функции u=u(x) и v=u(x) имеют непрерывные производные на отрезке на отрезке [а; b].

Вопрос 63. Несобственные интегралы с бесконечными пределами интегрирования.

Определение. Пусть функция 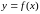определена и непрерывна на промежутке 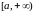, тогда

(12)

называется несобственным интегралом с бесконечным верхним пределом интегрирования (несобственным интегралом I рода).

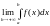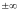Если существует и конечен, то несобственный интеграл называется сходящимся; если данный предел не существует или равен , то несобственный интеграл называется расходящимся.

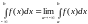
Несобственный интеграл с двумя бесконечными пределами интегрирования определяется следующим образом:

Вопрос 64. Несобственные интегралы от неограниченных функций

Определение. Несоб.интг.2 рода--.это интеграл по конечному интегрированию от функций не ограниченных в конечном числе точек.

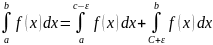
Если функция имеет бесконечный разрыв в точке x=c, c [а; b]. и непрерывна во всех точках этого отрезка, то 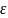=б.м.в

Если функция терпит разрыв в нижнем пределе, то

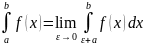
Если функция терпит разрыв в верхнем пределе, то

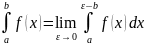
Вопрос 65.Вычисление площадей плоских фигур

1)Как уже было установлено (см. «геометрический смысл определенного интеграла»), площадь криволинейной трапеции, расположенной «выше» оси абсцисс (ƒ(х) ≥ 0), равна соответствующему определенному интегралу:

2)Отметим,что если криволинейная трапеция расположена «ниже» оси Ох (ƒ(х) < 0), то ее площадь может быть найдена по формуле

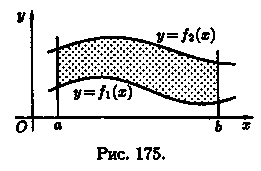
3)Площадь фигуры, ограниченной кривыми у =  = fι(x) и у = ƒг(х), прямыми х = а и х = b (при условии ƒ₂(х) ≥ ƒ₁(х)) (см. рис. 175), можно найти по формуле

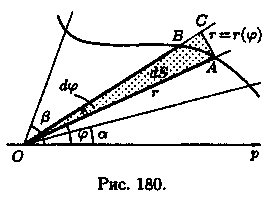
4)Найдем площадь S криволинейного сектора, т. е. плоской фигуры, ограниченной непрерывной линией r=r(φ) и двумя лучами φ=а и φ=β (а < β), где r и φ — полярные координаты (см. рис. 180). Для решения задачи используем схему II — метод дифференциала.

1. Будем считать часть искомой площади S как функцию угла φ, т. е. S = S(φ), где а ≤φ≤β (если φ = а, то S(a) = 0, если φ=β, то S(β) = S).

2. Если текущий полярный угол φ получит приращение Δφ = dφ, то приращение площади AS равно площади «элементарного криволинейного сектора» OAB.

Дифференциал dS представляет собой главную часть приращения ΔS при dφ→0 и равен площади кругового сектора О АС (на рисунке она  заштрихована) радиуса r с центральным углом dφ. Поэтому

3. Интегрируя полученное равенство в пределах от φ = а до φ = β, получим искомую площадь

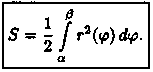
5)И, наконец, если криволинейная трапеция ограничена кривой, заданной параметрически

прямыми х = аих = bи осью Ох, то площадь ее находится по формуле