1.4 Поняття про скінченні різниці

Якщо ряд Тейлора для функції f(x):

f(x+h)=f(x)+f’(x)h+(fⁿ(x)/2!)*h²+…

обірвати на другому члені, то можна отримати праву різницеву похідну.

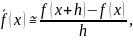(1)

яка апроксимує першу похідну f’(x) в точці х.

В розкладанні Тейлора функції f(x) можна замінити h на –h й отримати ліву різницеву похідну.

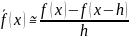(2)

Додаючи (2) до (1) маємо центральну різницеву похідну:

Якщо в ряді Тейлора залишити ще один доданок, то аналогічним шляхом можна отримати центральну різницеву похідну для апроксимації f’’(x):

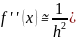
Тепер можна поширити поняття скінченно-різницевої апроксимації на часткові похідні. Якщо виходити з розкладання Тейлора функції двох змінних

u(x+h,y)=u(x,y)+u_x(x,y)*h+u_xx(x,y) (h²/2!)+…

u(x-h,y)=u(x,y)-u_x(x,y)*h+u_xx(x,y) (h²/2!)-…

то можна отримати наступні апроксимації часткових похідних

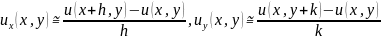
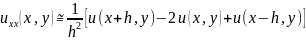
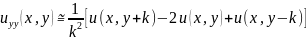
2. Параболічні рівняння

2.1 Задача електропровідності

Математична модель електропровідності потребує трьох типів співвідношень:

1. РЧП, котре описує фізичне явище електропровідності;

2. Граничних умов, які характеризують електричну напругу на границях розглядуваної області;

3. Початкових умов, котрі задають електричну напругу на початку процесу у всіх точках області.

Одновимірне рівняння електропровідності

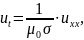(2.1)

де μ₀=4π*10^-7Гн/м – магнітна проникність, σ – питома електрична провідність провідника довжиною L [0,L].

Одновимірне рівняння електропровідності пов’язує електричний струм і вогнутість напруги U_xx (вогнутість є мірою відмінності напруги у певній точці від напруги у сусідніх точках).

Якщо вогнутість апроксимувати скінченними різницями

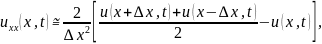
то можна дати таку інтерпретацію (рис. 1).

1. Якщо напруга u(x,t) менша середнього значення напруги в сусідніх точках, то U_xx>0 (струм додатний);

2. Якщо напруга u(x) дорівнює середньому значенню напруги в сусідніх точках, то U_xx=0 (струм нульовий);

3. Якщо напруга u(x,t) більша середнього значення напруги в сусідніх точках, то U_xx<0 (струм від’ємний).

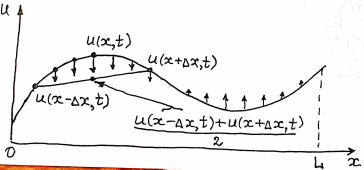
Рис 1. Приклад профілю напруги у момент часу t.

Якщо вігнутість апроксимувати скінченними різницями, то можна дати таку інтерпретацію: якщо напруга U(x,t) менша середнього значення напруги у сусідніх точках, то U_xx>0

Якщо напруга U(x,t)= середньому значенню напруги у сусідніх точках, то U_xx=0

Якщо напруга U(x,t)>середнього значення напруги у сусідніх точках, то U_xx<0

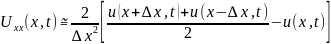
Граничні умови властиві для всіх задач математичної фізики, оскільки процес відбувається у певній частині простору. Оскільки напруга на кінцях провідника підтримується постійною, то граничні умови можна записати так:

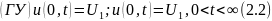
Початкові умови характеризують стан процесу у момент початку, котрий, як правило вважається нульовим (t=0). У нашій задачі дослідження напруги почалося, коли провідник володів постійною напругою U₀, то

u(x,0)=U₀, 0≤x≤L (2.3)

З метою чисельного розв’язування цієї задачі методом скінченних різниць побудуємо прямокутну сітку, вузли котрої визначаються формулами:

x_j=jh (j=0,1…,n)

t_j=ik (i=0,1,…,m)

Замінимо часткові похідні їхніми скінченно-різницевими апроксимаціями

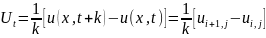
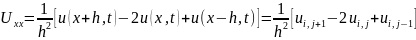
Підставимо ці вирази в рівняння (2.1) й розв’яжемо отримане рівняння відносно значень функції для наступного часового шару.

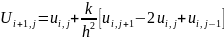(2.4)

Оскільки з граничних і початкових умов відомі значення U_ij на лівій і нижній сторонах сітки (рис.2), то потрібно знайти решту значень U_ij за явною схемою поточного обчислення при t=∆t, 2∆t, 3∆t, … , коли розв’язок у поточний момент часу подається через розв’язок у попередній момент за допомогою формули (2.4). На рис. 2 виділено приклад сукупності значень U_ij, котрі утворюють типовий обчислювальний шаблон.

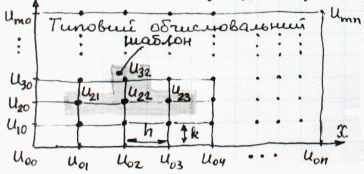
Рис 2. Сітка для рівняння електропровідності

Заштрихована частина – типовий обчислювальний шаблон

Замінимо часткові похідні їхніми скінченно-різницевими апроксимаціями

(*)

Підставимо ці вирази у рівняння 1 та розв’яжемо останнє рівняння відносно значень функції для наступного часового шару. У шаблоні і = 2, j = 2.

Оскільки з граничних та початкових умов відомі значення іj на лівій та нижній сторонах сітки, то потрібно знайти решту значень U_ij за явною схемою поточного обчислення при t=delta t, 2 delta t,3 delta t … .

Коли розв’язок у поточний момент часу подається через розв’язки в попередні моменти за допомогою формули (*) виділено приклад сукупності значень для типового шаблону.

Суттєвий недолік даної схеми такий: якщо часовий крок достатньо великий у порівнянні з кроком dx, похибки округлення виявляються настільки значними, що отриманий розв’язок втрачає сенс. Відношення кроків для t та х залежать від рівняння і граничних умов але достатньо виконання нерівності k/h²<=0,5.

Суттєвий недолік явної схеми такий. Якщо часовий крок достатньо великий у порівнянні з кроком для х, похибки округлення виявляються настільки значними, що отриманий розв’язок утрачає сенс. Відношення кроків для t й х залежить від рівняння й граничних умов, але достатньо виконання умови:

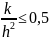
Справедливе таке емпіричне правило: якщо зменшувати кроки ∆t і ∆х, то похибка апроксимації часткових похідних скінченними різницями теж зменшується однак чим дрібніша сітка, тим більший обсяг обчислень слід виконати, а тому більшими будуть похибки округлення.

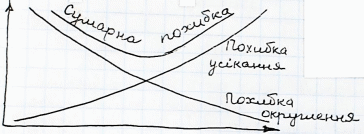
Графік 1. Залежність похибки від кроку сітки

Якщо крок сітки вздовж осі Х обрати ∆X=0,1, то часовий крок не може бути більшим ніж

0,5x(0,1)²≤∆t ∆t=0,005

Це означає, що від t=0 до t=1 можна дійти за допомогою 200 кроків.