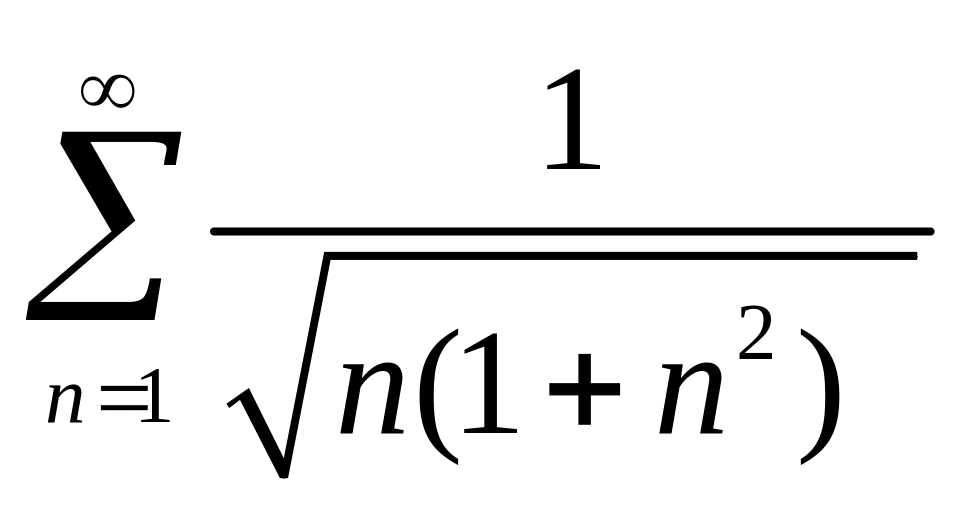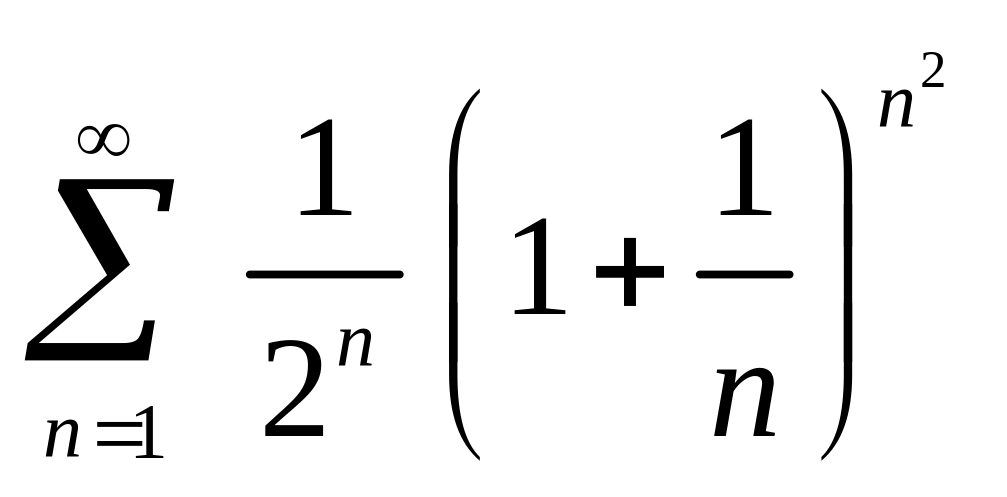- •Н.С.Распопова – Математический анализ. Часть 2. Общие методические указания
- •Литература
- •Задания для контрольной работы
- •1. Вычислить неопределенные интегралы
- •2. Вычислить интегралы по формуле Ньютона-Лейбница
- •3. Вычислить несобственный интеграл или установить его расходимость
- •4. Исследовать ряд на сходимость.
- •Методические указания к решению задач неопределенные интегралы и их свойства
- •Свойства неопределенного интеграла
- •Внесение под знак дифференциала
- •Вычисление интегралов, содержащих квадратный трехчлен
- •Интегрирование рациональных дробей
- •Интегрирование по частям
- •Вычисление определенных интегралов. Формула ньютона-лейбница
- •Замена переменных
- •Несобственные интегралы
- •Числовые ряды
- •Необходимый признак сходимости
- •Признак даламбера
- •Радикальный признак коши
- •Интегральный признак коши
- •Признак сравнения
- •Предельный признак сравнения
- •Содержание
4. Исследовать ряд на сходимость.
Вариант 1. |
Вариант 2. |
|
|
Вариант 3. |
Вариант 4. |
|
|
Вариант 5. |
Вариант 6. |
|
|
Вариант 7. |
Вариант 8. |
|
|
Вариант 9. |
Вариант 10. |
|
|
Вариант 11. |
Вариант 12. |
|
|
Вариант 13. |
Вариант 14. |
|
|
Вариант 15. |
Вариант 16. |
|
|
Вариант 17. |
Вариант 18. |
|
|
Вариант 19. |
Вариант 20. |
|
|
Вариант 21. |
Вариант 22. |
|
|
Вариант 23. |
Вариант 24. |
|
|
Вариант 25. |
Вариант 26. |
|
|
Вариант 27. |
Вариант 28. |
|
|
Вариант 29. |
Вариант 30. |
|
|
Методические указания к решению задач неопределенные интегралы и их свойства
Функция F(x) называется первообразной для функции f(x), если
![]()
Можно показать, что все первообразные для функции f(x) отличаются друг от друга на постоянное слагаемое, т.е. все первообразные можно записать в виде F(x) + C, где C – произвольная постоянная. Совокупность всех первообразных для функции f(x) называется неопределённым интегралом и обозначается следующим образом:
![]() .
.
При этом f(x) называется подынтегральной функцией.
Свойства неопределенного интеграла
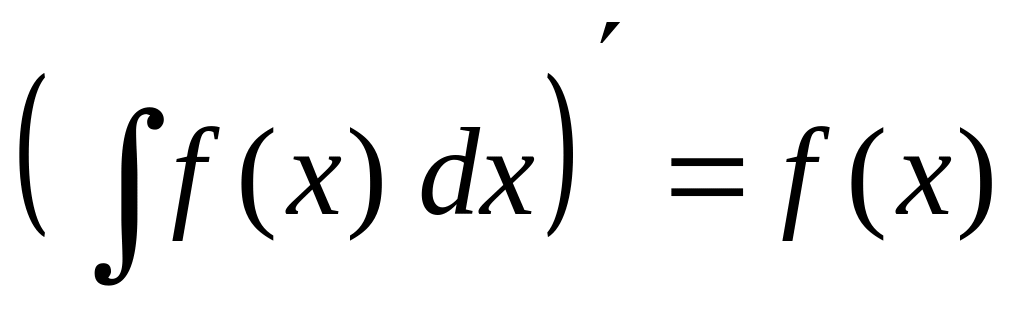 .
.
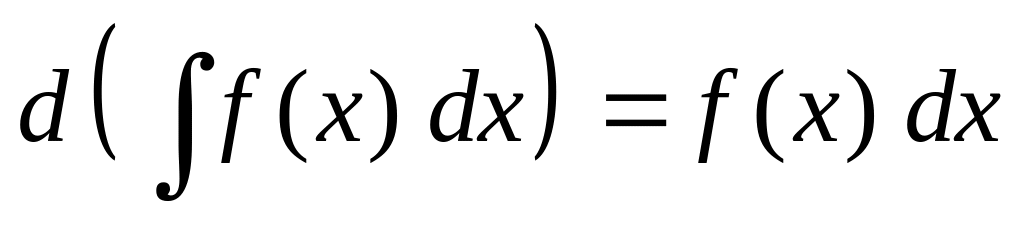 .
.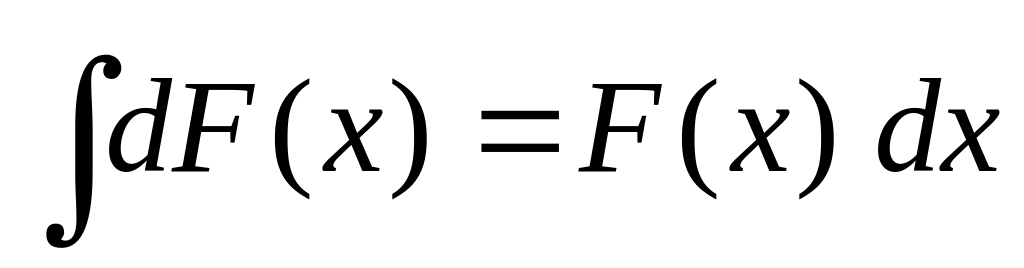 .
.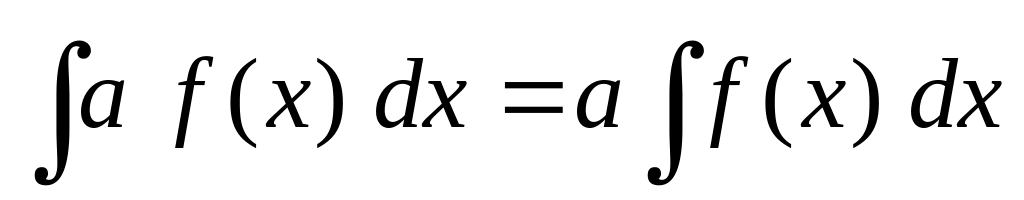 .
.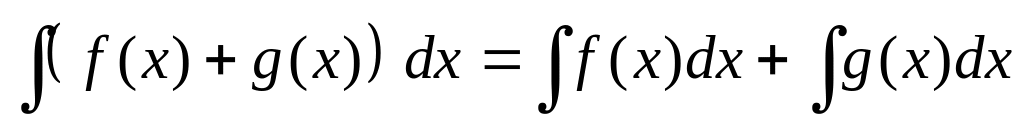 .
.Если
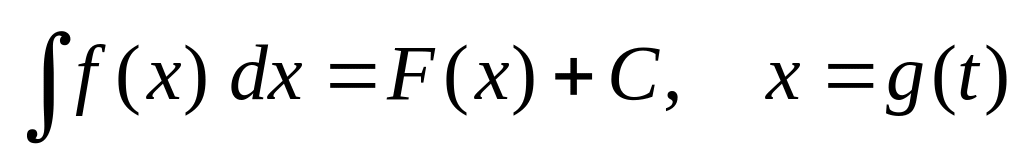 ,
то
,
то
![]() .
.
ТАБЛИЦА ИНТЕГРАЛОВ.
1 )
)![]() .
.
2)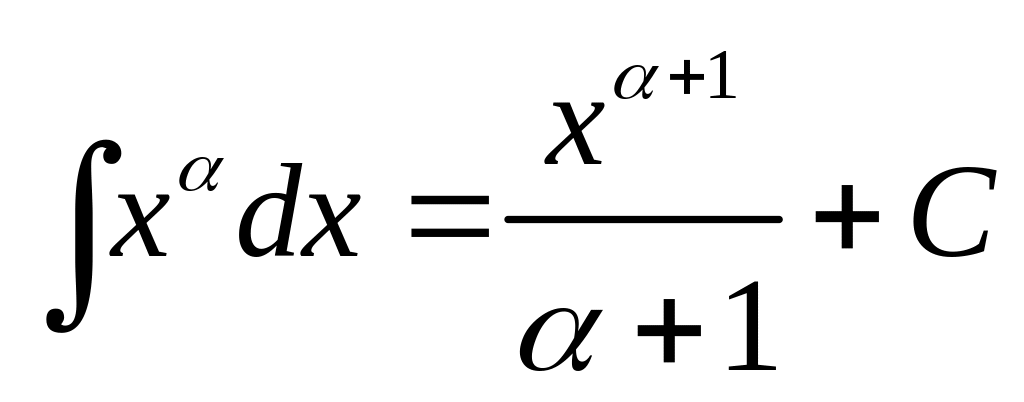 ,
если α ≠ -1. Напомним, что
,
если α ≠ -1. Напомним, что
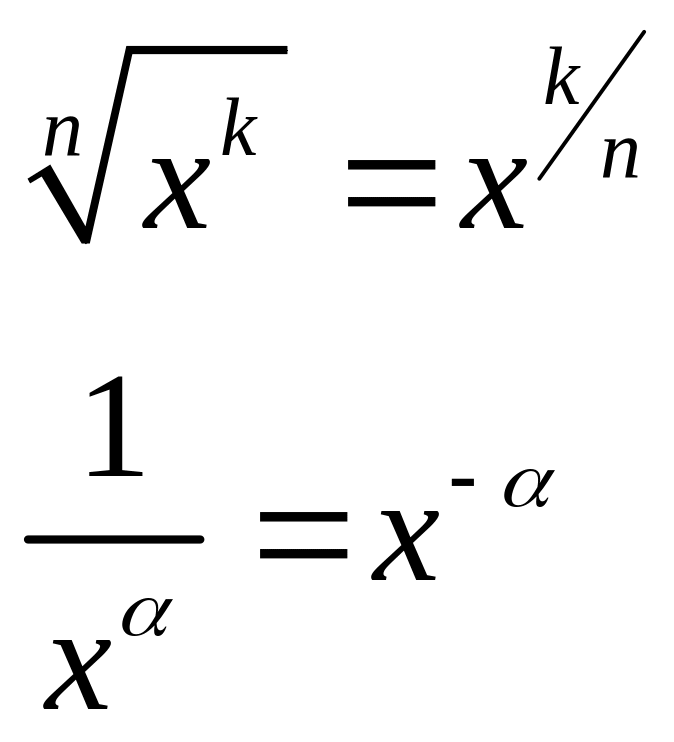 .
.
3)![]() .
.
4)![]() .
.
5)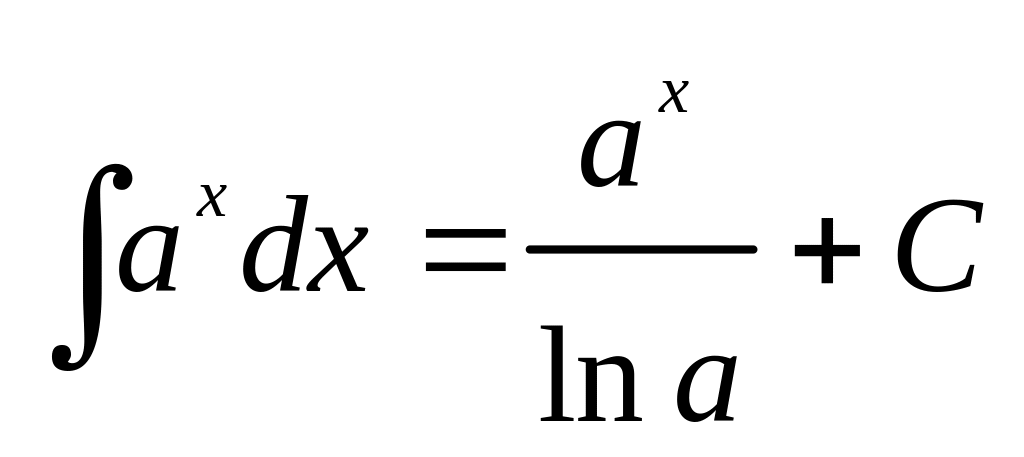 .
.
6)![]() .
.
7)![]() .
.
8)![]() .
.
9)![]() .
.
10)![]() .
.
11)![]() .
.
12)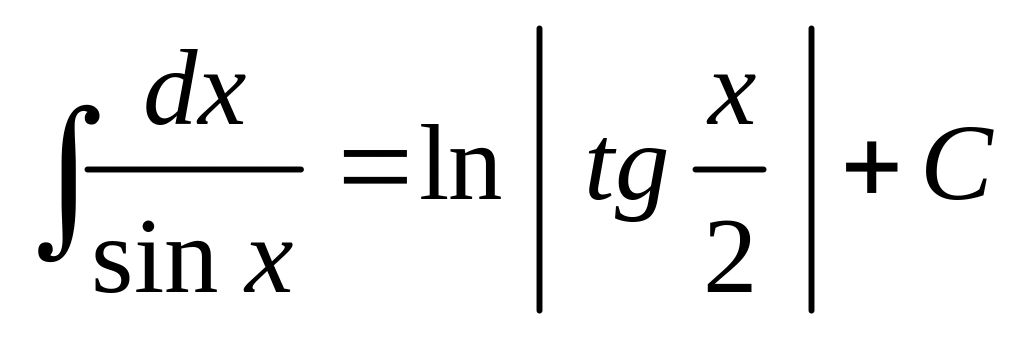 .
.
13)![]() .
.
14)![]() .
.
15)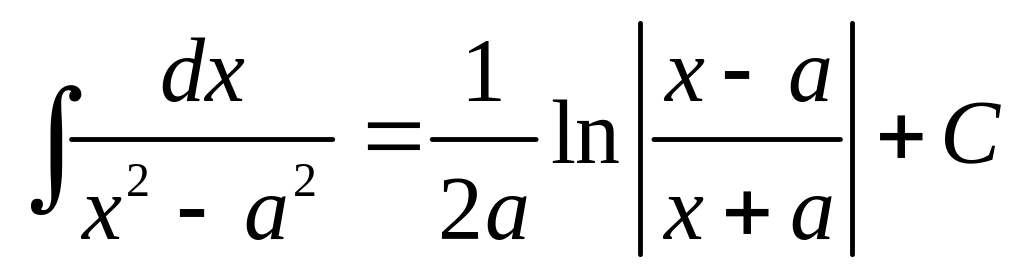 .
.
16)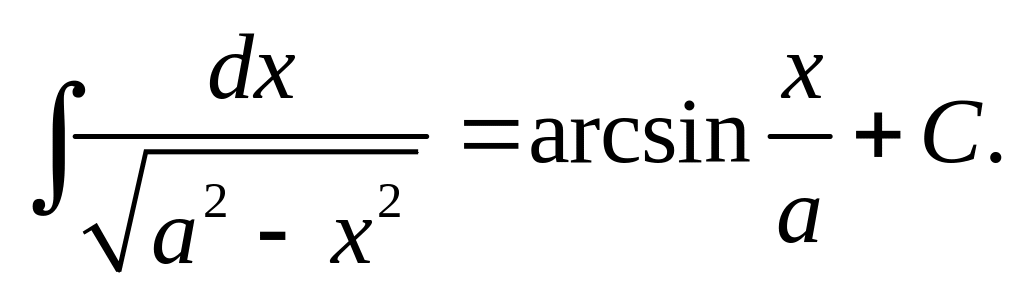
17)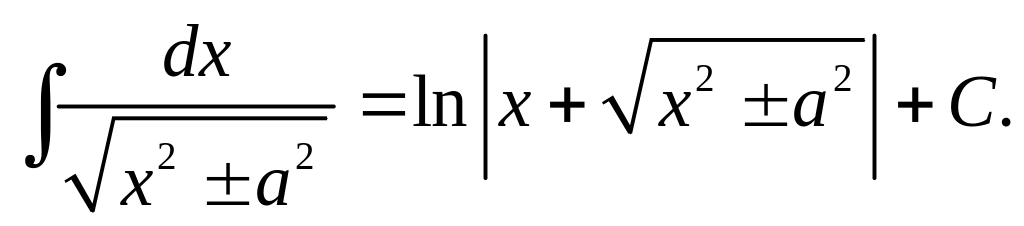
ПРИМЕР
1. Вычислить
интеграл
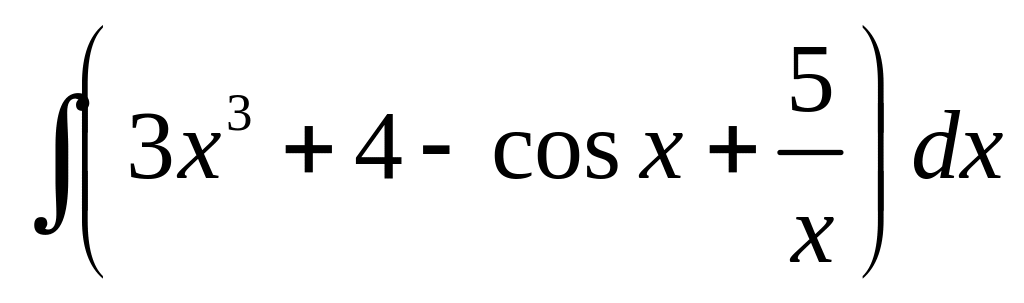 .
.
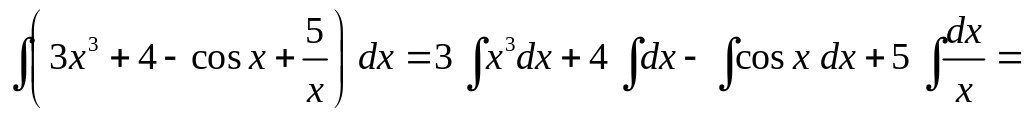
![]()
Здесь мы использовали свойства 4 (постоянный множитель можно выносить за знак интеграла) и 5 (интеграл от суммы двух функций равен сумме интегралов от этих функций), а также формулы 1, 2, 3, 7.
ПРИМЕР
2. Вычислить
интеграл
![]() .
.
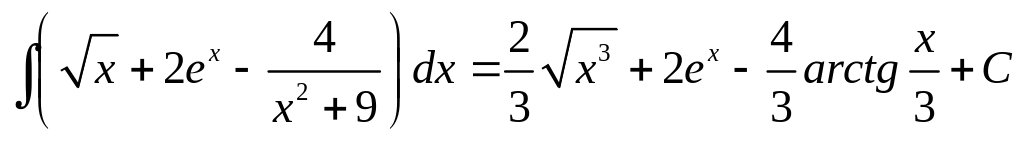 .
.
Для вычисления
интеграла от первого слагаемого
использовалась формула 2 и то, что
![]() :
:
 .
.
При вычислении интеграла от последнего слагаемого была использована формула 14 при а = 3.
Внесение под знак дифференциала
Одним из основных методов интегрирования является внесение функции под знак дифференциала. При его применении используется свойство 6.
ПРИМЕР
3. Вычислить
интеграл
![]() .
.
Под интегралом
стоит функция от (x2
+ 9) и x
в первой
степени. Так как
![]() ,
умножим и разделим выражение под
интегралом на 2 и заменим 2xdx
на d(x2
+ 9). Получим
,
умножим и разделим выражение под
интегралом на 2 и заменим 2xdx
на d(x2
+ 9). Получим
![]()
![]()
Если обозначить
![]() ,
то можно заметить, что получился табличный
интеграл (формула 2). Вычислим его и
вернёмся к переменной x.
,
то можно заметить, что получился табличный
интеграл (формула 2). Вычислим его и
вернёмся к переменной x.
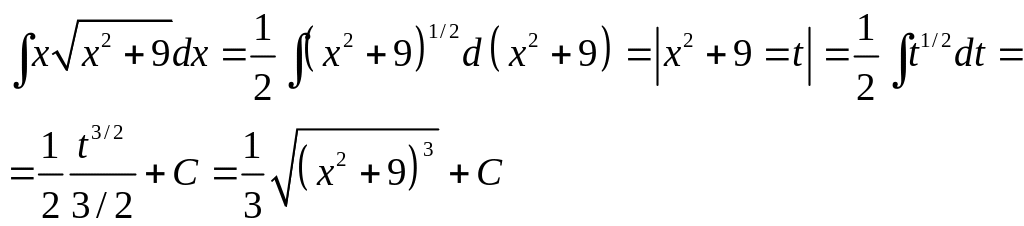
ПРИМЕР
4. Вычислить
интеграл
![]() .
.
![]()
![]()
![]()
ПРИМЕР
5. Вычислить
интеграл
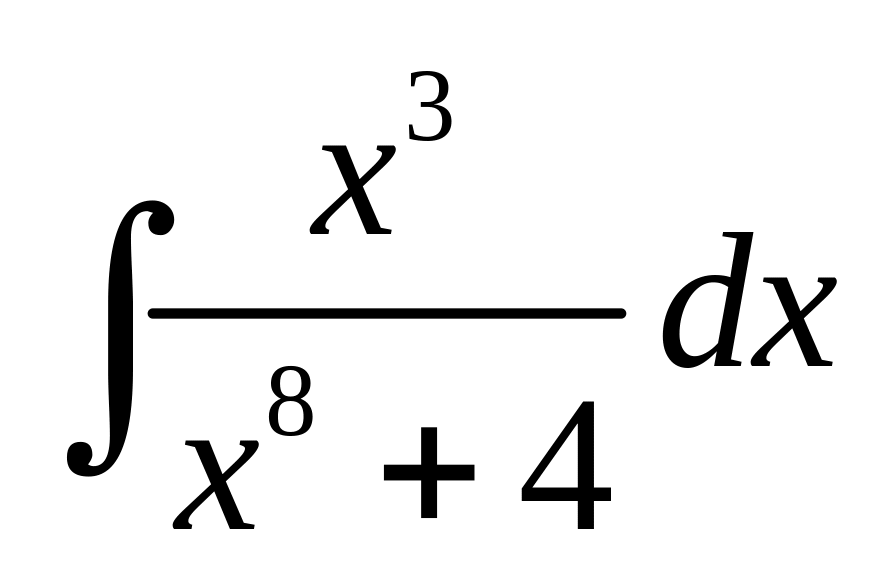 .
.
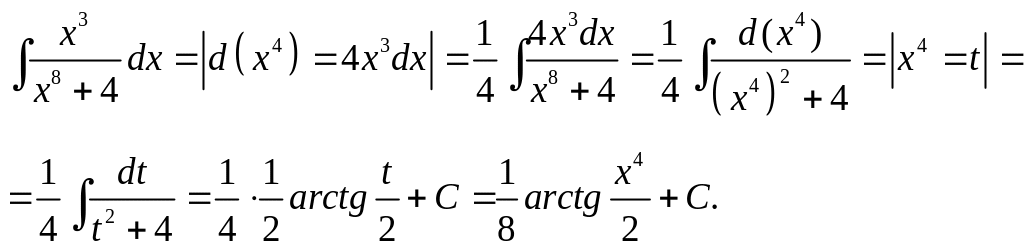
ПРИМЕР
6. Вычислить
интеграл
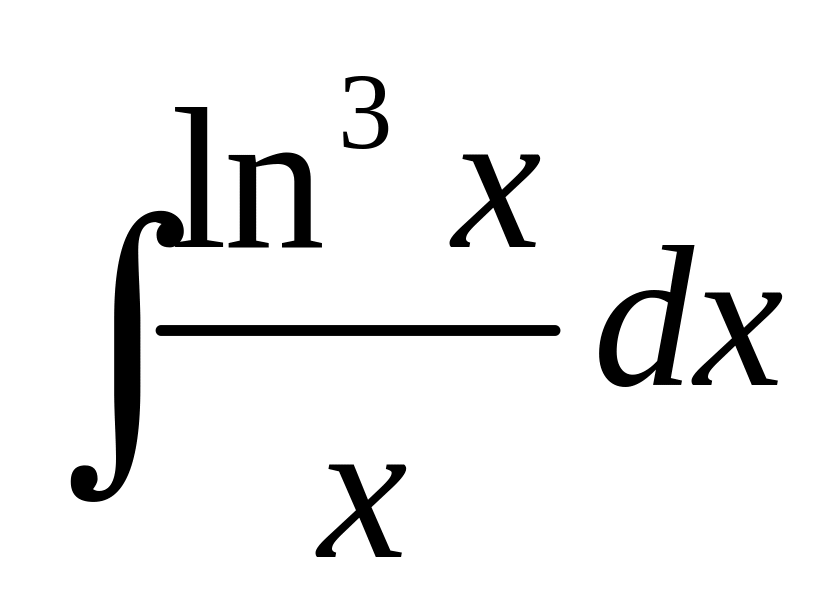 .
.
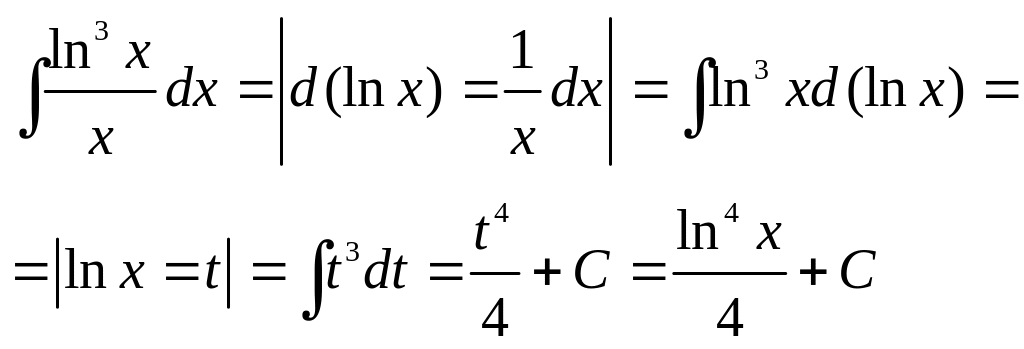
ПРИМЕР
7. Вычислить
интеграл
![]() .
.
![]()
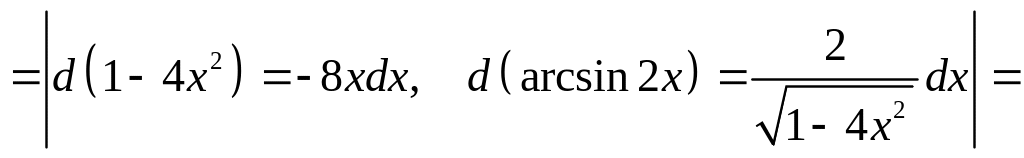

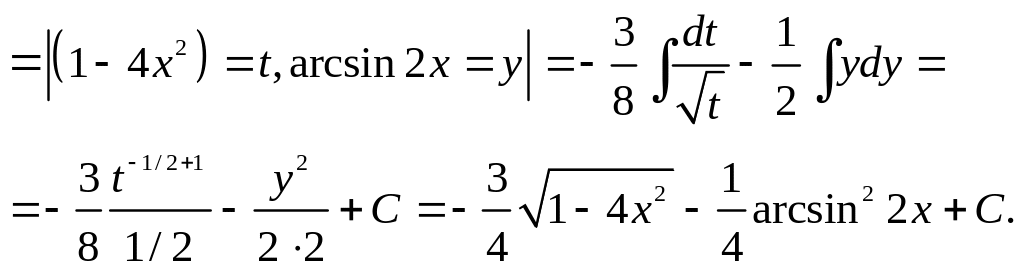
ПРИМЕР
8. Вычислить
интеграл
![]() .
.