Необходимый признак сходимости

Если ряд сходится, то .

Для решения примеров этот признак удобнее применять в следующем виде:

Е сли , то ряд расходится.

Заметим, что если , то ряд может быть как сходящимся, так и расходящимся и для его исследования нужно применять другие признаки.

ПРИМЕР 26. Исследовать на сходимость ряд .

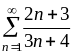0

0

следовательно, ряд расходится.

Рассмотрим некоторые достаточные признаки сходимости для положительных рядов.

Признак даламбера

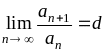Пусть дан ряд с положительными членами (a_n>0 для всех ) и . Тогда, если d > 1, то ряд расходится,

если d < 1, то ряд сходится,

если d = 1, то ряд может, как сходится, так и расходится.

Замечание 1. Признак Даламбера обычно применяется, если а_n содержит факториалы и (или) показательную функцию.

Замечание 2. Чтобы получить а_n+1, нужно в выражение для а_n вставить (n+1) вместо n.

ПРИМЕР 27. Исследовать на сходимость ряд .

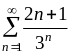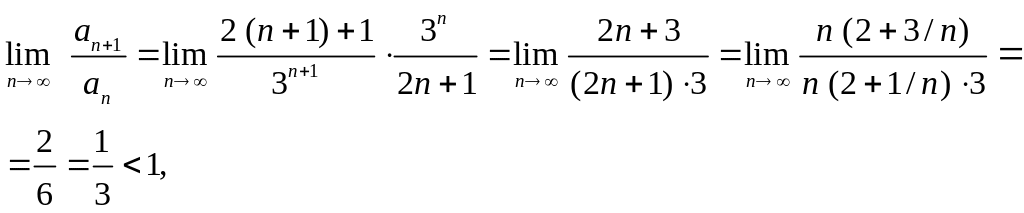
следовательно, ряд сходится.

ПРИМЕР 28 .Исследовать на сходимость ряд

,

т.е. ряд расходится.

ПРИМЕР 29. Исследовать на сходимость .

,

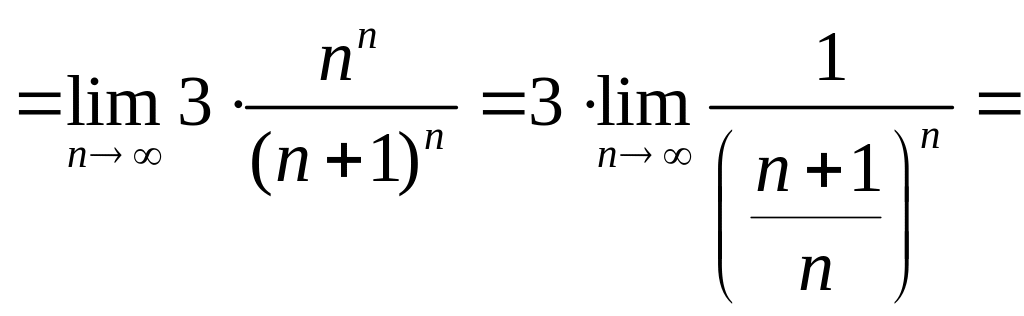
т. е. ряд расходится.

Напомним, что – второй замечательный предел.

Радикальный признак коши

Пусть дан ряд с положительными членами (a_n > 0 для всех n N) и Тогда,

если k > 1, то ряд расходится,

если k < 1, то ряд сходится,

если k = 1, то этот признак не работает.

Замечание. Обычно этот признак применяется, если а_n имеет вид или и т.д. При этом показатель корня в признаке Коши всегда n , независимо от показателя степени в a_n.

ПРИМЕР 30. Исследовать на сходимость ряд .

Напомним, что при извлечении корня показатели делятся, т.е.

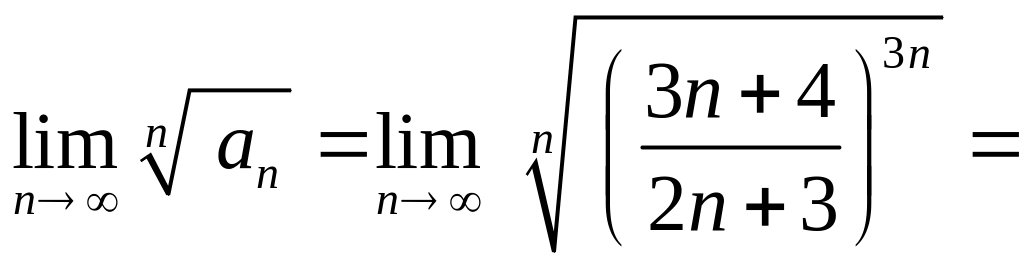
следовательно, ряд расходится.

ПРИМЕР 31. Исследовать на сходимость ряд .

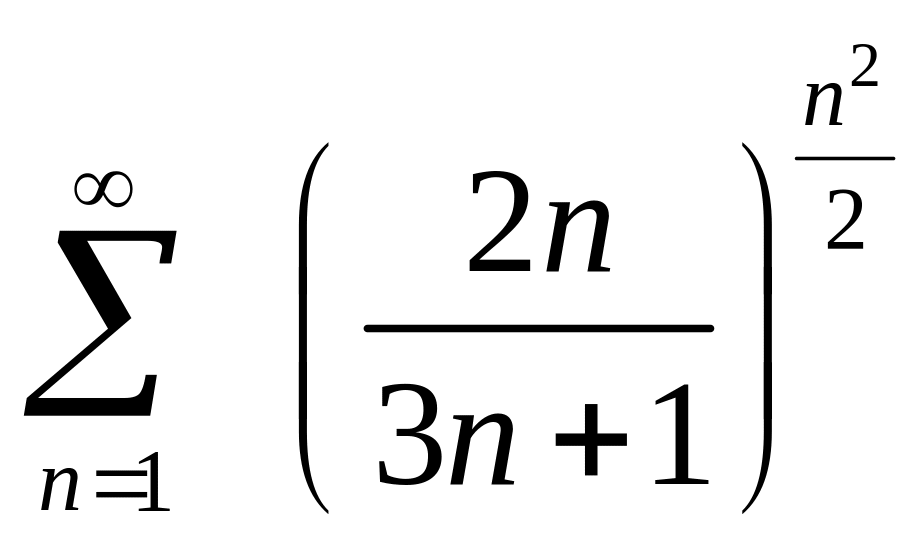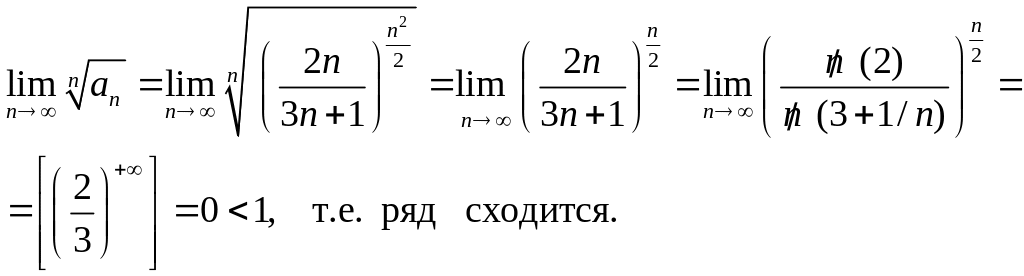
Здесь использовано свойство показательной функции y(x) = а^х .

Интегральный признак коши

Пусть члены ряда положительны и не возрастают, а функция f(x) на [k, ]: 1) непрерывна;

2) положительна;

3) не возрастает;

4) f (n) = a_n.

Тогда ряд и несобственный интеграл являются равносходящимися, то есть сходятся или расходятся одновременно.

ПРИМЕР 32. Исследовать на сходимость ряд .

Так как знаменатель дроби n ln n возрастает при , то убывает. Кроме того, при n > 1 n ln n > 0.

Заменяя n на x, получим функцию , удовлетворяющую всем условиям теоремы. Пределы интегрирования соответствуют пределам изменения n для ряда. Итак, .

Напомним, что .

Если предел существует и конечен, то интеграл (а, следовательно, и ряд) сходится. Если же предел равен , то интеграл (а, следовательно, и ряд) расходится.

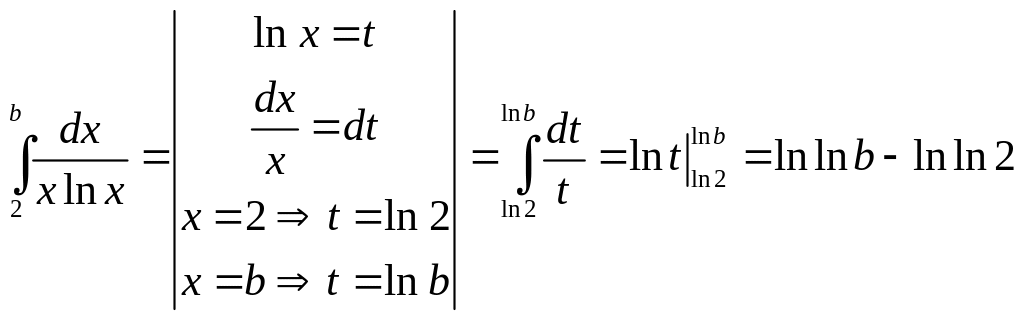
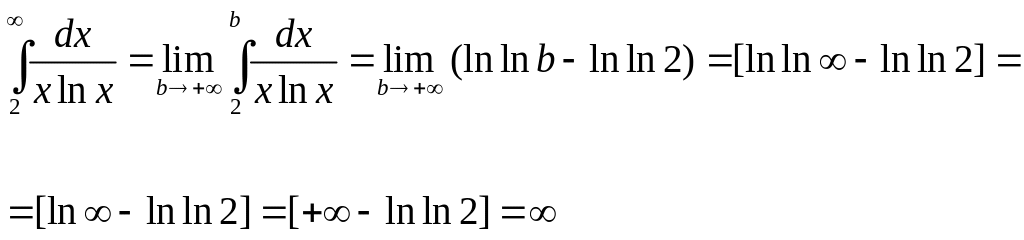
То есть и интеграл, и ряд расходятся.

ПРИМЕР 33. Исследовать на сходимость ряд .

=

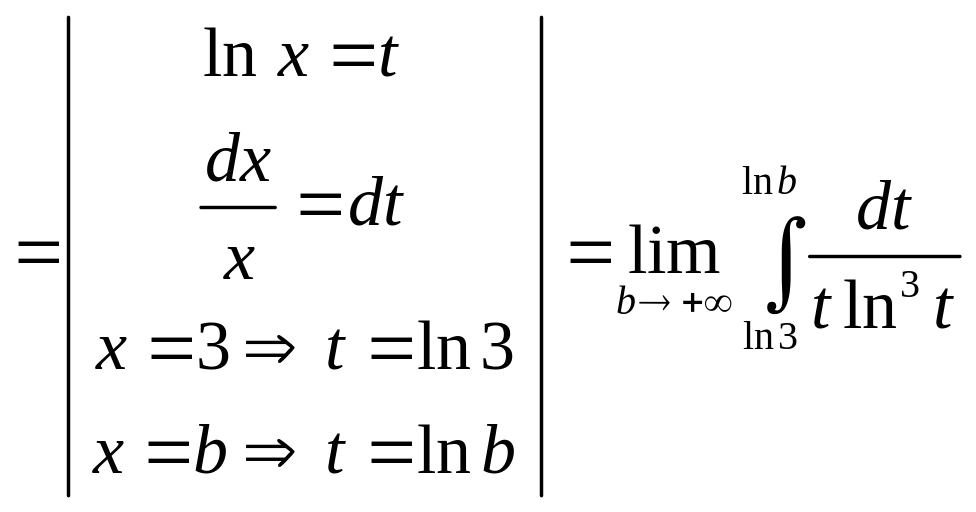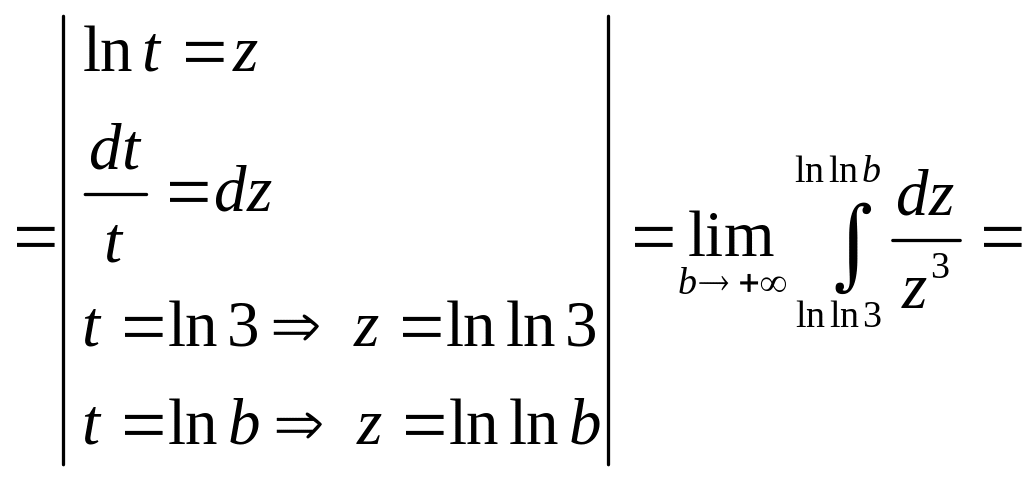
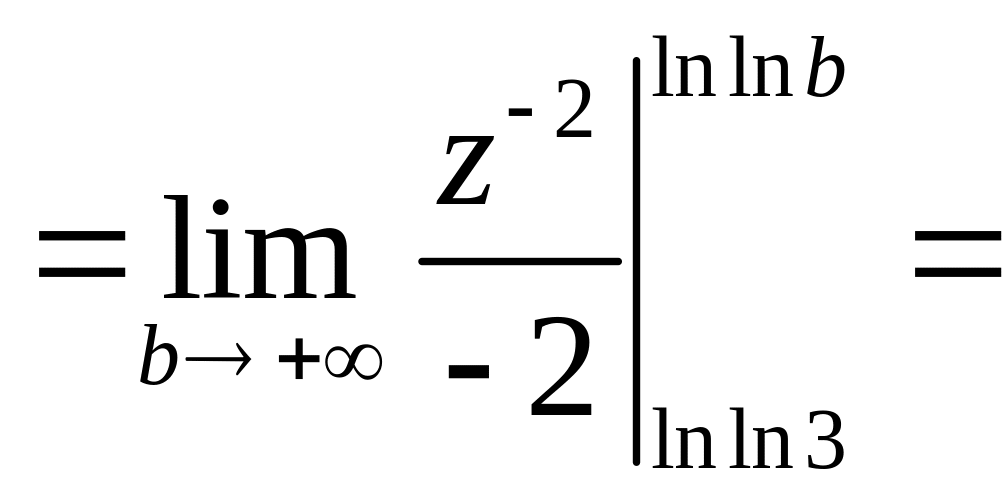
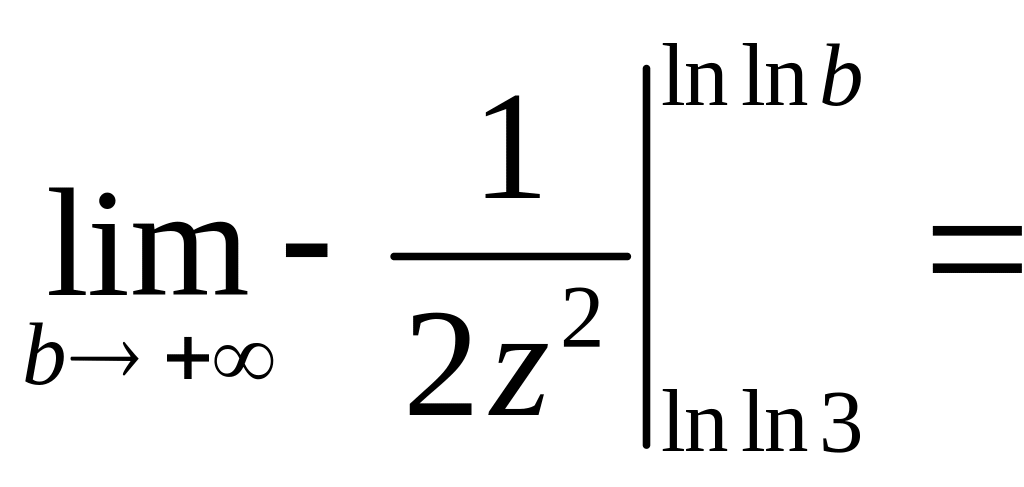
Интеграл и ряд сходятся.

Признак сравнения

Пусть и – ряды с положительными членами. Если, начиная с некоторого номера выполняется неравенство , то из сходимости ряда следует сходимость ряда , а из расходимости ряда следует расходимость ряда .

З амечание 1. Обычно исследуемый ряд сравнивают с «эталонным» рядом :

сходится при ,

расходится при .

Замечание 2. Признак сравнения приходится применять, если общий член ряда содержит и при этом применение интегрального признака Коши приводит к трудно вычисляемому интегралу.

При этом используются следующие неравенства:

для всех и более «тонкое»:

(для и , то есть x( ), начиная с которого , зависит от ).

ПРИМЕР 34. Исследовать на сходимость ряд .

Воспользуемся неравенством . При переходе к обратным величинам знаки неравенства меняются, то есть . Ряд расходится, так как (необходимый признак), то есть его сумма равна , но исследуемый ряд состоит из меньших членов, следовательно, его сумма может быть как числом, так и .

Рассмотрим ряд из меньших членов = – это «эталонный» ряд с , то есть расходящийся ряд.

Так как и ряд расходится, то по признаку сравнения ряд так же расходится.

ПРИМЕР 35. Исследовать на сходимость ряд .

Воспользуемся неравенством , . Все части неравенства положительны, поэтому их можно возвести в квадрат, и знаки неравенства не изменятся.

Разделим все члены неравенства на . Так как > 0, то знаки неравенства не меняются.

.

Ряд с меньшими членами сходится . Из этого сделать вывод о сходимости или расходимости ряда с большими членами нельзя.

Ряд с большими членами

расходится. Это так же не позволяет сделать определенный вывод о

сходимости исследуемого ряда.

Воспользуемся неравенством

, где

.

При

Ряд сходится при , то есть при , . Числа , удовлетворяющие условию существуют, например, . Итак,

, а этот ряд сходится. Следовательно, и ряд с меньшими членами сходится.