1. Основные понятия теории вероятностей. Случайные события. Вероятность.

Достоверное событие.

Событие называется достоверным, если оно обязательно произойдет при осуществлении определенной совокупности условий.

Обозначение: И (истина).

Пример: игральный кубик подбрасывается вверх, выпадет число от 1 до 6 (это достоверное событие).

Невозможное событие. Событие, которое никогда не произойдет при определенной совокупности условий.

Обозначение: V

Случайное событие. Может произойти или не произойти при выполнении определенной совокупности условий.

Обозначение: A, B, C{\ldots}

События A и B будем называть несовместными, если появление события A исключает возможность появление события B. Иначе события будем называть совместными.

События называются равновозможными, если в результате испытаний ни одно из них не является более возможным, чем другое.

Полная группа событий.

События будут образовывать полную группу, если в результате испытаний появится хотя бы одно из них.

Пример: Ai - i-е число на вершине грани кубика.

Противоположные события - события, которые являются 2-мя возможными исходами одного испытания.

Обозначение: A,  A

Примеры:

1. A - орел, A - решка; A

2. A - попадание в мишень, A - промах.

Задача 1. Из колоды в 36 карт извлекают 4 карты. Событие A - все карты одной масти. Назовите событие, противоположное для A.

Ответ. A - хотя бы 2 карты разной масти

Вероятностью случайного события p(A) называется отношение числа благоприятствующих данному событию исходов к общему числу всех равновозможных несовместных исходов, образующих полную группу.

Свойства вероятности: 

1. И -- достоверное событие, p(И)=1(вероятность достоверного события = 1)

2. V -- невозможное событие, p(V)=0 (вероятность невозможного события = 0)

3. 0≤p(A)≤1  

Задача 2. В коробке имеется 7 карандашей. Из них 2 красных. Из коробки наугад извлекают 1 карандаш. Найти вероятность того, что этот карандаш будет красным.

Решение. Число благоприятствующих данному событию исходов равно 2 (т.к. в коробке 2 красных карандаша). Общее число исходов равно 7 (количество карандашей в коробке). Тогда вероятность того, что этот карандаш будет красным p(A)=72.

Задача 3. Бросаются 2 игральные кости. Найти вероятность того, что сумма очков будет равна 8.

Решение. Количество благоприятных исходов будет равно 6 (6 и 2, 5 и 3, 4 и 4, 3 и 5, 2 и 6). Всего возможных исходов 36. Следовательно, p(A)=536

Задача 4. Абонент, набирая номер телефона забыл одну из цифр. Найти вероятность того, что будет набрана правильная цифра.

Ответ: p(A)=110

2. Пространство элементарных событий — множество Ω всех взаимно или попарно исключающих друг друга исходов случайного эксперимента, которые вместе образуют полную группу событий.

Элемент этого множества называется элементарным событием или исходом. Пространство элементарных событий называется дискретным, если число его элементов конечно или счётно. Любое пространство элементарных событий не являющееся дискретным, называется недискретным, и при этом, если наблюдаемыми результатами (нельзя произносить случайными событиями) являются точки того или иного числового арифметического или координатного пространства, то пространство называется непрерывным (континуум). Пространство элементарных событий Ω вместе с алгеброй событий и вероятностью образует тройку , которая называется вероятностным пространством.

Операции над случайными событиями

При вычислениях вероятности появления того или иного события часто приходится  рассматривать его как совокупность других событий. Таким образом,  возникает необходимость производить преобразования,  для чего устанавливают правила таких преобразований.

1. Если событие А происходит при появлении события В, то говорят, что В включает в себя А и записывают:  .

2. Если , то А=В.

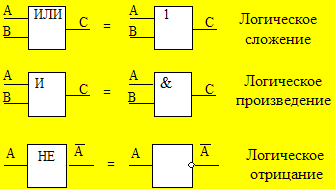
3. Событие  называется противоположным событию А,  если оно состоит в том, что событие А не происходит.  4. Произведением событий А и В называют событие С=АxВ , которое означает, что А и В происходят одновременно 5. Суммой 2-х  событий А и В  называют событие С=А+В, которое означает, что происходит либо событие А, либо событие В, либо А и В одновременно. А+В принадлежит АxВ; В вычислительной технике существуют  элементы , которые выполняют указанные операции  над сигналами.

 

           

3. Классическое определение вероятности. при большом числе n испытаний частота P*(A)=m/n появления события A обладает устойчивостью и дает приближенное значение вероятности события A, т.е. .    Это обстоятельство позволяет находить приближенно вероятность события опытным путем. Практически такой способ нахождения вероятности события не всегда удобен. В ряде случаев вероятность события удается определить до опыта с помощью понятия равновероятности событий (или равновозможности).

  Два события называются равновероятными (или равновозможными), если нет никаких объективных причин считать, что одно из них может наступить чаще, чем другое.    Так, например, появления герба или надписи при бросании монеты представляют собой равновероятные события.    Рассмотрим другой пример. Пусть бросают игральную кость. В силу симметрии кубика можно считать, что появление любой из цифр 1, 2, 3, 4, 5 или 6 одинаково возможно (равновероятно).    События E1,E2, ..., EN в данном опыте образуют полную группу, если в результате опыта должно произойти хотя бы одно из них.    Так, в последнем примере полная группа событий состоит из шести событий — появлений цифр 1, 2, 3, 4, 5 и 6.    Очевидно, любое событие A и противоположное ему событие образуют полную группу.    Событие B называется благоприятствующим событию A, если наступление события B влечет за собой наступление события A.    Так, если A — появление четного числа очков при бросании игральной кости, то появление цифры 4 представляет собой событие, благоприятствующее событию A.    Пусть события E1,E2, ..., EN в данном опыте образуют полную группу равновероятных и попарно несовместных событий. Будем называть их исходами испытания. Предположим, что событию A благоприятствуют M исходов испытания. Тогда вероятностью события A в данном опыте называют отношение M/N. Итак, мы приходим к следующему определению.    Вероятностью P(A) события в данном опыте называется отношение числа M исходов опыта, благоприятствующих событию A, к общему числу N возможных исходов опыта, образующих полную группу равновероятных попарно несовместных событий:

   Это определение вероятности часто называют классическим. Можно показать, что классическое определение удовлетворяет аксиомам вероятности.    Пример 1. На завод привезли партию из 1000 подшипников. Случайно в эту партию попало 30 подшипников, не удовлетворяющих стандарту. Определить вероятность P(A) того, что взятый наудачу подшипник окажется стандартным. (Решение) Число стандартных подшипников равно 1000—30=970. Будем считать, что каждый подшипник имеет одинаковую вероятность быть выбранным. Тогда полная группа событий состоит из N=1000 равновероятных исходов, из которых событию A благоприятствуют М=970 исходов. Поэтому P(A)=M/N=970/1000=0.97    Пример 2. В урне 10 шаров: 3 белых и 7 черных. Из урны вынимают сразу два шара. Какова вероятность р того, что оба шара окажутся белыми? (Решение)   Решение: Число N всех равновероятных исходов испытания равно числу способов, которыми можно из 10 шаров вынуть два, т. е. числу сочетаний из 10 элементов по 2:

   Число благоприятствующих исходов:    Следовательно, искомая вероятность

   Пример 3. В урне 2 зеленых, 7 красных, 5 коричневых и 10 белых шаров. Какова вероятность появления цветного шара? (Решение)

 Решение: Находим соответственно вероятности появления зеленого, красного и коричневого шаров: Р(зел.)=2/24; Р(кр.)=7/24; Р(кор.)=5/24. Так как рассматриваемые события, очевидно, несовместны, то, применяя аксиому сложения, найдем вероятность появления цветного шара:

4. Комбинаторика - раздел математики, рассматривающий вопросы создания совокупностей (комбинаций, соединений) из заданного множества объектов (элементов), подчиненных соответствующим  правилам или условиям.

Комбинаторика решает задачи, связанные с нахождением числа   комбинаций определенного типа, которые  можно составить из элементов заданного множества (группы) элементов (объектов)

Комбинаторика изучает количества комбинаций, подчиненных определенным условиям, которые можно со­ставить из элементов, безразлично какой природы, задан­ного конечного множества. При непосредственном вычис­лении вероятностей часто используют формулы комбина­торики. Приведем наиболее употребительные из них.

С комбинаторными задачами приходится встречаться в самых разных областях знаний и деятельности человека. Это: информатика, математика, физика, биология. лингвистика и др.: Много комбинаторных задач используется при организации и приведения досуга: фокусы, шарады,  лотереи и др. Игра в шахматы, шашки, нарды, карты и др. связаны с комбинаторикой.

Люди с глубокой древности интересовались комбинаторными задачами. Так, в пирамиде Тутанхамона, построенной  более, чем 35 веков  назад обнаружена доска с тремя горизонтальными и десятью вертикалями линиями для игры в “сенет”, прототип игры в шахматы и шашки. Правила в эту игру, к сожалению, обнаружить до сих пор не удалось.

Комбинаторика в таковых ситуациях усматривается в продумывании сразу нескольких комбинаций ходов (вариантов), которые могут привести к решению задачи наиболее кратким и быстрым путем.