
- •Операции над случайными событиями
- •1 Правило суммы и произведения.
- •5. Теоремы сложения и умножения вероятностей
- •8. Формула полной вероятности и формула Байеса
- •10. Теоремы Муавра-Лапласа
- •13. Дискретная случайная величина и закон ее распределения
- •15. Вероятность и числовые ряды
- •19. 3.2 Геометрическое рапределение
- •Пример 3.2
8. Формула полной вероятности и формула Байеса
Если
событие
![]() может
наступить только при появлении одного
из несовместных событий (гипотез)
может
наступить только при появлении одного
из несовместных событий (гипотез)
![]() ,
то вероятность события
вычисляется
по формуле полной
вероятности:
,
то вероятность события
вычисляется
по формуле полной
вероятности:
![]() ,
где
,
где
![]() -
вероятность гипотезы
-
вероятность гипотезы
![]() ,
,
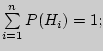
![]() -
условная вероятность события
при
выполнении гипотезы
(
-
условная вероятность события
при
выполнении гипотезы
(
![]() .
.
Проиллюстрируем формулу полной вероятности на графе с выделенной вершиной:

Рис. 17
Полная вероятность события равна весу всего вероятностного графа с гипотезами.
С
формулой полной вероятности тесно
связана формула Байеса. Если до опыта
вероятности гипотез были
![]() ,
,
![]() ,
...,
,
...,
![]() ,
а в результате опыта появилось событие
,
то с учетом этого события "новые",
т.е. условные вероятности гипотез
вычисляются по формуле Байеса
,
а в результате опыта появилось событие
,
то с учетом этого события "новые",
т.е. условные вероятности гипотез
вычисляются по формуле Байеса

Формула
Байеса дает возможность "пересмотреть"
вероятность гипотез с учетом наблюдавшегося
результата опыта. Условная вероятность
![]() может
находиться как отношение веса ветви,
проходящей через вершину, соответствующую
гипотезе
может
находиться как отношение веса ветви,
проходящей через вершину, соответствующую
гипотезе
![]() ,
к весу всего вероятностного графа.
,
к весу всего вероятностного графа.
Пример 31. На заводе, изготовляющем болты, первая машина производит 25%, вторая - 35%, третья - 40% всех изделий. В их продукции брак составляет соответственно 5, 4 и 2%.
а) Какова вероятность того, что случайно выбранный болт дефектный?
б) Случайно выбранный из продукции болт оказался дефектным. Какова вероятность того, что он был произведен первой, второй, третьей машиной?
Решение. Пусть событие = {выбрать дефектный болт}.
Выдвигаем три гипотезы:
![]() ={болт
изготовлен первой машиной},
=0,25,
={болт
изготовлен первой машиной},
=0,25,
![]() =0,05;
=0,05;
![]() ={болт
изготовлен второй машиной},
=0,35,
={болт
изготовлен второй машиной},
=0,35,
![]() =0,04;
=0,04;
![]() ={болт
изготовлен третьей машиной},
={болт
изготовлен третьей машиной},
![]() =0,4,
=0,4,
![]() =0,02.
=0,02.

Рис. 18
а)
![]()
б)
![]()
![]()
![]()
Пример 32. Студент подготовил к экзамену 20 билетов из 25. В каком случае шансы взять известный билет больше - когда студент пришел на экзамен первым или вторым?
Решение.
![]() Найдем
вероятность
Найдем
вероятность
![]() взять
известный билет, придя на экзамен вторым,
учитывая, что первый может взять как
известный, так и неизвестный второму
билет.
взять
известный билет, придя на экзамен вторым,
учитывая, что первый может взять как
известный, так и неизвестный второму
билет.

Рис. 19
![]()
Пример 33. Наудачу выбираем колоду, а из нее карту. В каком случае вероятность достать туз больше: если выбирать карту из двух колод, содержащих по 32 и 52 карты, или выбирать карту из трех колод в 36 карт и одной в 52?
Решение.
Пусть событие
![]() =
{ достать туз}.
=
{ достать туз}.

Рис. 20
![]()
![]() ,
следовательно, в первом случае вероятность
достать туз меньше, чем во втором.
,
следовательно, в первом случае вероятность
достать туз меньше, чем во втором.
Пример 34. В каждой из трех урн содержится по одному белому и одному черному шару. Из первой урны во вторую переложили один шар, из второй пополненной урны в третью тоже переложили один шар, а затем из третьей урны наудачу извлекли один шар. Какова вероятность извлечь белый шар из третьей пополненной урны?
Решение.

Рис. 21
![]()
Какие гипотезы использовались в решении этой задачи?
Пример 35. Предположим, что 5 мужчин из 100 и 25 женщин из 10000 являются дальтониками. Наугад выбранное лицо страдает дальтонизмом. Какова вероятность, что это мужчина?
Решение.

Рис. 22

9. Схема Бернулли состоит в следующем: производится последовательность испытаний, в каждом из которых вероятность наступления определенного события А одна и та же и равна р. Испытания предполагаются независимыми (т.е. считается, что вероятность появления события А в каждом из испытаний не зависит от того, появилось или не появилось это событие в других испытаниях). Наступление события А обычно называют успехом, а ненаступление - неудачей. Обозначим вероятность неудачи q=1-P(A)=(1-p). Вероятность того, что в n независимых испытаниях успех наступит ровно m раз, выражается формулой Бернулли:
![]()
Вероятность Рn(m) при данном n сначала увеличивается при увеличении m от 0 до некоторого значения m0, а затем уменьшается при изменении m от m0 до n. Поэтому m0, называют наивероятнейшим числом наступлений успеха в опытах. Это число m0, заключено между числами np-q и np+p (или, что то же самое, между числами n(p+1)-1 и n(p+1)) .Если число np-q - целое число, то наивероятнейших чисел два: np-q и np+p. Важное замечание. Если np-q< 0, то наивероятнейшее число выигрышей равно нулю.
