
- •Раздел 6
- •Повторение
- •1. Неопределенный интеграл
- •1.1. Первообразная функции. Неопределенный интеграл
- •1.2. Свойства неопределенного интеграла
- •1.3. Таблица основных неопределенных интегралов
- •2. Методы интегрирования
- •2.1. Метод непосредственного интегрирования
- •2.2. Метод интегрирования подстановкой (заменой переменной)
- •2.3. Метод интегрирования по частям
- •3. Интегрирование рациональных,
- •3.1. Понятия о рациональной функции
- •3.1.1. Многочлен
- •3.1.2. Дробно-рациональная функция
- •3.2. Интегрирование рациональных дробей
- •3.3. Интегрирование тригонометрических функций
- •3.3.1. Интегралы вида
- •3.3.2. Интегралы вида
- •3.4.2. Дробно-линейная подстановка
- •3.4.3. Тригонометрическая подстановка
- •3.4.4. Интегрирование дифференциального бинома
- •3.5. «Берущиеся» и «неберущиеся» интегралы
- •I. О технике интегрирования
- •II. Использование таблиц интегрирования
- •III. Об интегрировании в элементарных функциях
- •4. Определенный интеграл
- •4.1. Понятие определенного интеграла
- •Задача о площади криволинейной трапеции
- •Задача о работе переменой силы
- •4.2. Основные свойства определенного интеграла
- •4.3. Формула НьютонаЛейбница
- •4.4. Вычисление определенного интеграла
- •5. Несобственные интегралы
- •5.1. Интеграл с бесконечным промежутком интегрирования (несобственный интеграл первого рода)
- •5.2. Интеграл от разрывной функции (несобственный интеграл второго рода)
Раздел 6
ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ
ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ
Повторение
В I-ом семестре был изучен раздел «Дифференциальное исчисление». Были введены понятия «производная функции в точке» и «дифференциал функции». Напомним эти понятия.
Определение. Производной функции
![]() в точке
в точке
![]() называется предел отношения приращения
функции к приращению аргумента, когда
приращение аргумента стремится к нулю,
т.е.
называется предел отношения приращения
функции к приращению аргумента, когда
приращение аргумента стремится к нулю,
т.е.
 ,
,
или
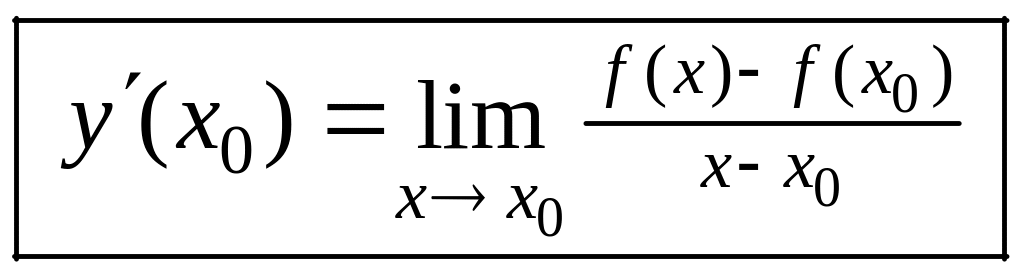 .
.
Определение. Дифференциалом
функции
в точке x
называется главная часть ее приращения,
равная произведению производной функции
на приращение аргумента, и обозначается
![]() (или
(или
![]() ):
):
![]() .
.
Были введены правила дифференцирования.
Теорема. Если функции
![]() и
и
![]() дифференцируемы в точке x,
то функции
дифференцируемы в точке x,
то функции
![]() ,
,
![]() и
и
![]() дифференцируемы в этой точке, причем:
дифференцируемы в этой точке, причем:
1)
![]() ;
;
2)
![]() ,
в частности
,
в частности
![]() ,
где
,
где
![]() ;
;
3)
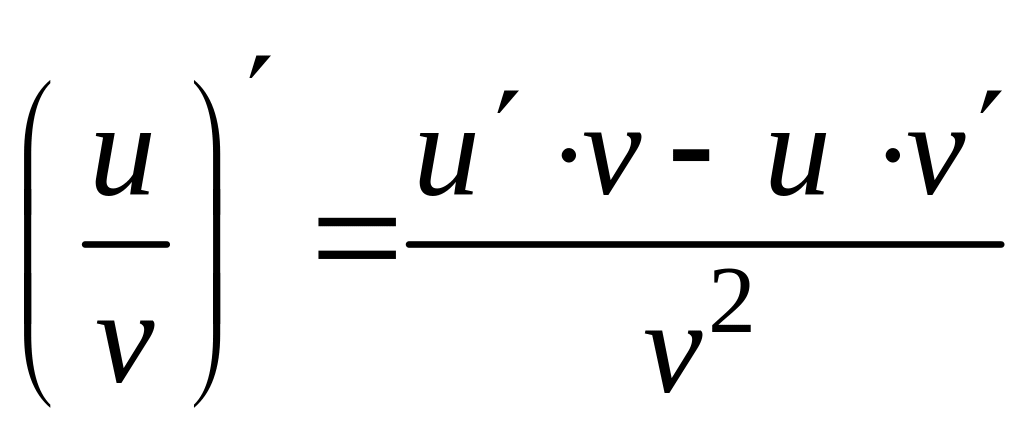 .
.
На основе определения производной функции в точке и теорем о производной сложной и обратной функций, а также правил дифференцирования была составлена таблица производных элементарных функций.
1.
![]() ;
7.
;
7.
![]() ;
13.
;
13.
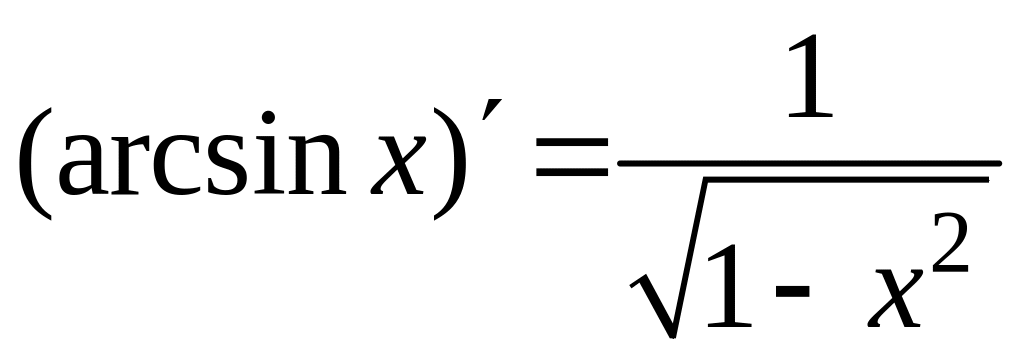 ;
;
2.
![]() ;
8.
;
8.
![]() ;
14.
;
14.
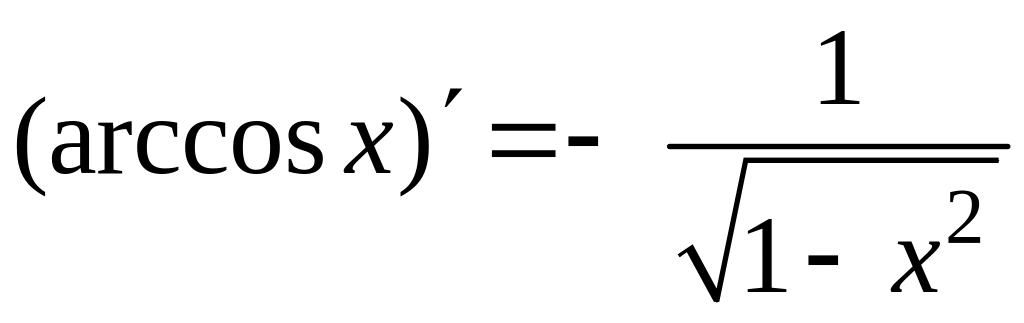 ;
;
3.
![]() ;
9.
;
9.
![]() ;
15.
;
15.
![]() ;
;
4.
 ;
10.
;
10.
![]() ;
16.
;
16.
![]() .
.
5.
![]() ;
11.
;
11.
![]() ;
17.
;
17.
![]() ;
;
6.
![]() ;
12.
;
12.
![]() ;
18.
;
18.
![]() ;
;
19.
![]() ;
;
20.
![]() .
.
Пример 1. Найти производную следующей
функции:
![]() .
.
Решение.
![]() .
.
Пример 2. Найти дифференциал функции:
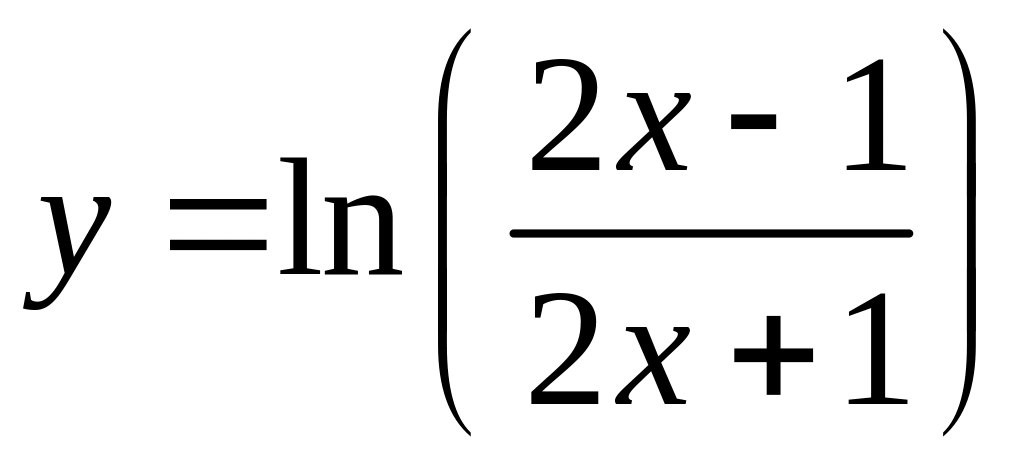 .
.
Решение. Находим производную функции:
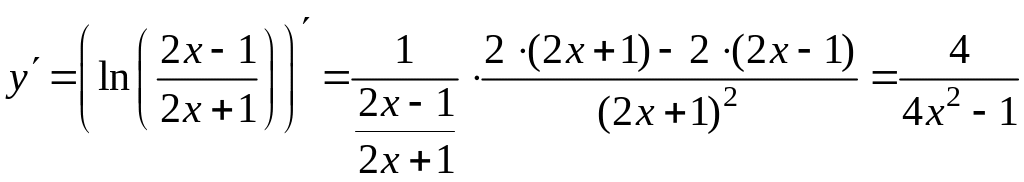 .
.
Далее находим дифференциал:
![]() .
.
Поставим обратную задачу.
Пример 3. Найти функцию
![]() ,
зная дифференциал этой функции:
,
зная дифференциал этой функции:
1)
![]() ;
;
2)
![]() .
.
Решение. Используя таблицу
производных, подносим функцию
![]() под знак дифференциала, и находим функцию
.
под знак дифференциала, и находим функцию
.
1)
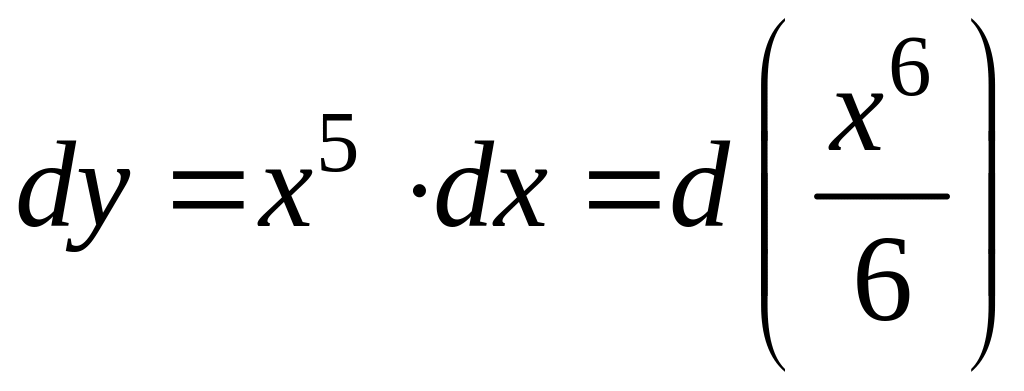 ,
,
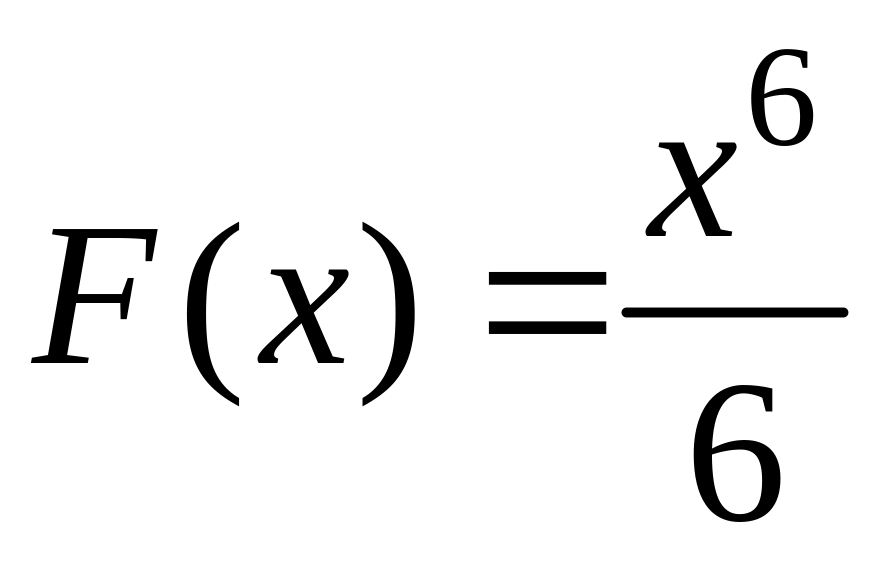 .
.
Проверка:
 .
.
2)
![]() ,
,
![]() .
.
Проверка:
![]() .
.
1. Неопределенный интеграл
1.1. Первообразная функции. Неопределенный интеграл
В дифференциальном исчислении решается
задача: по данной функции
найти ее производную (или дифференциал).
Теперь перейдем к изучению обратной
задачи, которая имеет очень большое
значение в анализе и его приложениях:
найти функцию
,
зная ее производную (или дифференциал),
т.е. выполняется условие
![]() .
Искомая функция
называется первообразной для функции
.
.
Искомая функция
называется первообразной для функции
.
Например, для функции
![]() мы нашли функцию
,
для которых выполнялось условие
.
Поэтому искомая функция
является первообразной для функции
.
мы нашли функцию
,
для которых выполнялось условие
.
Поэтому искомая функция
является первообразной для функции
.
Определение 1.1. Функция
называется первообразной для
функции
на интервале
![]() ,
если для любого
,
если для любого
![]() выполняется равенство
выполняется равенство
или
![]() .
.
Замечание. Понятие первообразной можно ввести и для других промежутков (отрезка, полуинтервала – конечного или бесконечного).
Например, для функции
![]() первообразной является функция
первообразной является функция
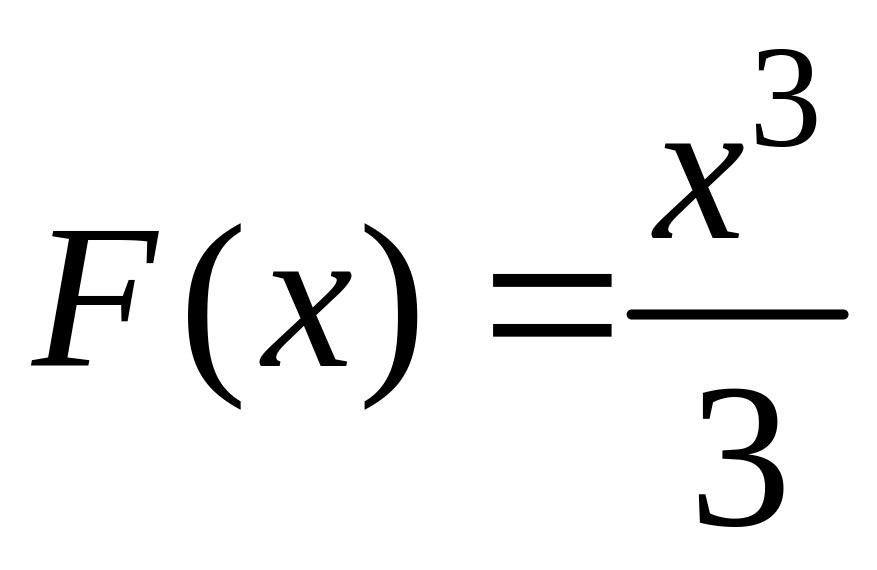 ,
так как
,
так как
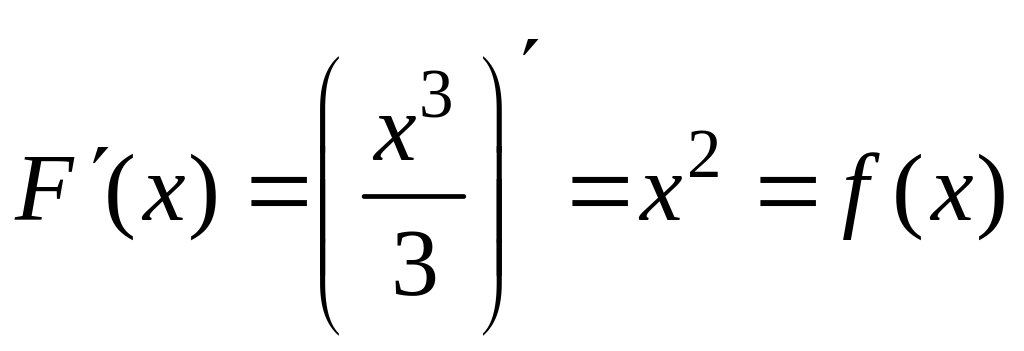 .
.
Но не только функция
является первообразной для функции
![]() .
Функции
.
Функции
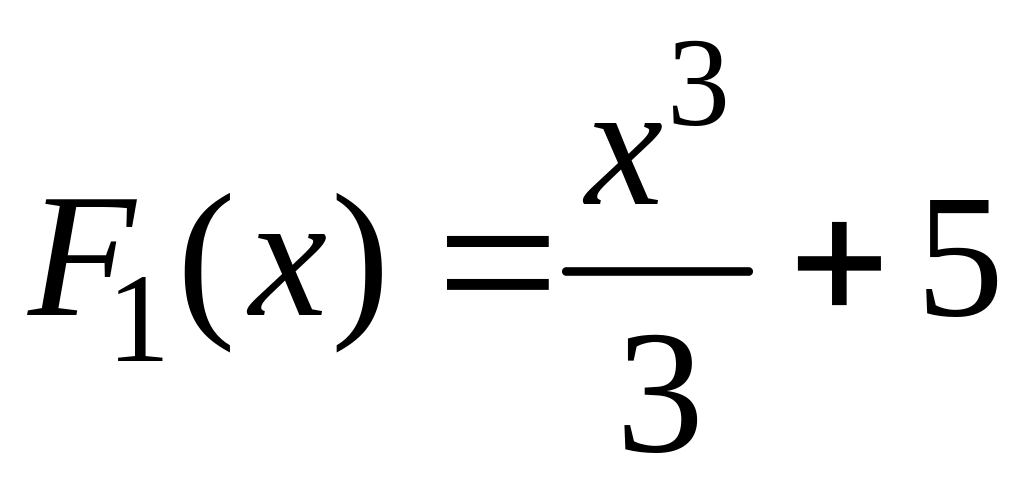 ,
,
 ,
,
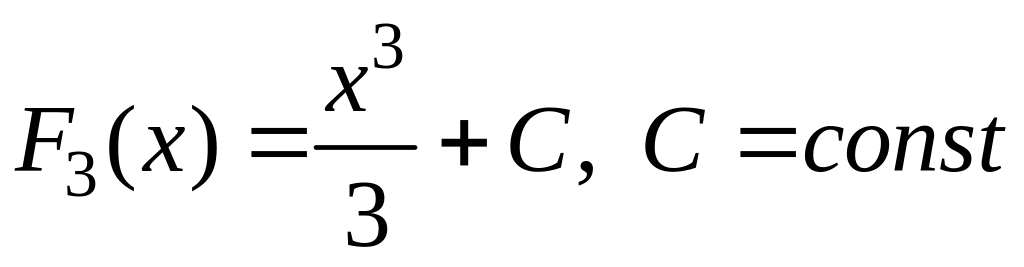 тоже являются первообразными для функции
.
Причем в функцию
тоже являются первообразными для функции
.
Причем в функцию
 вместо
вместо
![]() можно подставить любое действительное
число. Таким образом, напрашивается
следующий вывод: первообразных у данной
функции не одна, а бесчисленное множество,
так как постоянная величина
может принимать любое значение;
производных же у данной функции,
разумеется, только одна.
можно подставить любое действительное
число. Таким образом, напрашивается
следующий вывод: первообразных у данной
функции не одна, а бесчисленное множество,
так как постоянная величина
может принимать любое значение;
производных же у данной функции,
разумеется, только одна.
Сформулируем и докажем основную теорему о первообразной.
Теорема 1.1. Всякая непрерывная на интервале функция имеет бесчисленное множество первообразных, причем любые две из них отличаются друг от друга только постоянным слагаемым.
Доказательство. Наиболее трудным моментом доказательства является установление того, что данная непрерывная на интервале функция имеет хотя бы какую-нибудь первообразную. Этот факт мы доказывать не будем. Пока же примем следующее: любая непрерывная на интервале функция имеет первообразную , т.е. .
1) Функция
![]() ,
где
,
где
![]() будет также являться первообразной,
так как
будет также являться первообразной,
так как
![]() .
.
Таким образом, выражение
,
где
какая-нибудь
первообразная на интервале
для
,
а
![]() произвольная
постоянная, охватывает все без
исключения первообразные для
.
Придавая различные численные значения
,
мы будем получать различные первообразные.
произвольная
постоянная, охватывает все без
исключения первообразные для
.
Придавая различные численные значения
,
мы будем получать различные первообразные.
2) Пусть
![]() и
и
![]() - две первообразные на интервале
для функции
,
т.е.
- две первообразные на интервале
для функции
,
т.е.
![]() и
и
![]() .
.
Тогда для любого имеем
![]()
по следствию из теоремы Лагранжа (если производная функции равна нулю на некотором промежутке, то функция постоянна на этом промежутке).
![]()
![]() ,
где
.
,
где
.
Определение 1.2. Совокупность всех
первообразных функций
,
где
для функции
называется неопределенным интегралом
от функции
и обозначается
![]() ,
т.е.
,
т.е.
![]() .
(1.1)
.
(1.1)
Здесь
называется подынтегральной функцией,
![]() подынтегральным
выражением,
подынтегральным
выражением,
![]() переменной
интегрирования, символ
переменной
интегрирования, символ
![]() знак неопределенного
интеграла.
знак неопределенного
интеграла.
Операция нахождения неопределенного интеграла от функции называется интегрированием этой функции. Правильность интегрирования всегда можно проверить дифференцированием результата. Заметим следующее: если производная от элементарной функции всегда является элементарной функцией, то первообразная от элементарной функции может оказаться и не представимой с помощью конечного числа элементарных функций.
График первообразной от функции называется интегральной кривой функции . Очевидно, мы получим любую другую интегральную кривую, если пере-

параллельном движении одной из них по вертикали.
