Контрольные вопросы и задания

1. Доказать теоремы 2, 3 для бесконечного числа множеств.

2. Доказать, что для любого отображения f выполняется включение f(A  B)  f(A)  f(B), а равенство будет только

тогда, когда f является биекцией.

3. Пусть A – произвольное множество из области определения отображения f. Верно ли равенство f ^-1(f(A)) = A?

4. Пусть B – произвольное множество из области значений отображения f. Верно ли равенство f(f ^-1(B)) = B?

Доказать тождества 5, 6.

5. f ^-1(A \ B) = f ^-1(A) \ f ^-1(B).

6. f(A)  B = f(A  f ^-1(B)).

7. Верно ли равенство f(A \ B) = f(A) \ f(B)? Если нет, то в какую сторону имеет место включение? При каких условиях выполняется тождество?

8. Доказать, что для любой функции f:

а) A  B  f ^-1(A)  f ^-1(B);

б) A  B   f(A)  f(B);

в) f(A) =   A  _а = ;

г) f ^-1(A) =   A  _а = .

9. Пусть  : A  B – взаимно однозначное соответствие. Доказать, что:

а)   ^-1 – взаимно однозначное соответствие между B и A;

б)   ^-1 o  = i; в)   o  ^-1 = i.

10. Доказать, что объединение (пересечение) двух отображений f₁ и f₂ из A в B является отображением из A в B тогда и только тогда, когда f₁ = f₂.

11. Доказать, что:

а) f(A)  B =    A  f ^-1(B) = ;

б) f(A)  B  A  f ^-1(B).

12. Пусть f : X  Y, g : Y  Z, h = g o f и B  Z. Тогда h ^-1(B) = f ^-1(g ^-1(B)).

4. Мощность множества

Одной из задач теории множеств является определение числа элементов множества и исследование вопроса о сравнении друг с другом двух множеств по количеству элементов.

Для конечных множеств самой разной природы эта задача легко решается непосредственным подсчетом. Для бесконечных – с помощью взаимно однозначного (биективного) отображения. Рассмотрим примеры построения такого отображения.

Задача 1. В качестве множества А рассмотрим интервал на числовой прямой, пусть А=(–1, 1), а в качестве множества В –множество действительных чисел R. Это множества одинаковой мощности, т.к отображение f(x) = tg(x/2), хА позволяет установить между ними искомое взаимно-однозначное соответствие.

Задача 2. Пусть А = [–1,1], В = (–1,1). Строим отображение f : A  B по следующему правилу: выделим в А последовательность –1, 1, 1/2, 1/3, 1/4, . . . , 1/n и положим f(–1)=1/2, f(1)=1/3, f(1/2)=1/4, f(1/3)=1/5, т.е. f(1/n) = 1/(n+2), а все точки, не входящие в эту последовательность отобразим сами в себя, т.е. f(x) = х. Следовательно, открытый и замкнутый интервалы эквивалентны.

Мощность – это то общее, что есть у любых двух эквивалентных множеств. Мощность множества A обозначается m(A) или |A|. Таким образом, m(A) = m(B), если A ~ B.

Если множество A эквивалентно какому-либо подмножеству множества B, то мощность A не больше мощности B (т.е. m(A)m(B)). Если при этом множество B не эквивалентно никакому подмножеству множества A, то m(A) < m(B).

Наименьшим среди бесконечных множеств является множество натуральных чисел  N.

ОПРЕДЕЛЕНИЕ. Назовем счетным всякое множество, эквивалентное множеству  N. Другими словами, счетным называется всякое множество, элементы которого можно перенумеровать или составить из них бесконечную последовательность.

Примеры счетных множеств.

1. Множество целых чисел Z={0, 1, 2, . . .}. Построим из его элементов последовательность: a₁ = 0; a₂= – 1; a₃ = 1; a₄ = –2; a₅ = 2;... Формулу для вычисления ее общего члена можно записать в виде

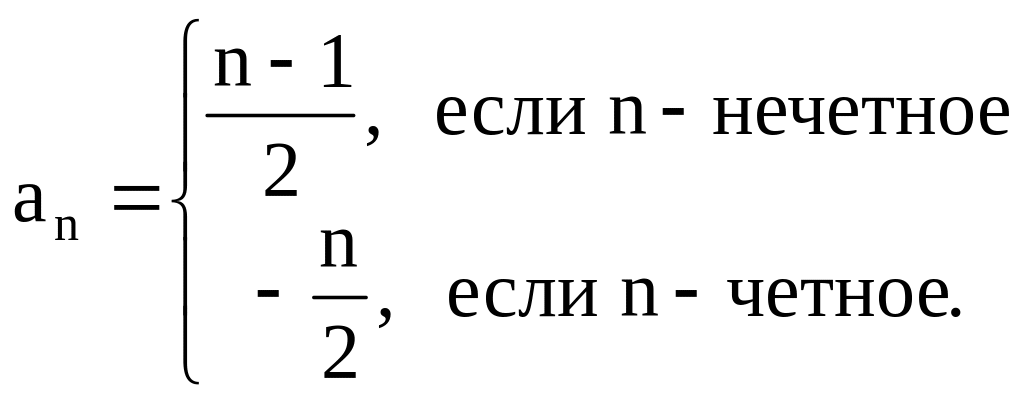
2. Множество Q всех рациональных чисел.

Задача 3. Установить взаимно однозначное соответствие между множеством всех последовательностей натуральных чисел и множеством всех строго возрастающих последовательностей натуральных чисел.

Решение. Рассмотрим произвольную последовательность натуральных чисел

n₁, n₂, . . . , n_k, . . .

Поставим ей в соответствие возрастающую последовательность

m₁< m₂< . . . < m_k< . . . ,

где m₁=n₁, m₂=m₁+n₂, . . . , m_k=m_k-1+n_k, . . . Легко видеть, что это соответствие - взаимно однозначное.

Задача 4. Доказать, что если A \ B ~ B \ A, то A ~ B.

Решение. Для произвольных множеств A и B справедливо равенство A =(A\B)(AB), где (A\B)(AB)=. Аналогично B= =(B\A)(AB), где (B\A)  (AB)=. Так как оба множества A и B являются объединением непересекающихся множеств, A\B~B\A по условию и (AB)~(AB), то A~B.

Задача 5. Доказать, что если расстояние между любыми двумя точками множества E на прямой больше единицы, то множество E конечно или счетно.

Решение. Разобьем прямую на счетное множество отрезков точками 0, 1, 2, 3, . . . Каждый отрезок содержит не более одной точки данного множества, следовательно, между точками множества E и некоторым подмножеством построенного множества отрезков существует взаимно однозначное соответствие. Значит, множество E не более чем счетно.

Задача 6. Доказать, что множество точек разрыва монотонной функции, заданной на [a, b], не более, чем счетно.

Решение. Каждая точка разрыва монотонной функции f(x) является точкой разрыва первого рода. Действительно, так как функция f(x) монотонна и ограничена на отрезке, то она имеет конечные пределы при x0, где  – произвольная точка разрыва функции f(x).

Назовем скачком функции в точке  разность f(+0) –f(–0) этих пределов. Пусть функция f(x) возрастает. Легко проверить, что множество точек разрыва, в которых скачок больше  (где  – произвольное положительное число), конечно, а число этих точек не больше, чем (f(b) – f(a)) /.

Обозначим через E_k множество точек разрыва со скачком, большим, чем 1/ k. Множество E всех точек разрыва равно объединению всех E_k: E = E₁  E₂  E₃  . . .  E_k  . . .

Так как все E_k конечны, то E не более чем счетно.

Для монотонно убывающей на [a, b] функции доказательство аналогично.

Задача 7. Доказать, что множество всех непрерывных функций на отрезке [a, b] имеет мощность континуума.

Решение. Рассмотрим множество Q всех рациональных точек отрезка [a,b], занумерованных произвольным образом, т.е. Q= ={r₁, r₂,...}. Поставим в соответствие каждой непрерывной на [a,b] функции f последовательность действительных чисел f(r₁), f(r₂),... Так как непрерывная функция на [a,b] полностью определяется своими значениями в точках множества Q, то тем самым устанавливается взаимно однозначное соответствие между множеством всех непрерывных функций на [a,b] и частью множества всех последовательностей действительных чисел. Значит, в силу результатов задач 11-13 п. 4, мощность множества всех непрерывных функций на [a,b] не больше мощности континуума. С другой стороны, она не может быть меньше мощности континуума, так как все функции, постоянные на [a,b], уже образуют множество мощности континуума. Для завершения доказательcтва остается применить теорему Кантора-Бернштейна (см. п.4).