Планиметрия

Упражнение №1*.

Найдите способ двумя прямолинейными разрезами разрезать произвольный треугольник на части, из которых можно сложить равнобедренный треугольник.

Упражнение №2.

С А и СВ – касаются окружности в точках А и В соответственно, АD –её диаметр. Прямые DВ и АС пересекаются в точке Е. Докажите, что С – середина отрезка АЕ. Упражнение №3. В угол АВС вписана окружность, которая касается его в точках А и С. Прямая, проведённая из А параллельно стороне ВС пересекает окружность в точке D.

Прямая ВD пересекает окружность в точке Е.

Прямая АЕ встречает сторону ВС угла АВС в точке F.

Доказать, что BF=FC. Упражнение №4.

Могут ли 4 точки на плоскости быть вершинами разных четырёхугольников?

Упражнение №5. Приведите пример 10-угольника, все стороны которого лежат на 5 прямых.

Площадь.

Def. Площадью (временно) назовём неотрицательную аддитивную функцию S, определённую на некоторых подмножествах плоскости и обладающую следующими свойствами:

1. Площадь квадрата со стороной 1 равна 1;

2. Площади конгруэнтных фигур равны;

3. Если у каждой из двух фигур А и В имеется площадь и они не имеют общих внутренних точек, (то есть, точек, являющихся центрами кругов, целиком содержащихся внутри фигуры), то S(AB)=S(A)+S(B).

Иными словами, если две фигуры вообще не пересекаются или имеют только общую границу, то их площади складываются (площадь фигуры равна сумме площадей частей, из которых она составлена).

Фигуры, имеющие одинаковую площадь, называются равновеликими.

Исходя из этого определения и предполагая, что у всех ниже названных фигур площади существуют, докажите, что

Упражнение №6.

1. Площадь параллелограмма равна произведению любой его стороны на высоту, опущенную на неё из противоположной её стороны;

2. Площадь треугольника равна половине произведения любой его стороны на высоту, опущенную на неё из противолежащей ей вершины треугольника;

3. Б иссектриса делит сторону треугольника на отрезки в отношении, равном отношению прилежащих к этим отрезкам боковых сторон: АЕ:ЕС=с:а.

4. Д иагонали трапеции делят её на 4 треугольника с точкой пересечения этих диагоналей в качестве общей вершины. Треугольники, имеющие сторонами боковые стороны трапеции, равновелики.

5. Дан треугольник АВС. Найдите ГМТ М плоскости, таких, что треугольники АМС и ВМС равновелики.

6. Площадь трапеции равна произведению полусуммы её оснований на её высоту.

Упражнение №7.

Докажите теорему о пропорциональных отрезках из предыдущего конспекта для случая несоизмеримых отрезков.

Барицентр (центр масс)

Def. Материальной точкой mA называется пара (m,A), где А – точка пространства, a m – число. M называют массой, сосредоточенной в А. Точка М называется центром масс или барицентром системы материальных точек {m₁A₁, m₂A₂,…,m_nA_n}, где m₁+m₂+…+m_n0 если выполняется векторное равенство:

Упражнение №8. Барицентр М системы материальных точек {m₁A₁, m₂A₂,…,m_nA_n} однозначно определяется следующим характеризующим свойством: если N – любая другая точка пространства, то

Упражнение №9 (Теорема о существовании и единственности барицентра). Для любой системы материальных точек {m₁A₁, m₂A₂,…,m_nA_n} с ненулевой суммарной массой m=m₁+m₂+…+m_n барицентр М всегда существует и единственен.

Упражнение №10. (Теорема о суперпозиции операции нахождения барицентра) Пусть М – барицентр системы материальных точек {m₁A₁, m₂A₂,…,m_nA_n}. Пусть Т – барицентр подсистемы {m₁A₁, m₂A₂,…,m_kA_k}, где kn и m₁+m₂+…+m_k0.

Тогда М является также барицентром для системы {(m₁+m₂+…+m_k)Т, m_k+1A_k+1, m_k+2A_k+2,…,m_nA_n}

Последовательным применением упражнения 10 можно легко получить следующее утверждение, служащее техническим инструментом решения многих практических задач.

Упражнение №11. Пусть имеется система S материальных точек {m₁A₁, m₂A₂,…,m_nA_n}. Можно произвольным образом разбить эти точки на группы S₁,…,S_k и заменить каждую группу её центром масс T_i с массой M_i, равной сумме масс точек этой группы (при условии, что она не равна нулю!) и взять центр масс полученной новой системы {M₁T₁,…,M_kT_k}.

Он будет совпадать с центром масс исходной системы S. Упражнение №12.

Докажите «правило рычага»: центр масс системы из двух точек {m₁A₁, m₂A₂} находится на отрезке [A₁,A₂] в точке , определяемой архимедовым правилом: m₁d₁=m₂d₂.

Упражнение №13.

Используя упражнение 9, докажите заново теорему о том, что медианы треугольника пересекаются в одной точке и делятся в этой точке в соотношении 2:1, считая от вершины.

Упражнение №14.

Через вершину В треугольника АВС и через середину медианы АМ проведена прямая. В каком отношении она делит сторону АС?

Упражнение №15.

1. Соединим каждую из вершин тетраэдра с точкой пересечения медиан противолежащей грани. Можно ли утверждать, что полученные 4 отрезка пересекутся в одной точке?

2. Соединим середины противоположных рёбер тетраэдра. Можно ли утверждать, что полученные 3 отрезка пересекутся в одной точке?

Упражнение №16.

1. В вершинах А, В, С, D параллелограмма помещены массы p, q, p, q соответственно. Докажите, что центром масс служит центр параллелограмма.

2. В вершинах А, В, С, D параллелограмма помещены такие массы m_A, m_B, m_C, m_D, что центр масс совпадает с центром параллелограмма. Докажите, что m_A=m_C и m_B=m_D.

Упражнение №17.

Пусть f – линейное преобразование пространства, f(A_i)=B_i., i=1,…,n. Пусть Z_A – центр масс системы материальных точек {m₁A₁, m₂A₂,…,m_nA_n}, Z_B – центр масс системы материальных точек {m₁В₁, m₂В₂,…,m_nВ_n}. Докажите, что

1. f(Z_A)=Z_B;

2. .

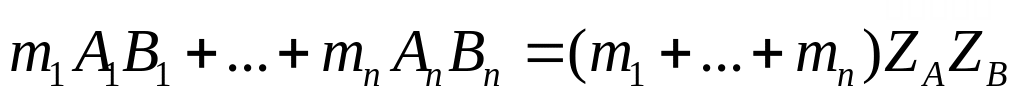3. Пусть f – такое преобразование, при котором система {m₁A₁, m₂A₂,…,m_nA_n} в целом переходит в себя, т.е., {m₁f(A₁), m₂f(A₂),…,m_nf(A_n)}совпадает с точностью до порядка с исходной системой. Докажите, что в этом случае ц.м. является неподвижной точкой, т.е., f(Z)=Z.

Упражнение №18.

Пусть Z и Z - центры масс треугольников ABC и ABC соответственно.

Докажите, что . Упражнение №19.

1. Докажите, что если многоугольник А₁А₂…А_n переходит в себя при повороте вокруг точки О на угол , 0<<2, то

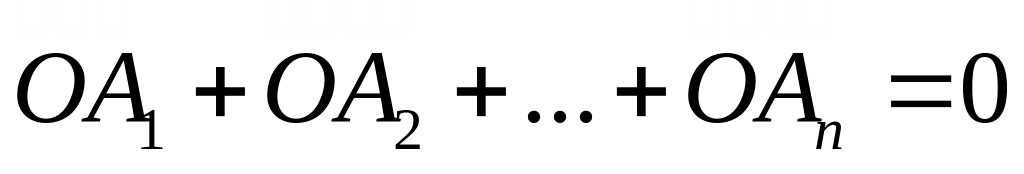
2. Докажите, что центроид правильного пятиугольника совпадает с центром его описанной окружности.

3. Докажите, что центроид правильного тетраэдра совпадает с центром его описанной сферы.

Упражнение №20.

1. Докажите, что если все материальные точки системы лежат в некоторой плоскости, то и их центр масс лежит в этой плоскости.

2. Докажите, что если все материальные точки системы лежат на некоторой прямой, то и их центр масс лежит на этой прямой.

3. Докажите, что если система материальных точек переходит в себя при симметрии относительно плоскости , то её центр масс лежит в плоскости .

4. Докажите, что если конечная система материальных точек переходит в себя при повороте вокруг некоторой прямой  на угол , 0<<2, то центр масс этой системы лежит на прямой .

Упражнение №21.

1. Многогранник называется транзитивным, если для любой пары (А,В) его вершин найдётся движение, переводящее А в В и весь многогранник при этом переходит в себя. Докажите, что транзитивный многогранник является вписанным в сферу, центр которой является центроидом этого многогранника.

2. Докажите, что если многогранник А₁А₂…А_n транзитивен и О – центр его описанной сферы, то .

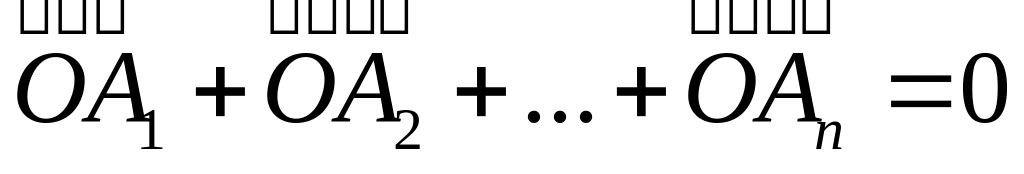Упражнение №22.

АВСD – квадрат со стороной а. На каком расстоянии от центра квадрата находится точка Р, если

Упражнение №23.

Средней линией четырехугольника называется отрезок, соединяющий середины его противоположных сторон. Докажите, что точка пересечения двух средних линий является центроидом четырехугольника 1А, 1В, 1С, 1D.

Упражнение №24.

1. Докажите, что центр масс трёх материальных точек, расположенных в вершинах треугольника всегда находится строго внутри этого треугольника;

2. Докажите, что любая внутренняя точка треугольника является центром некоторых масс, помещенных в вершинах этого треугольника;

3. Докажите, что при любом выборе точки Р внутри треугольника возможно и при этом единственным способом так распределить по его вершинам единичную массу, чтобы центром масс полученных материальных точек оказалась точка Р.

Упражнение №25.

В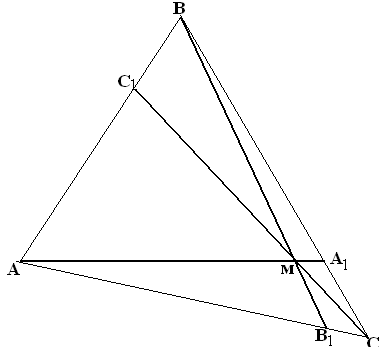 треугольнике АВС проведены отрезки АА₁, ВВ₁ и СС₁, пересекающиеся в точке М. Пусть |AC₁|:|C₁B|=p, |AB₁|:|B₁C|=q.

Докажите формулу Ван-Обеля: |AM|:|MA₁|=p+q. Упражнение №26.

С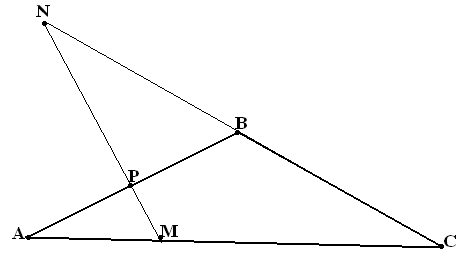 торону СВ треугольника АВС продолжили за вершину В на такое же расстояние: СВ=BN. Точка М делит сторону АС в отношении 1:2 считая от вершины А: |МС|=2|АМ|. В каком отношении делит точка Р пересечения отрезков АВ и NМ эти отрезки?

(Hint: distribute masses in points A, C and N so, that mass centre of system (m₁A, m₂C, m₃N) will be in point P)

Упражнение №27*.

В треугольнике ABC точка F делит сторону BC в отношении 3:1, считая от вершины B. Точки M и P делят стороны AB и AC в отношении 1:5, считая от вершин A и C с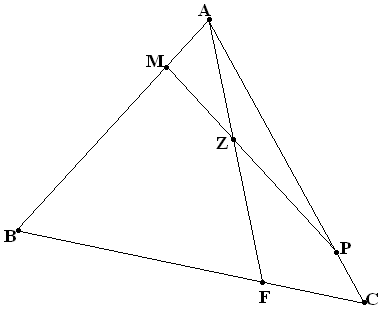 оответственно. В каком отношении делит точка Z пересечения отрезков MP и AF эти отрезки?

(Hint: consider system S=(m₁A, m₂A, m₃B, m₄C) with masses distributed so, that Z becomes mass centre of the system)

У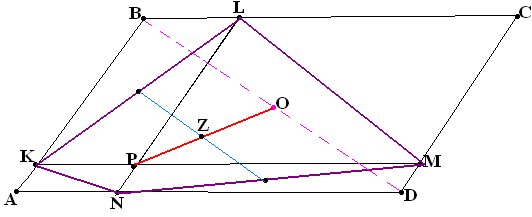 пражнение №28*.

Через точку Р, расположенную внутри параллелограмма ABCD, проведены прямые, параллельные его сторонам. Их точки пересечения со сторонами параллелограмма ABCD образуют четырехугольник KLMN. Обозначим точку пересечения средних линий четырехугольника KLMN за Z, а центр параллелограмма ABCD за O. Докажите, что ZPO и найдите отношение, в котором она делит этот отрезок.

( Hint: put masses in vertices of KLMN to make Z their mass centre. Then apply #14 to KBLP and NPMD).

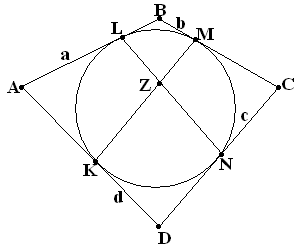
Упражнение №29.

Окружность, вписанная в четырехугольник ABCD, касается его сторон в точках K, L, M и N. Этими точками стороны четырехугольника ABCD разбиты на отрезки с длинами a, b, c и d, как показано на рисунке. В каком отношении делятся отрезки KM и LN их точкой пересечения Z?

Упражнение №30.

Докажите, что точка пересечения средних линий и середины диагоналей четырехугольника лежат на одной прямой.

Упражнение №31.

В треугольнике ABC точка М – середина медианы ВВ₁. В каком отношении прямая АМ делит медиану СС₁?

Упражнение №32.

П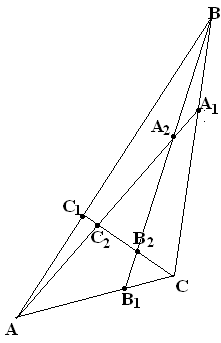 усть стороны АВ, ВС и АС треугольника ABC имеют длины c, a и b соответственно. Докажите, что центром масс системы {аА, bB, cC} служит центр вписанной окружности.

Упражнение №33.

.

Найдите отношение площади треугольника A₂B₂C₂ к площади треугольника АВС. Упражнение №34.

П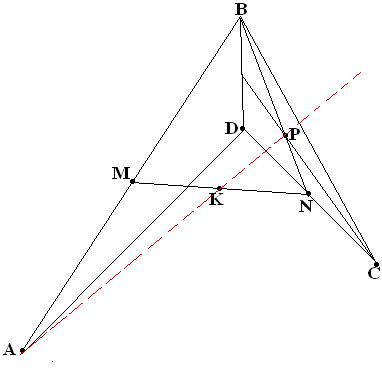 усть среди точек A, B, C и D никакие три не инцидентны одной прямой. Пусть M – середина АВ, N – середина CD, K – середина MN, а P – точка пересечения медиан треугольника BCD.

Докажите, что точки А, К и Р инцидентны одной прямой.

Как это часто бывает в математике, понятие центра масс (или барицентра) возникло из механики, где массы материальных точек по смыслу являются положительными числами. Однако, ни в самой математической модели, ни в доказательствах теорем №№6-9, на основе которых решались все последующие задачи, это ограничение никак не предполагалось, на него мы нигде не опирались и его нигде не использовали.

Более того, как раз введение отрицательных масс бывает во многих случаях удобно.

Упражнение №35.

П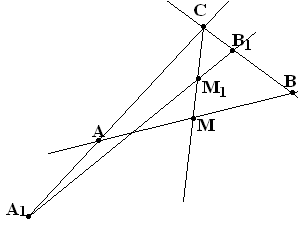 рямая l пересекает прямые СА, СВ и медиану СМ в точках А₁, М₁ и В₁ так, что СА=рСА₁, СВ=qCB₁ и CM=rCM₁. Выразить r через p и q.

(Distribute masses to make M₁ mass centre. To that end, put 1A and 1A and then add m₁C and m₂C to make A₁ mass centre of {m₁C, 1A} and B₁ mass centre of {m₂C, 1B})

Следующая теорема играет важную роль в проективной геометрии.

Упражнение №36*.

Дан четырехугольник АFМE. C=AFME, B=AEFM, P=AMEF, Q=AMBC. Н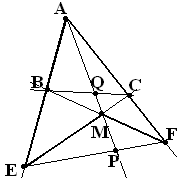 айти двойное отношение (anharmonic ratio) .

(Chose b, c to make Q mass centre of {bB, cC}. Put a into A to make M mass centre of {aA, (b+c)Q}. Prove, that E is at the same time mass centre of {aA, bB} and F – of {aA, cC}. Prove, afterwards, that P is mass centre of {aA, bB, aA, cC} and derive from this identity (a+b+c) +a = . Notice, that M at the same time is a mass centre of {aA, (b+c)Q} and conclude that anharmonic ratio sought equals -1}).

Def. Двойным, сложным или ангармоническим отношением четырёх р азличных точек А, В, С и D, инцидентных одной прямой, называется частное двух простых отношений:

(A, B, C, D)= . Если (A, B, C, D)=-1, то четвёрка A, B, C, D называется гармонической.

Упражнение №37.

Докажите, что точка пересечения боковых сторон трапеции, точка пересечения её диагоналей и середины оснований лежат на одной прямой.

Далее следуют две важные теоремы, часто применяемые в планиметрии. Их следует запомнить.

Упражнение №38*. (Теорема Чевы¹)

Дан треугольник АВС и точки А₁, В₁, С₁ на прямых ВС, СА и АВ соответственно.

Т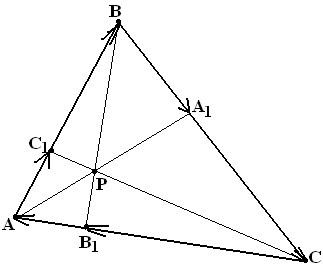 огда 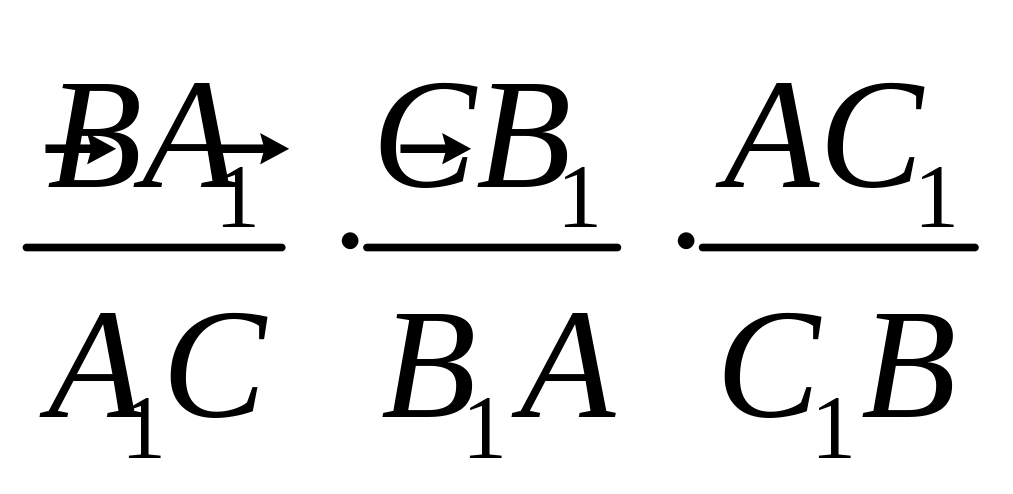=1  Либо прямые АА₁, ВВ₁ и СС₁ конкуррентны (инцидентны одной точке), либо все три параллельны.

( Let AC₁=C₁B, BA₁=A₁C, CB₁=B₁A.

Notice, -1,-1, -1. Also, =1.

Consider {1A, B}, {B, C} and {C, 

Separately treat cases 1++0 and 1++=0)

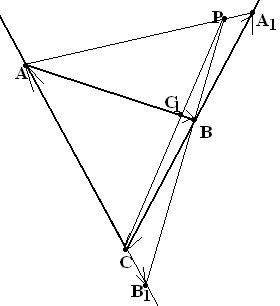
Упражнение №39*. (Теорема Менелая²)

Дан треугольник АВС и точки А₁, В₁, С₁ на прямых ВС, СА и АВ соответственно.

Тогда =-1  точки А₁, В₁, С₁ инцидентны одной прямой.

(follow the way, shown in the previous exercise and notice, that -1,-1, -1 and 0,0, 0) У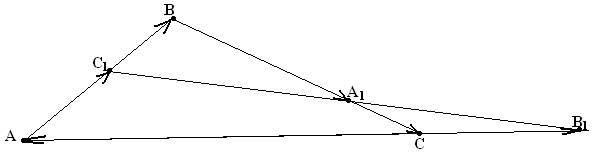 пражнение №40.

Пусть АВСD – параллелограмм. Докажите, что центром масс системы {mA, -mB, mC} является четвёртая вершина D, т.е., в сокращённых обозначениях, mA-mB+mC=mD.

Упражнение №41.

Четырехугольник ABCD вписан в окружность. Через середины его сторон проведены прямые, перпендикулярные противоположным его сторонам. Докажите, что все они пересекаются в одной точке.

(Hint: consider system {1A, 1B 1C, 1D, (-2)O} where O is the centre of the circumference)

Упражнение №42**. (Теорема Ньютона)

Четырехугольник ABCD описан около окружности. Докажите, что её центр лежит на отрезке, соединяющем середины диагоналей этого четырехугольника.

(Hint: Let F=ADBC. Prove, that O is barycentre of {m₁A, m₂B, m₃F} where m₁=|BF|, m₂=|AF| and m₃=|AB|. As well as barycentre of {m₄C, m₅D, m₆F} where m₄=-|DF|, m₂=-|CF| and m₆=|CD|. Prove then that F is barycentre of {m₁C, m₅B} as well as { m₄A, m₂D}. Then regroup, keeping in mind that m₃+m₆= m₃+m₂ +m₄+m₅)

Упражнение №43.

Четырехугольник ABCD описан около окружности. В каждой точке касания окружности и стороны четырехугольника помещена масса, равная длине этой стороны. Докажите, что центром масс этой системы служит центр окружности.

Упражнение №44.

Окружность, вписанная в треугольник АВС, касается его сторон в точках C₁, A₁ и B₁ соответственно. Докажите, что прямые АА₁, ВВ₁ и СС₁ конкуррентны.

Упражнение №45.

Заново, с помощью теоремы Менелая, докажите уже хорошо известный вам факт. Основания перпендикуляров, опущенных из точки окружности, описанной около треугольника, на прямые, содержащие его стороны, инцидентны одной прямой (прямой Симсона).

Следующее упражнение – часто используемая теорема.

Упражнение №46.

Докажите, что AC=2RsinABC, где R – радиус окружности, описанной около треугольника АВС.

Упражнение №47.

Пусть O₁– центр вписанной окружности треугольника АВС, B₁ – точка пересечения биссектрисы треугольника ABC , проведённой из вершины B , с описанной окружностью.

Докажите, что треугольник O₁B₁C – равнобедренный.

Докажите теорему теорему трилистника (теорему И. Кушнира):

Пусть I – инцентр треугольника АВС, AW – биссектриса. Тогда WC=WI=WB.

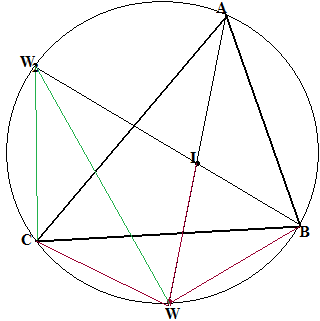
Упражнение №48.

Докажите формулу Эйлера: = R² - 2rR , где O₁ , O₂ – центры соответственно вписанной и описанной окружностей треугольника, r , R – радиусы этих окружностей.

Упражнение №49

Обоснуйте следующую формулу площади треугольника АВС: S(ABC)=|AB||AC|sinBAC.

Упражнение №50*.

Докажите, что если две биссектрисы треугольника равны, то он равнобедренный.

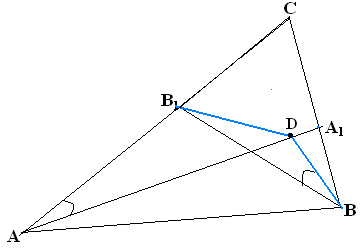( one method is shown on a picture: attach half of angle A to BB₁ and notice, that ABDВ₁ is inscribed. Rely on #46. )

Упражнение №51*.

Докажите, что если четырёхугольник вписан в окружность, то сумма произведений длин двух пар его противоположных сторон равна произведению длин его диагоналей.

(use #45 and 46)

Упражнение №52.

Диагонали выпуклого четырёхугольника взаимно перпендикулярны. Докажите, что четыре проекции точки пересечения диагоналей на стороны четырёхугольника лежат на одной окружности.

Упражнение №53.

Докажите, что для любого треугольника проекция диаметра описанной окружности, перпендикулярного одной стороне треугольника, на прямую, содержащую вторую сторону, равна третьей стороне.

Упражнение №54.

Докажите, что если диагонали вписанного четырёхугольника перпендикулярны, то середины его сторон и основания перпендикуляров, опущенных из точки пересечения его диагоналей на стороны, лежат на одной окружности.

Построить с помощью одной линейки!³

Упражнение №55*.

И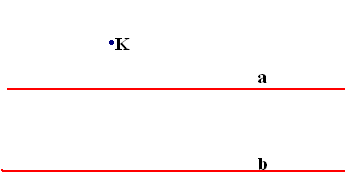 меются две параллельные прямые, а и b. Через данную точку К, не инцидентную этим прямым, провести прямую, параллельную им. Построение обосновать.

Упражнение №56*.

Дан отрезок ВС, и на нём отмечена его середина, точка М.

Д ана точка N, не инцидентная прямой ВС.

Провести через неё прямую, параллельную ВС.

Построение обосновать.

Изогональное соответствие⁴.

Def. Прямые, симметричные относительно биссектрисы треугольника (инцидентные той же его вершине) называются изогональными. Если при этом одна из этих прямых – высота, то прямые называются ортоизогональными.

Упражнение №57.

Прямая изогональна выоте треугольника  она содержит диаметр описанной окружности треугольника.

Упражнение №58.

Пусть О - центр окружности, описанной около треугольника АВС, Н₂ и Н₃ – основания высот, проведённых из вершин В и С соответсвенно. Докажите, что ОА Н₂Н₃.

Упражнение №59.

Что можно сказать о треугольнике, у которого медиана и высота, проведённые из одной вершины, изогональны?

Упражнение №60.

Определите углы треугольника у которого биссектриса, медиана и высота, проведённые из одной вершины, делят угол на 4 равные части.

Упражнение №61.

Определите углы треугольника у которого медиана и высота, проведённые из одной вершины, делят угол на 3 равные части.

Упражнение №62.

Пусть ХВС, M и N – проекции Х на стороны AC и AB соответственно, а АН₁ – высота.

Тогда А, М, Х, Н₁ и N лежат на одной окружности.

Чтобы эта окружность и окружность, описанная около треугольника АВС касались, необходимо и достаточно, чтобы отрезки АХ и АН₁ были ортоизогональны.

Упражнение №63.

В обозначениях предыдущего упражнения, АХ и АН₁ ортоизогональны  MN||BC.

Упражнение №64*.

В обозначениях предыдущего упражнения, если АХ и АН₁ ортоизогональны, то площадь треугольника АВС S=0,5AA₀×MN, где А₀ – точка пересечения прямой АН₁ и окружности, описанной около треугольника АВС.

(Hint: this is an area of a quadrilateral MANA₀. XMA₀. Think of a homothetic transformation from A as its centre.)

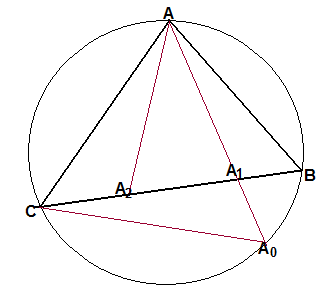
Упражнение №65.

Опишем окружность около треугольника АВС и пусть отрезки АА₂ и АА₁ изогональны. Тогда имеем две пары подобных треугольников: АВА₀ и АСА₂; САА₀ и А₂АВ.

Упражнение №66*.

Пусть длины сторон АС и АВ треугольника АВС равны b и c соответственно.

Пусть длины отрезков, на которые биссектриса АL₁ делит сторону ВС равны m и n соответственно. Тогда длина биссектрисы АL₁ равна .

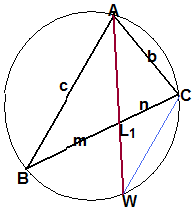
(Hint: remember the identity mn=AL₁L₁W and use the previous exercise)

Упражнение №67*.

Пусть W – точка пересечения биссектрисы АL₁ с окружностью, описанной около треугольника АВС, M и N – проекции точки L₁ на стороны АС и АВ соответственно. Тогда площадь треугольника АВС S=0,5AWMN.

( Hint: from similarity get l_aAW=bc and time both sides by sinA)

Упражнение №68.

Пусть ХВС, M и N – проекции Х на стороны AC и AB соответственно, F лежит на окружности, описанной около треугольника АВС и прямые АХ и АF изогональны. Тогда S_ABC=0,5AFMN.

Упражнение №69*. (Теорема Птолемея)

Пусть a, b, c, d – стороны вписанного четырехугольника, d₁ и d₂ – его диагонали.

Тогда аc+bd= d₁d₂.

(Hint: consider two pairs of similar triangles: ABCAA₂D and DACAA₂B)

Разные задачи⁵

Упражнение 70*.

К двум, пересекающимся в точках M и N окружностям радиусов R и r, провели общую касательную. Через две этих точки касания и одну из точек пересечения (M или N) провели окружность. Найдите её радиус.

( AN=2Rsin, BN=2rsin, express the sought radius via ex.46 using angles A and B) Упражнение №71.

В одной полуплоскости от прямой АС расположены точки В и D. В треугольники ABC и CDA вписаны окружности.

Найдите длину общей внешней касательной к ним в случаях, когда

а) АВ=5, ВС=7, CD=DA;

b) AB=7, BC=CD, DA=9. P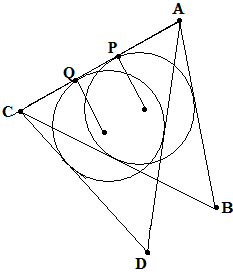 rove and use (PQ=AQ-AP) the following fact: the length of a tangent AP to the circumference, inscribed into triangle ABC is equal to p-a where a=|BC| and p is a half of the perimeter of the triangle ABC) Упражнение №72.

На отрезке АС длины а взяли произвольную точку В и провели через неё прямую под углом  к прямой АС. На этой прямой взяли произвольную точку М. Найдите расстояние между центрами окружностей, вписанных в треугольники МАВ и МВС.

Упражнение №73.

На гипотенузе прямоугольного треугольника с суммой длин катетов, равной а, во внешнюю сторону построен квадрат. Найдите длину отрезка, соединяющего вершину прямого угла с центром квадрата, и углы, которые он образует с катетами треугольника.

Упражнение №74*.

Пусть R и r – радиусы описанной и вписанной окружностей треугольника.

Докажите, что R2r.

(Find the circumference which intersects sides of a triangle with radius exactly equal 0,5R)

Упражнение №75.

Докажите, что вписанная и описанная сферы существуют для любого тетраэдра.

Пусть их радиусы R и r соответственно. Докажите, что R3r.

Упражнение №76.

Докажите, что точка, симметричная ортоцентру относительно стороны треугольника, лежит на описанной окружности.

Упражнение №77.

Ортоцентр равнобедренного треугольника лежит на его вписанной окружностиё Найдите углы треугольника. (Используйте предыдущее упражнение и теорему трилистника)

Упражнение №78.

Пусть Н – ортоцентр треугольника АВС и СН=АВ. Найдите угол С,

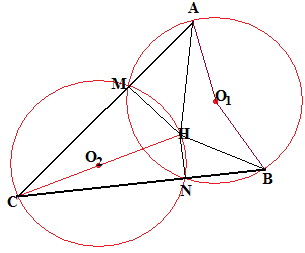( Build circumferences on CH and AB as diameters. So, AO₁B – straight line by construction. Prove, that AHN and BHN are also straight lines, where H is an orthocenter.)

Упражнение №79.

Д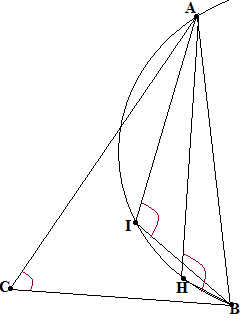 ано, что ортоцентр Н треугольника АВС, его инцентр I, вершины В и А лежат на одной окружности. Найдите угол С.

Следующее упражнение служит подготовительной леммой для решения следующей за ней задачи о пирате, хотя важна и сама по себе (для физики).

Упражнение №80.

П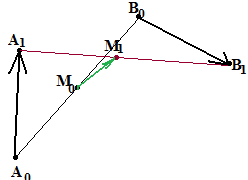 усть за время t точка А₀ передвинулась в положение А₁ на вектор А₀А₁=v₀, a точка В₀ передвинулась в положение В₁ на вектор В₀В₁=v₁. На какой вектор передвинется середина отрезка А₀В₀? Иными словами, если М₀ – середина А₀В₀ а М₁ – середина А₁В₁, то чему равен вектор ? Естественно, вектора здесь «свободные», т.е., не прикреплённые к одной общей точке: отрезки AD и BC пересекаются и делятся их общей точкой пополам. Это определение включает в себя как случай параллелограмма ABDC, так и случай «вырожденного параллелограмма», когда все четыре точки A, B, C, D инцидентны одной прямой.

Упражнение №81*.

Пирату, после многих лет поисков и приключений, удалось, наконец, раздобыть карту с описанием места, где зарыт клад. На необитаемом острове, рядом с местом, где зарыт клад, росло три дерева – сосна, дуб и берёза. Инструкция гласила:

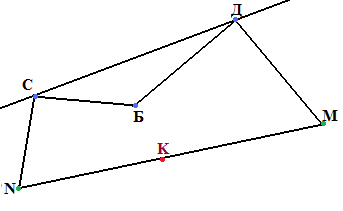« Встань под берёзой и ступай к дубу, считая шаги. Дойдя до дуба, поверни под прямым углом направо и иди на такое же расстояние, какое прошёл. Пройдя его, забей там колышек и вернись к берёзе. Теперь иди к сосне, считая шаги. Дойдя до сосны, поверни под прямым углом налево и иди на такое же расстояние, какое прошёл. Пройдя его, забей и там колышек. Ровно посередине между колышками зарыт клад.» Прибыл пират на остров, нашёл дуб и сосну, а берёзы и след простыл. Даже пня от неё не осталось.

Присел пират, пригорюнился и призадумался. Если бы учился он в школе геометрии, то нашёл бы клад. А как?