14

Построение . Элементарные функции.

Сейчас мы пройдём стандартным и самым простым путём, приспособленным именно для вещественных чисел, и использующим линейную упорядоченность Q. Желающие могут прочесть это в любом вузовском учебнике по математическому анализу. Возможно, в будущем мы построим R ещё и другим, более трудным, но и более универсальным способом.

Необходимость расширения понятия числа возникает в связи с характером решаемых задач. Если бы человечество ограничилось одной операцией сложения, то целых чисел было бы достаточно (а натуральных всё-таки не хватило бы, так как не всякое уравнение а+х=b, а,b имеет решение в натуральных числах). Операция умножения уже заставляет присоединить к целым числам дроби – решения уравнений АХ=В, А, В, А0. Оказывается, однако, что полученное множество Q, названное нами рациональными числами, уже замкнуто не только относительно операций сложения и умножения, но и относительно разрешимости обратных к ним операций вычитания и деления. Если ограничиться только задачами, в которых неизвестные величины связаны линейными зависимостями, т.е. задачами, приводящими к системам линейных уравнений, то никаких новых чисел не понадобится. А именно, либо система 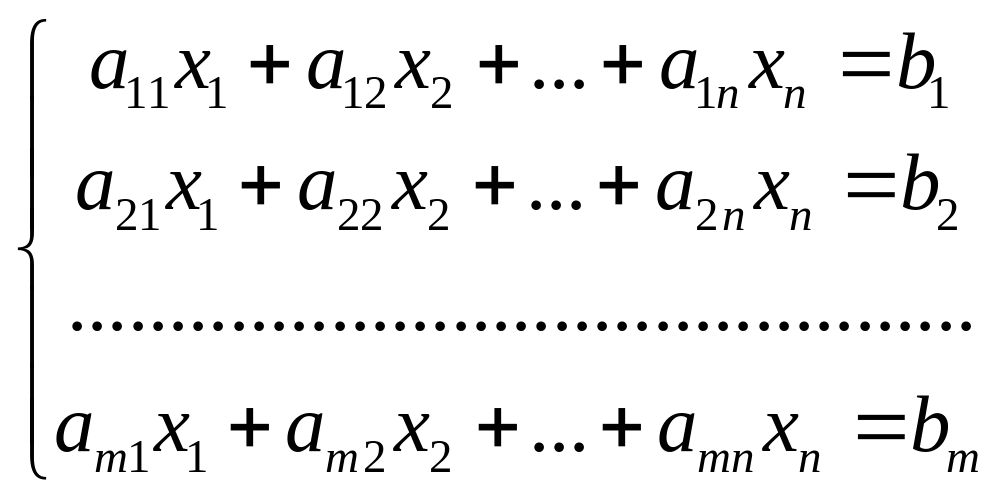с рациональными коэффициентами (все a_i,j и b_kQ) вообще не имеет решений (т.е., противоречива), либо она имеет рациональное решение (в Q).

Упражнение 1. Докажите это.

Но встречаются задачи, в которых зависимость не линейна. Исторически, первыми с этой проблемой столкнулись греки (возможно, на самом деле – египтяне, у которых греки многому научились). Докажите теорему Пифагора:

Упражнение 2. Площадь квадрата, построенного на гипотенузе прямоугольного треугольника равна сумме площадей квадратов, построенных на его катетах. 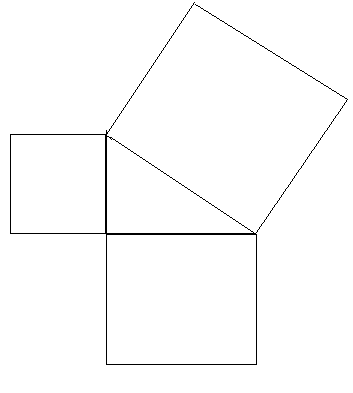Существуют десятки разных доказательств этой важнейшей теоремы евклидовой геометрии, благодаря которой мы имеем возможность измерять расстояния между двумя точками.

Но это означает, например, что квадрат гипотенузы равнобедренного прямоугольного треугольника с катетами, равными единице, равен двум.

Упражнение 3. Докажите, что не существует рационального числа, квадрат которого был бы равен двум.

(hint: assume it does exist, such a that 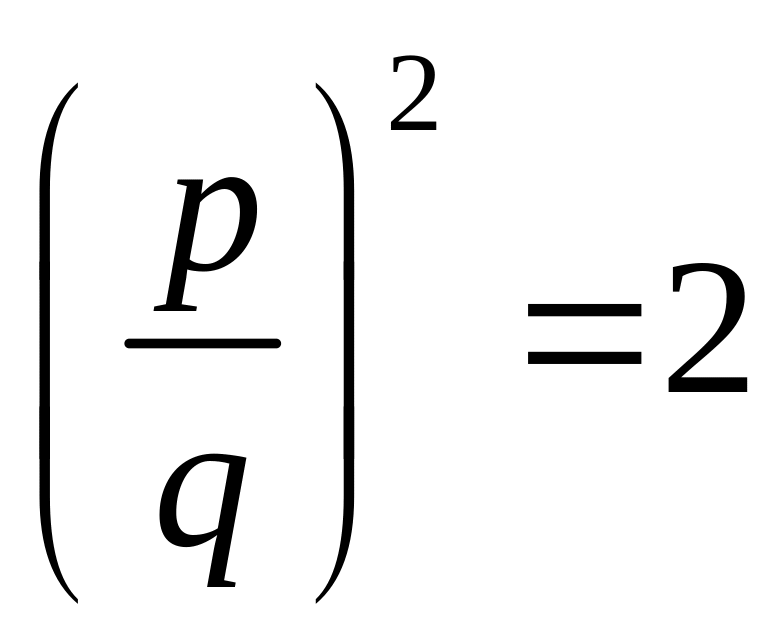and bring it to the contradiction with the assumption that (p,q)=1).

Упражнение 4. Точно таким же приёмом обобщите это на случай уравнения х²=m, когда число m имеет в разложении на простые множители хотя бы один множитель в нечётной степени.

Таким образом, либо уравнение х²-а=0, а имеет решение в Z, либо оно не имеет его не только в Z, но и в Q.

Задумаемся, что означает, что длина гипотенузы упомянутого треугольника не измеряется рациональным числом. Если у нас имеются два отрезка с длинами и соответственно, то их обоих можно измерить третьим отрезком длины, например, . Он поместится ровно np раз в первом отрезке и mq раз во втором. В случае же, с которым мы столкнулись, такого отрезка, – которым можно было бы измерить и катет и гипотенузу, - нет. Такие отрезки, поэтому, и называются несоизмеримыми. Упражнение 5. Докажите, что в области Q⁺ (неотрицательных рациональных чисел) функция у=х² монотонно возрастает (в Q^-, соответственно, монотонно убывает).

Упражнение 6. Выведите отсюда, что всё множество Q разбивается на два непустых подмножества А и В таких, что: А={qQ|(q<0)(q²<2)} и B={qQ|(q>0)(q²>2)}, причём а,b aA, bB имеет место a<b.

Упражнение 7*.

Докажите, что в А нет наибольшего числа (аналогично, в В нет наименьшего).

(of course, assume the opposite and find h<1 for p=max{q| q²<2} such, that (p+h)²<2)

Тем самым, как вы видите, на числовой прямой есть «свободные места» для точек х>0, претендующих на свойство х²=2, а именно, между множествами А и В. Однако, зазор между А и В оставляет место только для одной такой точки, ибо рациональные числа «плотно» распределены вдоль числовой прямой.

Упражнение 8. Докажите, что n а,b aA, bB такие, что .

Поэтому, в «щель» между А и В можно поместить только одно такое “число”. Его мы и назовём «корнем из двух» и обозначим как 2.

Def. Такое разбиение множества рациональных чисел называется Дедекиндовым сечением. Итак, Дедекиндовым сечением называется разбиение множества Q рациональных чисел на два непустых подмножества А и В таких, чтоа,b aA, bB a<b.

Множество В может при этом иметь наименьшее число, такое сечение будет рациональным, определяемым этим самым наименьшим элементом В - рациональным числом. Например, А={qQ, q<2} и B={qQ, q2}.

Тогда АВ=Q, АВ=; а,b aA, bB a<b. В А, как и ранее, нет наибольшего, но в В на этот раз есть наименьшее – 2. Таким образом, имеются два типа сечений – рациональные и иррациональные.

Итак, мы построили новые объекты – сечения, некоторое подмножество которых отвечает рациональным (старым) числам, а новые элементы послужат для расширения понятия числа, для пополнения их новыми «числами». Программа довольна прозрачна: надо сначала научиться их сравнивать (перенести на них отношение порядка, превратив в упорядоченное множество); затем естественным образом определить сложение и умножение и доказать, что они удовлетворяют обычным свойствам (коммутативность, ассоциативность, дистрибутивность); затем убедиться в том, что операции сложения и умножения согласованы с отношением порядка и, наконец, что в полученном упорядоченном поле рациональные сечения образуют подполе, изоморфное полю рациональных чисел. Приступим к её реализации.

Поскольку одно множество в разбиении АВ=Q однозначно определяет второе (оно просто является его дополнением во множестве рациональных чисел Q), то будем в дальнейшем называть сечением множество А (элементы А называются нижними числами сечения (А,В), а элементы В – верхними). Соберём воедино все свойства этого А:

Def. Множество А рациональных чисел называется сечением, если оно

1. Не пусто и не равно всему Q;

2. Содержит вместе с каждым своим числом и все, меньшие его числа;

3. Не имеет наибольшего числа.

Очевидно, что

Упражнение 9. Если А – сечение, рА, а qA, то p<q.

Упражнение 10. Пусть rQ, r*={pQ p<r}. Тогда r* – сечение, а r – его наименьшее верхнее число.

Т.о., рациональные сечения характеризуются наличием наименьшего числа во множестве В верхних чисел сечения.

Def. Два сечения считаются равными, если они тождественно равны как множества. Сечение А считается меньше сечения С, A<C, если найдётся рС, рА.

Пусть А,С – сечения. Пишем AC, если А=С или A<C. A>C означает попросту, что С<А. Сечение, соответствующее рациональному числу r обозначим звёздочкой: r*. Положительными сечениями назовём такие сечения А, что А>0*. Соответственно вводятся неотрицательные, отрицательные и неположительные сечения.

Упражнение 11. Для любых двух сечений А и С выполняется и при том только одно из трёх отношений: А=С; A<C или A>C.

Следующее упражнение, вкупе с предшествующим, показывает, что введённое отношение порядка во множестве сечений превращает его в линейно упорядоченное множество:

Упражнение 12. Для любых трёх сечений А, В и С (А<B)(B<C)A<C.

Переходим к построению арифметике во множестве сечений.

Упражнение 13. Пусть А и В – сечения. Тогда С={cQ, c=a+b aA, bB} – сечение.

Т.о., корректно определено сложение сечений.

Упражнение 14.

Сложение сечений коммутативно, ассоциативно и 0* служит нейтральным элементом.

Следующее упражнение служит подготовительным к упр. 16:

Упражнение 15.

Пусть заданы сечение А и положительное рациональное число c. Докажите, что aA и bB (B-множество верхних чисел сечения А), причём b не является наименьшим из чисел В, такие, что b-a=c.

Упражнение 16. Каждое сечение имеет обратный по сложению элемент. Т.о., множество сечений по сложению образует абелеву группу.

Следующее упражнение показывает, что операция сложения сечений согласована с отношением порядка, введённым ранее.

Упражнение 17. Для сечений (А<B)  (A+C) < (B+C)

Определим сначала произведение для неотрицательных сечений:

Упражнение 18. Пусть А0*, В0*, С={Q^-{c=ab, a0, aA; b0, bB}}. Тогда С – сечение.

Оно и называется произведением сечений А и В, С=АВ.

Так же, как и прежде, вводится функция «абсолютная величина» и с её помощью доопределяется умножение сечений в оставшихся случаях.

Def.

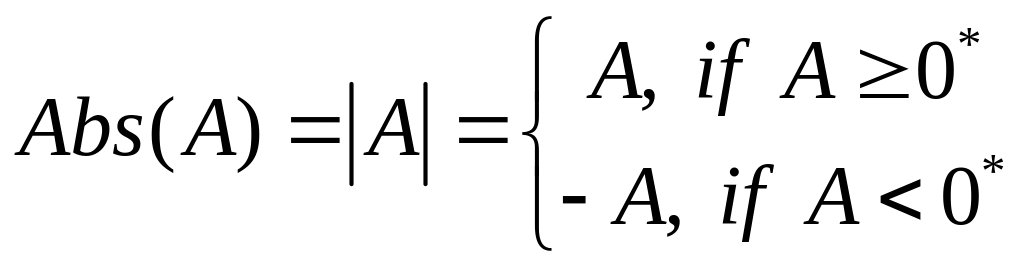
Упражнение 19.  A A0* и A=0*А=0*.

Def. Пусть теперь А и В – любые сечения. Определим их произведение: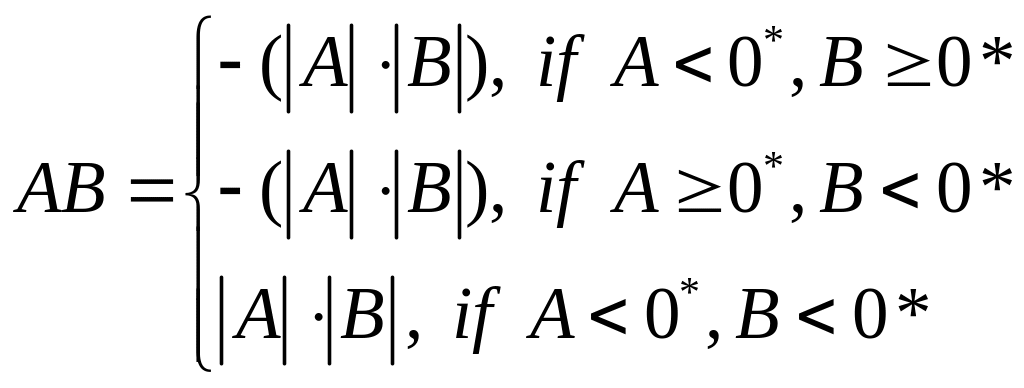

Упражнение 20.

1. Относительно введённых операций множество сечений образует поле с нейтральным элементом по умножению, равным 1*.

2. Операция умножения также согласована с отношением порядка, а именно: (A<B) (C>0*) (AC<BC).

Упражнение 21. Подполе рациональных сечений Q* и поле рациональных чисел Q изоморфны как (линейно) упорядоченные поля.

Осталось переименовать сечения в числа – и вся процедура закончена. Рациональные сечения назвать рациональными числами, остальные – иррациональными. Все вместе называются действительными (вещественными) числами.

Хотя множество Q рациональных чисел счётно, а множество R действительных – несчётно, тем не менее, и для действительных чисел имеет место утверждение:

Упражнение 22. Между любыми двумя действительными числами найдётся рациональное число.